билеты. билеты 28-42. Задача нахождения критического пути в графе Задача нахождения критического, (т е. длиннейшего) пути в графе это задача, связанная с загрузкой станочного оборудования, сборки многозвенных изделий и т д

• Название: Задача нахождения критического пути в графе Задача нахождения критического, (т е. длиннейшего) пути в графе это задача, связанная с загрузкой станочного оборудования, сборки многозвенных изделий и т д
• Анкор: билеты
• Дата: 17.05.2022
• Размер: 0.51 Mb.
• Имя файла: билеты 28-42.docx
• Тип: Задача; #534611

28. Задача нахождения критического пути в графе Задача нахождения критического, (т. е. длиннейшего) пути в графе ― это задача, связанная с загрузкой станочного оборудования, сборки многозвенных изделий и т. д. Алгоритм Дейкстры Алгоритм находит кратчайшее расстояние от одной из вершин графа до всех остальных и работает только для графов без ребер отрицательного веса.

Шаг 1. Всем вершинам, за исключением первой, присваивается вес равный бесконечности, а первой вершине – 0.
Шаг 2. Все вершины не выделены.
Шаг 3. Первая вершина объявляется текущей.
Шаг 4. Вес всех невыделенных вершин пересчитывается по формуле: вес невыделенной вершины есть минимальное число из старого веса данной вершины, суммы веса текущей вершины и веса ребра, соединяющего текущую вершину с невыделенной.
Шаг 5. Среди невыделенных вершин ищется вершина с минимальным весом. Если таковая не найдена, то есть вес всех вершин равен бесконечности, то маршрут не существует. Следовательно, выход. Иначе, текущей становится найденная вершина. Она же выделяется.
Шаг 6. Если текущей вершиной оказывается конечная, то путь найден, и его вес есть вес конечной вершины. Шаг 7. Переход на шаг 4.

29. Потоком в сети S называется пара, составленная из числовой и нечисловой функций (f, w): w – ориентация всех неориентированных ребер сети, f =f(e) – функция значений потока на ребрах. Один из способов поиска максимального потока — метод Форда-Фалкерсона:

1. 
   Положим начальный поток равным нулю.
   
2. 
   Пока есть простой путь из истока в сток, по которому можно еще пустить поток, дополняем поток по этому пути.
   
   
   

Наиболее эффективной реализацией метода Форда-Фалкерсона является алгоритм Эдмондса-Карпа, суть которого состоит в том, что поиск пути выполняется обходом дерева в ширину.

30. Сетевой график – необходимый элемент сложного производства, состоящего из нескольких связанных и зависящих друг от друга этапов. Выявление критического пути и временных резервов производства – основная задача, решаемая построением сетевого графика. К основным параметрам сетевого графика относятся: - критический путь - резервы времени свершения событий - резервы времени для выполнения работ.

31. Правила построения сетевых графиков

1. Завершающее событие лишь одно.

2. Исходное событие лишь одно.

3. Любые два события должны быть непосредственно связаны стрелкой не более чем одной работой. Если два события связаны более чем одной работой, рекомендуется ввести дополнительное событие и фиктивную работу

4. В сети не должно быть замкнутых циклов.

5. Если для выполнения одной из работ необходимо получить результаты всех работ, входящих в предшествующее для нее событие, а для другой работы достаточно получить результат нескольких из этих работ, то нужно ввести дополнительное событие, отражающее результаты только этих последних работ, и фиктивную работу, связывающую новое событие с прежним. Ранний срок t_p(j) свершения события Правило вычисления:



Поздний срок: 

Резерв времени

Критические события резервов не имеют. Самый продолжительный путь сетевого графика от исходного события к завершающему называется критическим.

Резерв: Полный резерв времени, Свободный резерв времени

32. Высказыванием называется повествовательное предложение, о котором можно судить, является ли оно истинным или ложным. Суждение - это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком, отношения между предметами или факт существования предмета. Суждения могут быть либо истинными, либо ложными.

33. 1. Отрицанием высказывания А называется высказывание ͞А, которое принимает значение «истина», если А ложно, и принимает значение «ложь», если А истинно.
2. Конъюнкцией (логическим умножением) высказываний А и В называется высказывание А˄В (А&В), которое принимает значение «истина» только в том случае, если оба высказывания А и В истинные.
3. Дизъюнкцией (логическим сложением) высказываний А и В называется высказывание А˅В (А+В), которое принимает значение «ложь» только в том случае, если оба высказывания А и В ложные.
4. Импликацией (логическим следованием) высказываний А и В называется высказывание А→В, которое принимает значение «ложь» только в том случае, если А истинно и В ложно.
5. Эквиваленцией (логической равносильностью) высказываний А и В называется высказывание А↔В, которое принимает значение «истина» только в том случае, если А и В принимают одинаковые значения.
6. Штрихом Шеффера (или антиконъюнкцией) высказываний А и В называется высказывание А|В, которое принимает значение «ложь» только в том случае, если оба высказывания А и В принимают значения «истина».
7. Стрелкой Пирса (или антидизъюнкцией) высказываний А и В называется высказывание А↓В, которое принимает значение «истина» только в том случае, если оба высказывания А и В принимают значения «ложь».
8. Сложением по модулю 2 (или суммой Жегалкина) высказываний А и В называется высказывание АВ, которое принимает значение «ложь» только в том случае, если оба высказывания А и В принимают одинаковые значения.

34. Для любых формул X, Y, Z справедливы следующие равносильности (законы алгебры высказываний):

1.   ,   (коммутативность);

2.   ,   (ассоциативность);

3.   ,   (дистрибутивность);

4.   ,   (идемпотентность);

5.   ,   (з-ны поглощения);

6.   (закон двойного отрицания);

7.   ,   (законы де Моргана);

8.   ,   ,   ,   ,   ,   (законы, определяющие действия с константами);

9.   ,   (исключение импликации и эквиваленции);

10.   (исключение дизъюнкции);

11.   (исключение конъюнкции).

35. Высказывания называются эквивалентными, если соответствующие значения каждого из них совпадают в таблице истинности.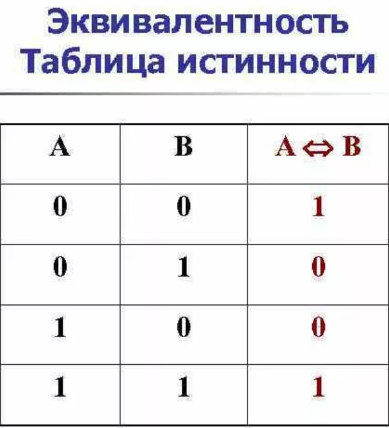

36. В алгебре логики имеется четыре основных закона:

1. Переместительный, или закон коммутативности для операций сложения и умножения, соответственно:

A Ú B = B Ú A;

A B = B A.

2. Сочетательный, или закон ассоциативности для сложения и умножения, соответственно:

(A Ú B) Ú C = A Ú (B Ú C);

(A B) C = A (B C).

3. Распределительный, или закон дистрибутивности для сложения и умножения, соответственно:

(A Ú B) C = A C Ú B·C;

(A B) Ú C = (A Ú C) (B Ú C).

4. Закон двойственности или инверсии (правило де Моргана) для логических операций сложения и умножения, соответственно:

сложение   ,   ,   , 

умножение   ,   ,   ,   .

37. Понятие– это форма мышления, посредством которой отражаются общие и существенные признаки предмета или определённого класса предметов и присущих ему свойств.

38. булева функция – это функция, и аргументы и значение которой принадлежит множеству { 0, 1 }.

x1	x2	...	xn-1	xn	f
0	0	...	0	0	f(0,0,...,0,0)
0	0	...	0	1	f(0,0,...,0,1)
0	0	...	1	0	f(0,0,...,1,0)
0	0	...	1	1	f(0,0,...,1,1)
...	...	...	...	...	...
1	1	...	0	0	f(1,1,...,0,0)
1	1	...	0	1	f(1,1,...,0,1)
1	1	...	1	0	f(1,1,...,1,0)
1	1	...	1	1	f(1,1,...,1,1)

39. Формула А от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:

1) А является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных, причем на i-м месте этой конъюнкции стоит либо переменная, либо ее отрицание;

2) все элементарные конъюнкции в такой ДНФ попарно различны.

Формула А от k переменных называется совершенной конъюнктивной нормальной формой (СКНФ), если:

1) А является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных, причем на i-м месте этой дизъюнкции стоит либо переменная х, либо ее отрицание;

2) все элементарные дизъюнкции в такой КНФ попарно различны.

40. Систему булевых функций называют полной, если любая булева функция может быть выражена в виде формулы над этой системой 
Теорема (Поста): система булевых функций полна тогда и только тогда, когда она целиком не лежит ни в одном из классов Поста.
Теорема 4.1 (И.И. Жегалкина). Каждая функция f (x1,...,xn) ∈ P2 может быть единственным образом представлена в виде полинома Жегалкина Pf .
Построение многочлена Жегалкина по таблице истинности функции. В этом случае столбец значений булевой функции выписывается в строку. Под ней формируется строка, значения которой являются суммой по модулю 2 двух ближайших значений предыдущей строки. Остальные строки формируются по тому же принципу. Последняя строка будет состоять из единственного значения, а вся таблица будет иметь вид равнобедренного треугольника. Многочлен Жегалкина составляется из тех слагаемых, в чьих строках имеется единица на левом боковом ребре треугольника, а каждое слагаемое является конъюнкцией тех переменных, в чьих позициях в данной строке таблицы истинности стоят единицы. Нулевому набору значений соответствует слагаемое 1.

41. Упрощение выражений булевых функций (минимизация) основывается на понятии несущественности переменных. Переменная называется несущественной на паре наборов, если при изменении ее значения на противоположное булева функция сохраняет свое значение.

42. Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.