эйлеров цикл курс. Задача о кёнигсбергских мостах
 Скачать 195.13 Kb. Скачать 195.13 Kb.
|
|
Содержание Введение 2 1Теоретическая часть 3 2Программная реализация работы 10 2.1Среда разработки и организация решения 10 2.2Программная реализации Эйлерова цикла 13 3Результат выполнения программы 17 Заключение 19 Список рекомендуемой литературы 21 ВведениеПервая работа по теории графов, принадлежащая известному швейцарскому математику Л.Эйлеру, появилась в 1736г. Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики и особенно её приложений дало сильный толчок развитию теории графов. Уже в XIX столетии графы использовались при построении схем. В настоящее время эта теория находит многочисленное применение в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сети нефтепроводов, в программировании и теории игр, теории передачи сообщений. Теория графов теперь применяется и в таких областях, как экономика, психология и биология.
Задача о кёнигсбергских мостах. Отцом теории графов является Эйлер (1707-1782), решивший в 1736г. широко известную в то время задачу, называвшуюся проблемой Кёнигсбергских мостов. В городе Кёнигсберге (ныне Калининград) было два острова, соединенных семью мостами с берегами реки Преголя и друг с другом так, как показано на рисунке 5. Задача состояла в следующем: найти маршрут прохождения всех четырёх частей суши, который начинался бы с любой из них, кончался бы на этой же части и ровно один раз проходил по каждому мосту. 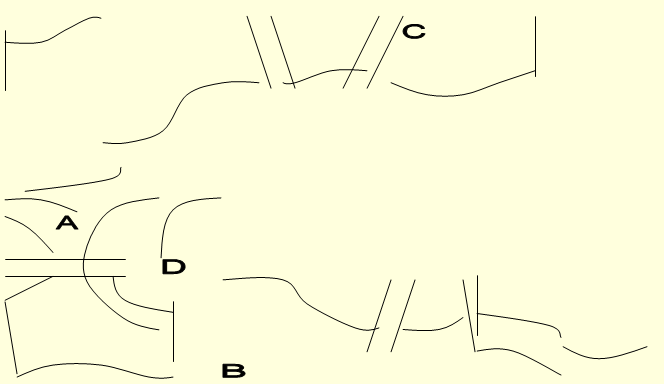 Рис.1. Легко, конечно попытаться решить эту задачу эмпирически, производя перебор всех маршрутов, но все попытки окончатся неудачей. Исключительный вклад Эйлера в решение этой задачи заключается в том, что он доказал невозможность такого маршрута. Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а каждый мост – линией (ребром), соединяющей соответствующие точки. Получился “граф”. Этот граф показан на рисунке 6, где точки отмечены теми же буквами, что и четыре части суши на рисунке 5. 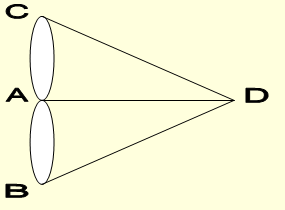
Рис.2. Утверждение о не существовании “положительного” решения у этой задачи эквивалентно утверждению о невозможности обойти специальным образом граф, представленный на рисунке 6. Отправляясь от этого частного случая Эйлер обобщил постановку задачи и нашёл критерий существования обхода у данного графа, а именно граф должен быть связным и каждая его вершина должна быть инцидентна чётному числу рёбер. Эйлеровы графы Решение Эйлером задачи о Кёнигсбергских мостах привела к первой опубликованной работе по теории графов. Задачу об обходе мостов можно обобщить и получить следующую задачу теории графов: можно ли найти в данном графе G цикл, содержащий все вершины и все рёбра? Граф, в котором это возможно, называется эйлеровым. Таким образом, эйлеров граф имеет эйлеров цикл – замкнутую цепь, содержащую все вершины и все рёбра. Ясно, что эйлеров граф должен быть связным. Если снять ограничения на замкнутость цепи, то граф называется полуэйлеровым. Определение 1. Эйлеровой цепью в неориентированном графе G называется простая цепь, содержащая все ребра графа G. Эйлеровым циклом назы вается замкнутая Эйлерова цепь. Аналогично, эйлеров путь в орграфе G — это простой путь, содержащий все дуги графа G. Эйлеров контур в орграфе G — это замкнутый эйлеров путь. Граф, в котором существует эйлеров цикл, называется эйлеровым . Простой критерий существования эйлерова цикла в связном графе дается следующей теоремой. Теорема 1. (Эйлер) Эйлеров цикл в связном неориентированном графе G (X, E ) существует только тогда, когда все его вершины имеют четную степень. Доказательство. Необходимость. Пусть m — эйлеров цикл в связном гра фе G, x — произвольная вершина этого графа. Через вершину x эйлеров цикл проходит некоторое количество k (k ³1) раз, причем каждое прохождение, очевидно, включает два ребра, и степень этой вершины равна 2k, т.е. четна, так как x выбрана произвольно, то все вершины в графе G имеют четную сте пень. Достаточность. Воспользуемся индукцией по числу mребер графа. Эйле ровы циклы для обычных (не псевдо) графов можно построить начиная с m =3.Легко проверить, что единственный граф с m =3, имеющий все вершины с четными степенями, есть граф K 3 (рис. 2). Существование эйлерова цикла в нем очевидно. Таким образом, для m =3 достаточность условий доказываемой теоремы имеет место. Пусть теперь граф G имеет m >3 ребер, и пусть утверждение справедливо для всех связных графов, имеющих меньше, чем m ребер. Зафиксируем произвольную вершину a графа G и будем искать простой цикл, идущий из a в a. Пусть m(a, x ) — простая цепь, иду щая из a в некоторую вершину x. Если x¹a, то цепь m можно продолжить из вершины x в некотором направлении. Через некоторое число таких про дол же ний мы придем в вершину z ÎX, из которой нельзя продлить полу чен ную про стую цепь. Легко видеть, что z = a так как из всех остальных вершин цепь может выйти (четные степени!); a в a она начиналась. Таким образом, нами построен цикл m, идущий из a в a. Предположим, что построенный про стой цикл не содержит всех ребер графа G. Удалим ребра, входящие в цикл m, из графа G и рассмотрим полученный граф . В графе все вершины имеют четные степени. Пусть — компо нен ты связ нос ти графа , содержащие хотя бы по одному ребру. Соглас но пред поло же нию индукции все эти компоненты обладают эйлеровыми циклами m1, m1, …, mk соот вет ствен но. Так как граф G связан, то цепь m встре чает каждую из компонент. Пусть первые встречи цикла m с ком понентами происходят соответственно в вершинах x 1, x 2, …, xk. Тогда про стая цепь n(a, a )=m(a, x 1 ) Um1 (x 1, x 1 ) Um(x 1, x 2 ) U…Umk (xk, xk ) Um(xk, a ) является эйлеровым циклом в графе G. Теорема доказана. Замечание. Очевидно, что приведенное доказательство будет верно и для псевдографов, содержащих петли и кратные ребра (см. рис. 1, а). Таким образом, задача о кенигсбергских мостах не имеет ре ше ния, так как соответствующий граф (см. рис. 1, б) не имеет эйлерова цикла из-за не четности степеней все вершин. Отметим, что из существования эйле ро ва цикла в неориентированном графе G не следует связность этого графа. Напри мер, неориентированный граф G на рис. 3 обладает эйлеровым циклом и вместе с тем несвязен. Совершенно также, как теорема 1, могут быть доказаны следующие два утверждения. Теорема 2. Связный неориентированный граф Gобладает эйлеровой цепью тогда и только тогда, когда число вершин нечетной степени в нем равно 0 или 2, причем если это число равно нулю, то эйлерова цепь будет являться и циклом. Можно также обобщить задачу, которую решал Эйлер следующим обра зом. Будем говорить что множество не пересекающихся по ребрам простых цепей графа Gпокрывает его, если все ребра графа G включены в цепи mi. Нужно найти наименьшее количество таких цепей, которыми можно покрыть заданный граф G . Если граф G — эйлеров, то очевидно, что это число равно 1. Пусть теперь G не является эйлеровым графом. Обозначим через k число его вер шин нечетной степени. По теореме … k четно. Очевидно, что каждая верши на нечетной степени должна быть концом хотя бы одной из покрывающих G цепей mi. Следовательно, таких цепей будет не менее чем k /2. С другой сто роны, таким количеством цепей граф G покрыть можно. Чтобы убедиться в этом, расширим G до нового графа , добавив k /2 ребер , соединяющих раз личные пары вершин нечетной степени. Тогда оказывается эйлеровым графом и имеет эйлеров цикл . После удаления из ребер граф разло жится на k /2 цепей, покрывающих G. Таким образом, доказана. Алгоритм построения эйлерова цикла Для начала отметим, что теорема 1 также дает метод построения эйлерова цикла. Здесь мы рассмотрим несколько иной алгоритм. Пусть G (X, E ) — связный неорентированный граф, не имеющий вершин нечетной степени. Назовем мостом такое ребро, удаление которого из связного графа разбивает этот граф на две компоненты связности, имеющие хотя бы по одному ребру. 1°. Пусть a — произвольная вершина графа G. Возьмем любое ребро e 1 =(a, x 1 ), инцидентное вершине a, и положим m = {e 1 }. 2°. Рассмотрим подграф G 1 (X, E\ m1 ). Возьмем в качестве e 2 ребро, инци дентное вершине x 1 и неинцидентное вершине a, которое также не является мостом в подграфе G 1 (если такое ребро e 2 существует!). Получим простую цепь m2 = {e 1, e 2 }. 3°. Пусть e 2 = (x 1, x 2 ), x ¹a. Рассмотрим подграф G 2 (X, E\m2 ) и удалим из него все изо лированные вер шины. В полученном подграфе выберем ребро e 3 ÎE \ m2, инцидентное вершине a, которое не является мостом в под графе (если такое ребро e 3 суще ству ет!). Получим простую цепь m3 = {e 1, e 2, e 3 }. Продолжая указанный процесс, мы через конечное число шагов получим эйлеров цикл m = {e 1, e 2, …, en }, где n — число ребер графа G (X, E ). Обоснование алгоритма Предположим, что уже построена простая цепь mk -1 = {e1, e 2, …, ek -1 } для k ³2 методом, указанным в алгоритме. Пусть ek -1 = (xk -2, xk -1 ) и xk -1 ¹a. Рас смо трим подграф , который получается из подграфа G k -1 (X, E\ mk -1 ) удалением всех изолированных вершин. Вершина xk -1 в этом подграфе имеет нечет ную степень, поэтому существует по крайней мере одно ребро ek ÎE\ mk -1, ин ци дентное xk -1. Если это ребро единственное, то оно не является мостом в графе . В противном случае вершина aбудет связана с некоторой вер ши ной единственной цепью, содержащей ребро ek, что противоречит суще ствованию эйлерова цикла в графе G. Поскольку ek — не мост, то процесс мож но продолжать, взяв . Если ребро ekне единственное инци дентное вершине xk -1, то среди этих ребер есть по крайней мере одно, не явля ющееся мостом. В противном случае один из этих мостов можно выбро сить так, что вершины xk -1 и a попадут в разные компоненты связности графа . Если xk -1 принадлежит компоненте M, то в этой компоненте все вер шины имеют четную степень, поэтому существует эйлеров цикл в M, про хо дящий через xk -1. Этот цикл содержит все ребра, инцидентные xk -1 и при над лежащие , являющиеся одновременно мостами. Получено противоречие, так как ребра из эйлерова цикла мостами быть не могут. Из предыдущего следует, что процесс нельзя продолжать тогда и только тогда, когда мы попадем в вершину a, причем степень вершины a относительно непройденных ребер равна нулю. Докажем, что в этом случае построенный цикл m — простой цикл. Покажем, что m содержит все ребра графа G. Если не все ребра графа Gпринадлежат m, то не принадлежащие m ребра порождают компоненты связности C 1, …, Cm (m ³1) в подграфе . Пусть компонента Ci, 1£i £m соединяется с циклом m в вершине yi. Если существует ребро e Îm, такое, что e =(yi, a ), то при построении цикла m было нарушено правило выбора ребра e, что невозможно. Если часть цикла m, соединяющая yi и a, состоит более чем из одного ребра, то первое ребро этой части было мостом, и поэтому было нарушено правило вы бора , что невозможно. Итак, непройденных ребер быть не может, поэ тому m — эйлеров цикл.
Представленная курсовая работа предназначена для разработки программы на языке программирования C++, которая ищет и выводит эйлеров цикл или путь в графе. Основной задачей этого курсового проекта является программная реализация на языке программирования C++, благодаря которой пользователь имеет возможность вывести заданный граф по Эйлерову циклу и получить ответ в виде маршрута по вершинам графа. Реализация программы на компьютере позволит произвести моментальный вывод результатов.
Курсовая работа выполнена в интегрированной среде программирования MS Visual Studio 2017. Microsoft Visual Studio - это программная средапоразработке приложений для ОС Windows, как консольных, так и с графическим интерфейсом. В комплект входят следующие основные компоненты: 1. Visual Basic.NET - для разработки приложений на VisualBasic; 2. Visual C++ - на традиционном языке C++; 3. Visual C# - наязыке C# (Microsoft); 4. Visual F# - на F# (Microsoft Developer Division). Функциональная структура среды включает в себя: 1)редактор исходного кода, который включает множество дополнительных функций, как автодополнение IntelliSense, рефракторинг кода и т. д.; 2)отладчик кода; 3)редактор форм, предназначенный для упрощённого конструирования графических интерфейсов; 4)веб-редактор; 5)дизайнер классов; 6)дизайнерсхем баз данных. Visual Studio также позволяет создавать и подключать сторонние дополнения (плагины) для расширения функциональности практически на каждом уровне, включая добавление поддержки систем контроля версий исходного кода (Subversion и VisualSourceSafe), добавление новых наборов инструментов (для редактирования и визуального проектирования кода на предметно-ориентированных языках программирования или инструментов для прочих аспектов процесса разработки программного обеспечения). Коммерческие версии в порядке возрастания цены: Visual Studio Professional, Visual Studio Premium и Visual Studio Ultimate. Достоинства и недостатки Интегрированная среда разработки (IntegratedDevelopmentEnvironment - IDE) Visual Studio предлагает ряд высокоуровневых функциональных возможностей, которые выходят за рамки базового управления кодом. Ниже перечислены основные преимущества IDE-среды Visual Studio. Встроенный Web-сервер. Для обслуживания Web-приложения ASP.NET необходим Web-сервер, который будет ожидать Web-запросы и обрабатывать соответствующие страницы. Наличие в Visual Studio интегрированного Web-сервера позволяет запускать Web-сайт прямо из среды проектирования, а также повышает безопасность, исключая вероятность получения доступа к тестовомуWeb-сайту с какого-нибудь внешнего компьютера, поскольку тестовый сервер может принимать соединения только с локального компьютера. Поддержка множества языков при разработке. Visual Studio позволяет писать код на своем языке или любых других предпочитаемых языках, используя все время один и тот же интерфейс (IDE). Более того, Visual Studio также еще позволяет создавать Web-страницы на разных языках, но помещать их все в одно и то же Web-приложение. Единственным ограничением является то, что в каждой Web-странице можно использовать только какой-то один язык (очевидно, что в противном случае проблем при компиляции было бы просто не избежать). Меньше кода для написания. Для создания большинства приложений требуется приличное количество стандартного стереотипного кода, и Web-страницы ASP. NET тому не исключение. Например, добавление Web-элемента управления, присоединение обработчиков событий и корректировка форматирования требует установки в разметке страницы ряда деталей. В Visual Studio такие детали устанавливаются автоматически. Интуитивный стиль кодирования. По умолчанию Visual Studio форматирует код по мере его ввода, автоматически вставляя необходимые отступы и применяя цветовое кодирование для выделения элементов типа комментариев. Такие незначительные отличия делают код более удобным для чтения и менее подверженным ошибкам. Применяемые Visual Studio автоматически параметры форматирования можно даже настраивать, что очень удобно в случаях, когда разработчик предпочитает другой стиль размещения скобок (например, стиль K&R, при котором открывающая скобка размещается на той же строке, что и объявление, которому она предшествует). Более высокая скорость разработки. Многие из функциональных возможностей Visual Studio направлены на то, чтобы помогать разработчику делать свою работу как можно быстрее. Удобные функции, вроде функции IntelliSense (которая умеет перехватывать ошибки и предлагать правильные варианты), функции поиска и замены (которая позволяет отыскивать ключевые слова как в одном файле, так и во всем проекте) и функции автоматического добавления и удаления комментариев (которая может временно скрывать блоки кода), позволяют разработчику работать быстро и эффективно. Возможности отладки. Предлагаемые в Visual Studio инструменты отладки являются наилучшим средством для отслеживания загадочных ошибок и диагностирования странного поведения. Разработчик может выполнять свой код по строке за раз, устанавливать интеллектуальные точки прерывания, при желании сохраняя их для использования в будущем, и в любое время просматривать текущую информацию из памяти. Visual Studio также имеет и множество других функций: возможность управления проектом; встроенная функция управления исходным кодом; возможность рефакторизации кода; мощная модель расширяемости. Более того, в случае использования Visual Studio 2008 Team System разработчик получает расширенные возможности для модульного тестирования, совместной работы и управления версиями кода (что значительно больше того, что предлагается в более простых инструментах вроде Visual SourceSafe). В качестве недостатка можно отметить невозможность отладчика (Microsoft Visual Studio Debugger) отслеживать в коде режима ядра. Отладка в Windows в режиме ядра в общем случае выполняется при использовании WinDbg, KD или SoftICE. Данная программа выполняет алгоритм Дейкстры, с помощью интерфейса Windows Form пользователю будет предложено ввестиколичество вершинграфа. Далее задание вершинам дуг и их расстояний, а также вершину от которой будет проводится расчет минимальных расстояний до всех остальных вершин, после чего будет выведен результат работы алгоритма.
#include #include struct Node { int inf; Node *next; }; //============================Stack============================== void push(Node *&st,int dat) { // Загрузка числа в стек Node *el = new Node; el->inf = dat; el->next = st; st=el; } int pop(Node *&st) { // Извлечение из стека int value = st->inf; Node *temp = st; st = st->next; delete temp; return value; } int peek(Node *st) { // Получение числа без его извлечения return st->inf; } //============================================================== Node **graph; // Массив списков смежности const int vertex = 1; // Первая вершина FILE* fi = fopen("e_graph.txt","r"); //Файл с матрицей смежности FILE* fo = fopen("e_cycle.txt","w"); // Результирующий файл void add(Node*& list,int data) { //Добавление смежной вершины if(!list){list=new Node;list->inf=data;list->next=0;return;} Node *temp=list; while(temp->next) temp=temp->next; Node *elem=new Node; elem->inf=data; elem->next=NULL; temp->next=elem; } void del(Node* &l,int key) { // Удаление вершины key из списка if(l->inf==key) {Node *tmp=l; l=l->next; delete tmp;} else { Node *tmp=l; while(tmp) { if(tmp->next) // есть следующая вершина if(tmp->next->inf==key) { // и она искомая Node *tmp2=tmp->next; tmp->next=tmp->next->next; delete tmp2; } tmp=tmp->next; } } } int eiler(Node **gr,int num) { // Определение эйлеровости графа int count; for(int i=0;i { //проходим все вершины count=0; Node *tmp=gr[i]; while(tmp) { // считаем степень count++; tmp=tmp->next; } if(count%2==1)return 0; // степень нечетная } return 1; // все степени четные } void eiler_path(Node **gr) { //Построение цикла Node *S = NULL;// Стек для пройденных вершин int v=vertex;// 1я вершина (произвольная) int u; push(S,v); //сохраняем ее в стек while(S) { //пока стек не пуст v = peek(S); // текущая вершина if(!gr[v]){ // если нет инцидентных ребер v=pop(S); fprintf(fo,"%d ",v); //выводим вершину } else { u=gr[v]->inf; push(S,u); //проходим в следующую вершину del(gr[v],u); del(gr[u],v); //удаляем пройденное ребро } } } int main() { int n; // Количество вершин int zn;// Текущее значение fscanf(fi,"%d",&n); graph=new Node*[n]; for(int i=0;i for(int i=0;i for(int j=0;j { fscanf(fi,"%d",&zn); if(zn) add(graph[i],j); } if(eiler(graph,n))eiler_path(graph); else fprintf(fo,"Граф не является эйлеровым."); return(0); }
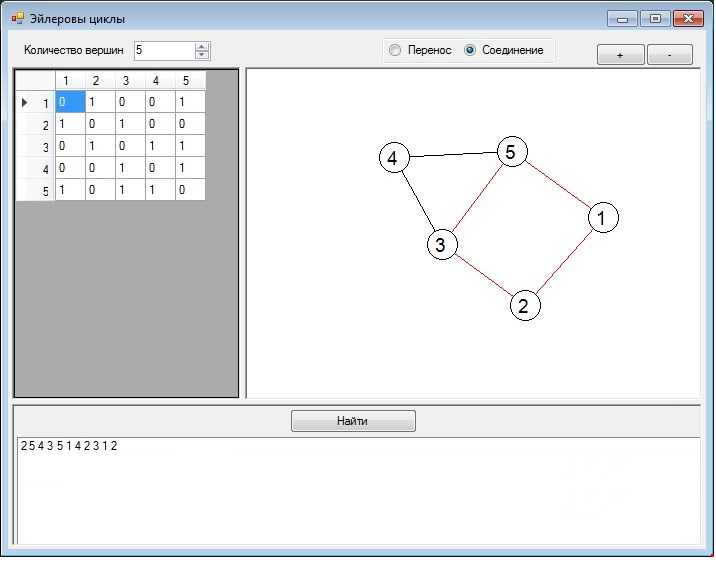 Рис.3. 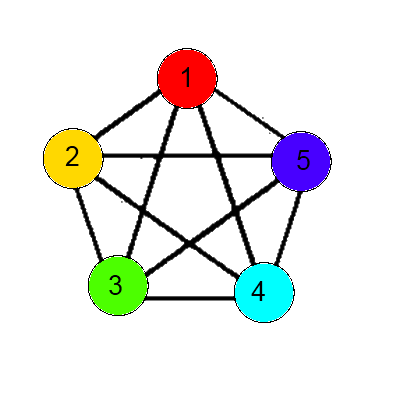 Рис.4. Матрица смежности для этого графа: 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 Результат выполнения программы - это маршрут по вершинам графа, причем посещаются все ребра графа, но при этом каждое из ребер посещается только однажды. 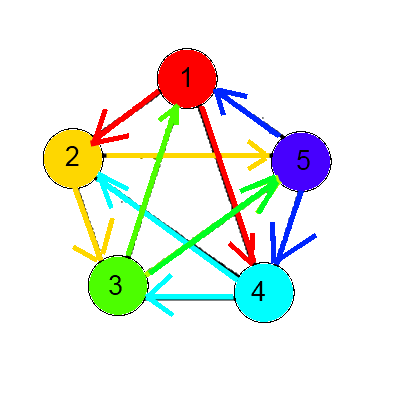 Рис.5. ЗаключениеИтогом данной курсовой работы является программа, реализованная на языке C ++, которая ищет и выводит эйлеров цикл или путь в графе. В качестве возможностей развития программы являются такие нереализованные функции, как отображение заданного графа или улучшение интерфейса программы для задания графа визуальным способом при помощи элементов вершин и ребер, а также оптимизация программного кода для увеличения работоспособности. Список рекомендуемой литературы
|
