Задача о нахождении кратчайших путей в графе
 Скачать 7.05 Mb. Скачать 7.05 Mb.
|
|
Занятие 7. Методы хранения графов в памяти ЭВМ. Задача о нахождении кратчайших путей в графе. Методы хранения графов в памяти ЭВМ Графом G(V, Е) называется совокупность двух множеств — непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элементов множества V (Е — множество ребер).  Соединения между узлами графа называются ребрами. Если узлы графа не нумерованы, то ребра являются неориентированными. У графа с нумерованными узлами ребра ориентированы. Ребрам могут быть присвоены определенные веса или метки. Смежность Если ребро соединяет 2 вершины, то говорят, что оно им инцидентно; Смежные вершины - вершины, соединенные ребром. 2 вершины, соединенные ребром, могут совпадать; такое ребро называется петлей. Степень вершины - число ребер, инцидентных вершине. Если степень вершины равна 0, то получается изолированная графа. Кратные вершины - если 2 ребра инцидентны одной и той же паре вершин. Мультиграф - граф, содержащий кратные ребра. Другие определения Если элементами множества Е являются упорядоченные пары, то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества E — дугами. Если элементом множества E может быть пара одинаковых (не различных) элементов V, то такой элемент множества E называется петлей, а граф называется графом с петлями (или псевдографом). Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом. Если элементами множества Е являются не обязательно двухэлементные, любые подмножества множества V, то такие элементы множества Е называются гипердугами, а граф называется гиперграфом. Если задана функция Е:V —> Ми/или F:Е—> М, то множество М называется множеством пометок, а граф называется помеченным (или нагруженным).В качестве множества пометок обычно используются буквы или целые числа. Виды графов и операции над ними   Виды графов и операции над ними Тривиальные и полные графы Граф, состоящий из одной вершины, называется тривиальным. Граф, состоящий из простого цикла с к вершинами, обозначается Ск. Пример С3 — треугольник. Граф, в котором каждая пара вершин смежна, называется полным. Полный граф с р вершинами обозначается Кр, он имеет максимально возможное число ребер: Полный подграф (некоторого графа) называется кликой (этого графа). Двудольные графы  Представление графов в ЭВМ Конструирование структур данных для представления в программе объектов математической модели — это основа искусства практического программирования. Используется четыре различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных представлений, общее число которых необозримо. Требования к представлению графов Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены четыре наиболее часто используемых представления с указанием характеристики n(р, q) — объема памяти для каждого представления. Здесь р - число верпин, а q - число ребер. Указанные представления пригодны для графов и орграфов, а после некоторой модификации также и для псевдографов, мультиграфов и гиперграфов.   Задача о нахождении кратчайших путей в графе Примеры: 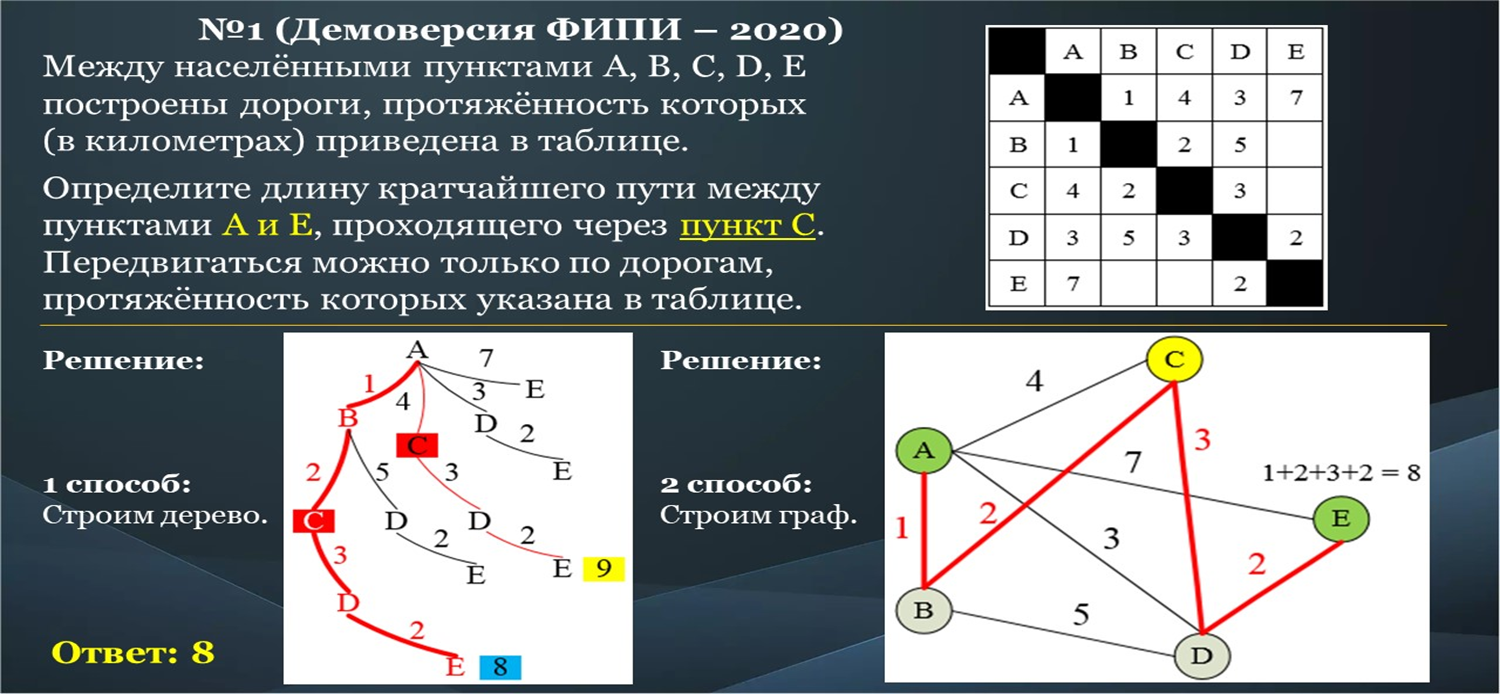 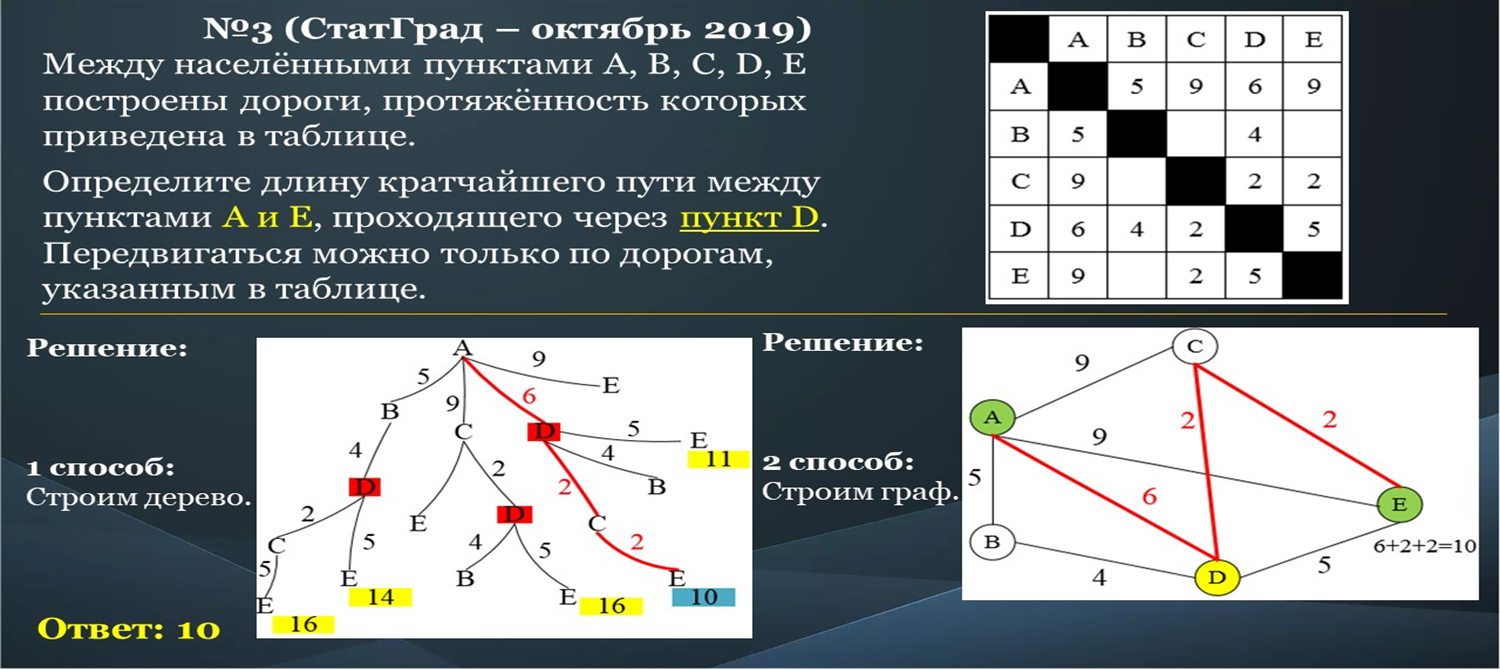 |
