Задание 4_матрицы. Задача обхода матрицы по заданному маршруту может возникнуть при решении различных задач
 Скачать 141.24 Kb. Скачать 141.24 Kb.
|
|
Задание 4. обход матриц Задача обхода матрицы по заданному маршруту может возникнуть при решении различных задач. Возможны следующие варианты обхода матриц: а) по столбцам или строкам; б) по диагоналям; б) змейкой по строкам или столбцам; в) змейкой по диагоналям; г) по разворачивающимся или сворачивающимся спиралям; д) другие варианты. Возможные схемы обхода матриц приведены в заданиях. Их количество легко можно увеличить, если использовать различные повороты на 90, 180 и 270 градусов. Для реализации различных схем обхода необходимы навыки работы с индексами элементов. Пример 1. П  роизвести обход элементов матрицы по маршруту, приведенному на рис.1. роизвести обход элементов матрицы по маршруту, приведенному на рис.1. Исходя из заданной схемы нам необходимо пройтись по всем строкам матрицы, начиная с первой. Этот обход организуется с помощью внешнего цикла. Внутри этого цикла должен быть организован цикл по столбцам. При этом, в зависимости от четности или нечетности строки, проход по столбцам происходит либо начиная с первого и кончая последним, либо наоборот. 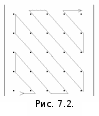 Пример 2. Произвести обход матрицы по маршруту, приведенному на рис.2. Если присмотреться к матрице, то можно увидеть, что эта схема обхода аналогична обходу по строкам (или столбцам), но повернута на 45 градусов. Здесь вместо строк обход происходит по диагоналям, параллельным главной диагонали. Нетрудно определить, что количество диагоналей (k) равно (2n-1). Таким образом для обхода всех диагоналей, также как и в программе 7.4, должен быть организован внешний цикл по k от 1 до (2n-1). В качестве первой диагонали должна быть взята самая нижняя. Внутренний цикл по столбцам, в зависимости от четности диагонали должен быть либо возрастающим (от 1 до n), либо убывающим (от n до 1). Осталось выяснить, как зависит от номера диагонали номер строки. Для нечетных диагоналей номер начальной строки должен быть равен (n-k+1). Поскольку в этом случае цикл возрастающий, то и номер строки должен возрастать. Для четных диагоналей этот номер должен убывать, а начальный номер, равен (2*m-k). Чтобы разнообразить задания можно связать их с задачами криптографии. Идея шифрования на матрице заключается в следующем: - берется фраза, которую необходимо зашифровать. Пусть это будет фраза – «привет студентам». - затем фраза последовательно (по буквам) записывается в квадратную матрицу по заданному маршруту обхода. Пусть это будет маршрут, приведенный на рисунке. Тогда после заполнения матрица будет выглядеть следующим образом: 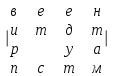 . .Если букв в исходной фразе не хватает для заполнения матрицы, то она заполняется случайными символами. - далее матрица разворачивается по строкам в одну строку. Тогда зашифрованная фраза будет выглядеть – «веенитдтр уапстм». Процесс расшифровки очевиден – из зашифрованной фразы составляется квадратная матрица, на которой по известному маршруту прочитывается исходная фраза. Варианты заданий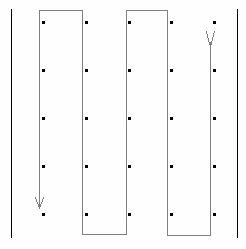 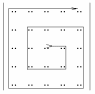 1) 2) 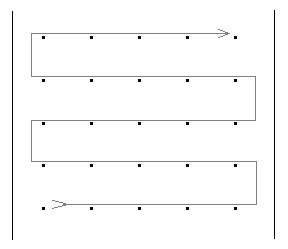 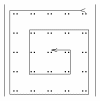 3) 4) 5 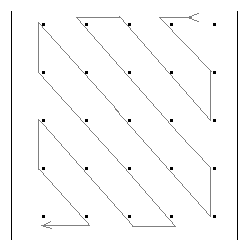 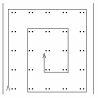 ) 6) ) 6)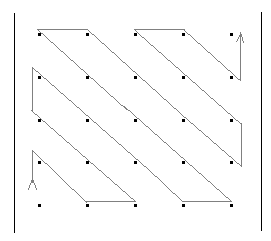 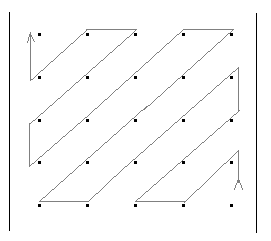 7) 8) 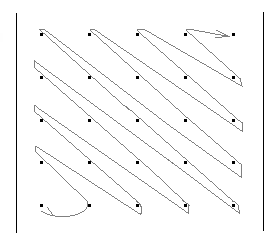 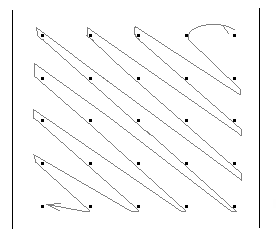 9) 10) 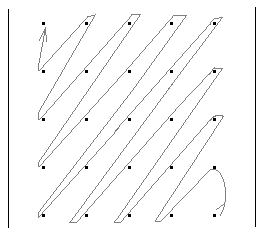 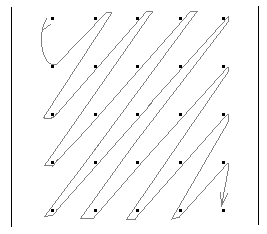 11) 12) 1   3) 14) 3) 14) |
