Математика. Форма обучения Очно-заочная Дружинин_№1 задания.. Задача Определить то значение параметра А, для которого функция будет непрерывной (если возможно). Сделать чертеж

• Название: Задача Определить то значение параметра А, для которого функция будет непрерывной (если возможно). Сделать чертеж
• Анкор: Математика
• Дата: 05.04.2023
• Размер: 0.61 Mb.
• Имя файла: Форма обучения Очно-заочная Дружинин_№1 задания..docx
• Тип: Задача; #1039467

Задача 1. Вычислить пределы данных функций

A)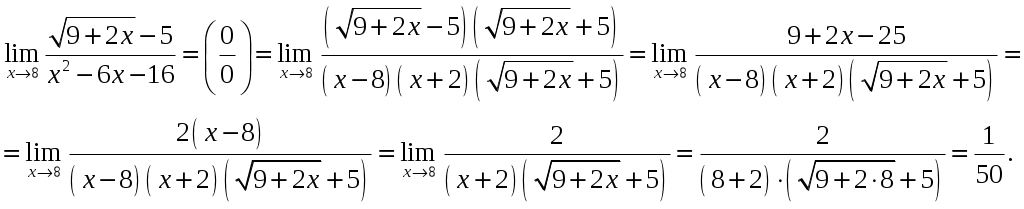



Б)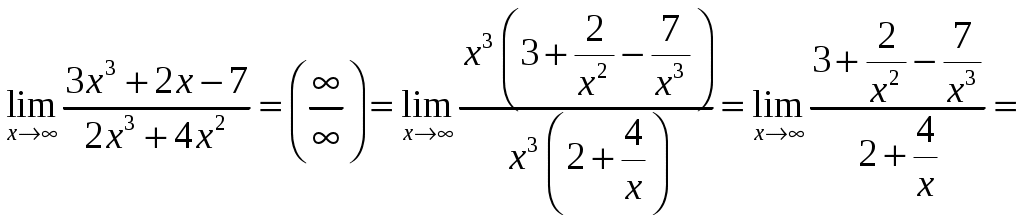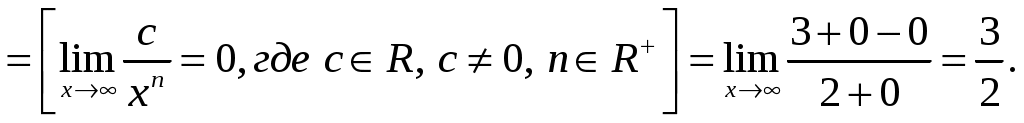





В)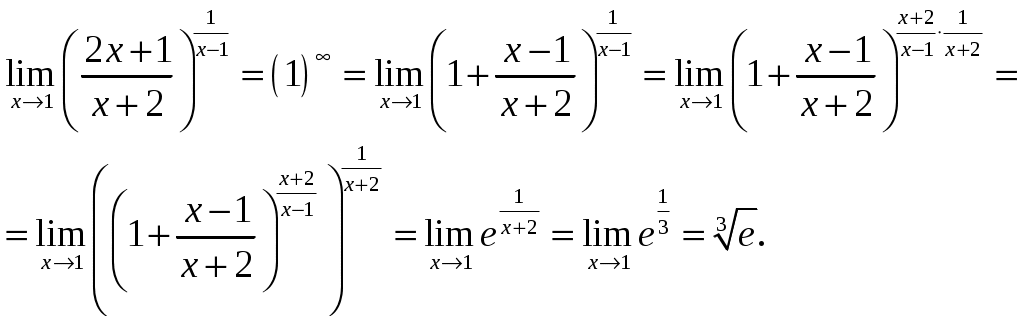



Г)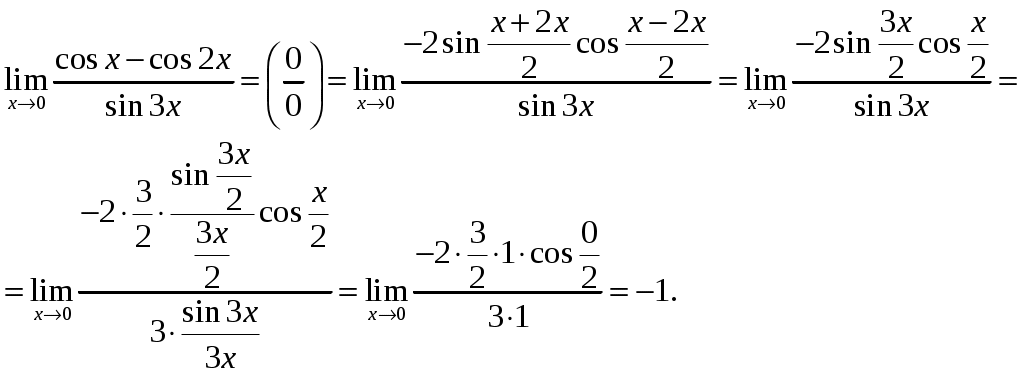



Задача 2. Определить то значение параметра А, для которого функция будет непрерывной (если возможно). Сделать чертеж.

Воспользуемся определением непрерывности функции: поскольку, и , то из равенства находим . Перепишем исходную функцию в виде

Воспользуемся определением непрерывности функции: поскольку   ,

 и   , то из равенства   находим   .

Перепишем исходную функцию в виде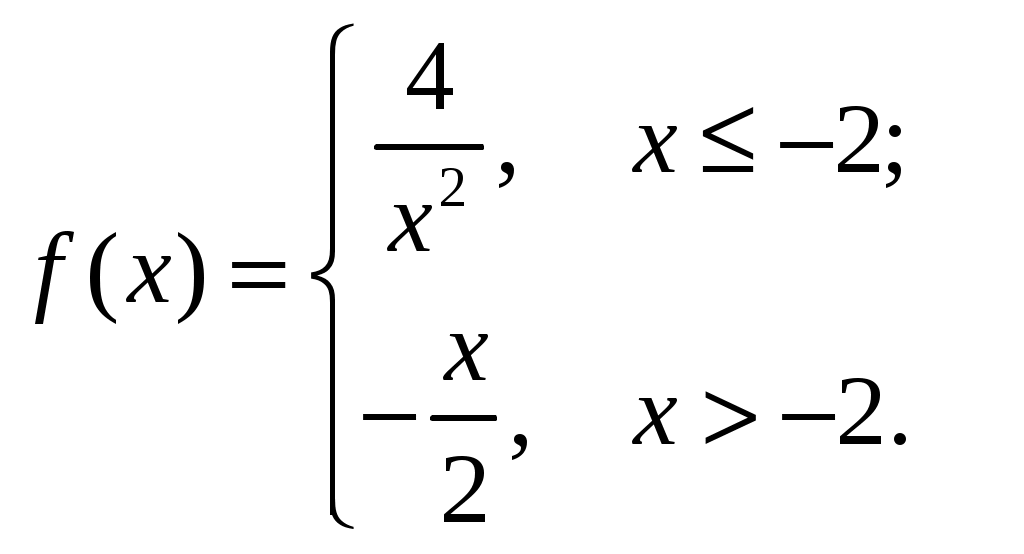



Сделаем чертеж.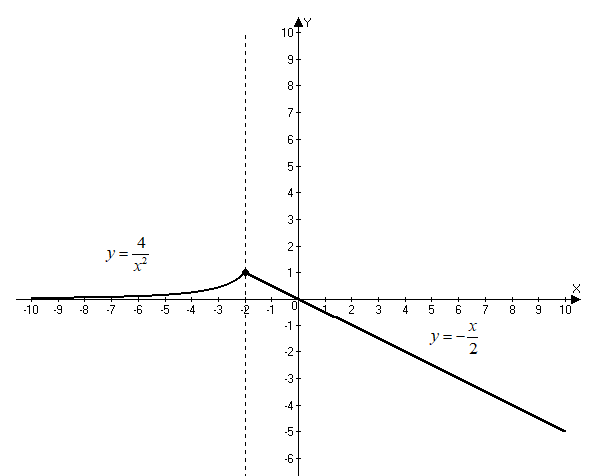



Задача 3. Исследовать функцию методами дифференциального исчисления и построить график.

Исследовать функцию методами дифференциального исчисления и построить график.



Решение.

Для полного исследования функции и построения ее графика применяется следующая примерная схема:

1. 
   найти область определения функции;
   
2. 
   исследовать функцию на непрерывность и определить характер точек разрыва;
   
3. 
   исследовать функцию на четность и нечетность, периодичность;
   
4. 
   найти точки пересечения графика функции с осями координат;
   
5. 
   исследовать функцию на монотонность и экстремум;
   
6. 
   найти интервалы выпуклости и вогнутости, точки перегиба;
   
7. 
   найти асимптоты графика функции;
   
8. 
   по полученным данным построить график функции.
   

Применим вышеуказанную схему для исследования данной функции.

1. 
    .
   
2. 
   Функция имеет точки разрыва   и   и непрерывна для всех   из области определения.
   
3. 
    .
   

Функция является нечетной. Функция не периодическая.

4. 
   С осью Ох:   .
   

Точка (0;0) – точка пересечения графика с осью Ох.

С осью Оу:   .

Точка (0;) – точка пересечения графика с осью Оу.

5. 
   Находим производную.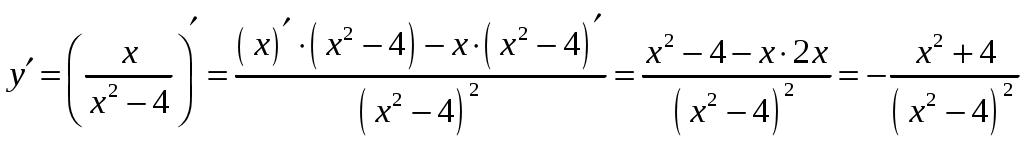
   

 при   и не существует при x=-2; x=2.

Исследуем знак производной функции на промежутках   , т.к. точки x=-2; x=2 точки разрыва

 – – –



 -2 2

Функция убывает – на всех 

6. 
   Находим вторую производную.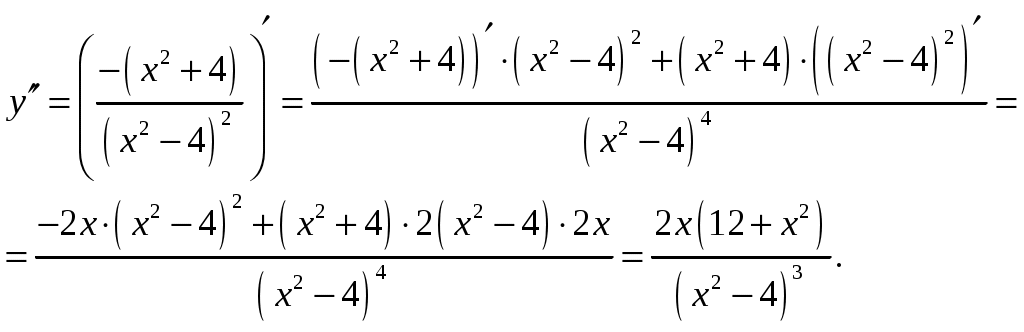
   

 при   и не существует при x=-2; x=2







– + – +

 -2 0 2
при     – кривая выпуклая,

при     – кривая вогнутая,

при     – кривая выпуклая,

при     – кривая вогнутая.

Точками перегиба являются точки разрыва и точка х=0.

 .

7. 
   Так как точки   и   - точки разрыва второго рода, то прямые   и   - вертикальные асимптоты.
   

Докажем это, исследуя поведение функции вблизи этих точек.





Найдем наклонные асимптоты 





Тогда   - горизонтальная асимптота

8. 
   
   По полученным данным строим график функции.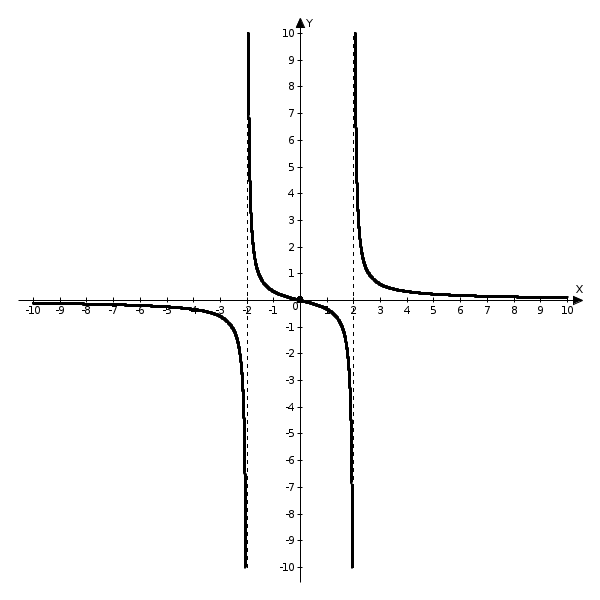
   

Задача 4. Найти все частные производные второго порядка, включая смешанную производную и дифференциал первого порядка от функции:

f = 8x2y – xcosy.

Решение.
Частные производные функции нескольких переменных определяются как производные этой функции по одному из них при условии, что остальные переменные считаются постоянными.
Сначала найдём частные производные первого порядка:





Теперь находим производные второго порядка по переменным   и   :

 

Находим смешанные производные:





Полный дифференциал функции находим по формуле:



Получаем:



Задача 5. Исследовать на экстремум функцию f = x2 + 4xy – y2+2x + 4y + 7.

Решение.

Для нахождения точек экстремума, применим необходимое условие локального экстремума дифференцируемой функции:

 

 ;

 .

Получаем:



Точки   – точка экстремума.

Для проверки наличия и характера экстремума функции в точке требуется определить знак определителя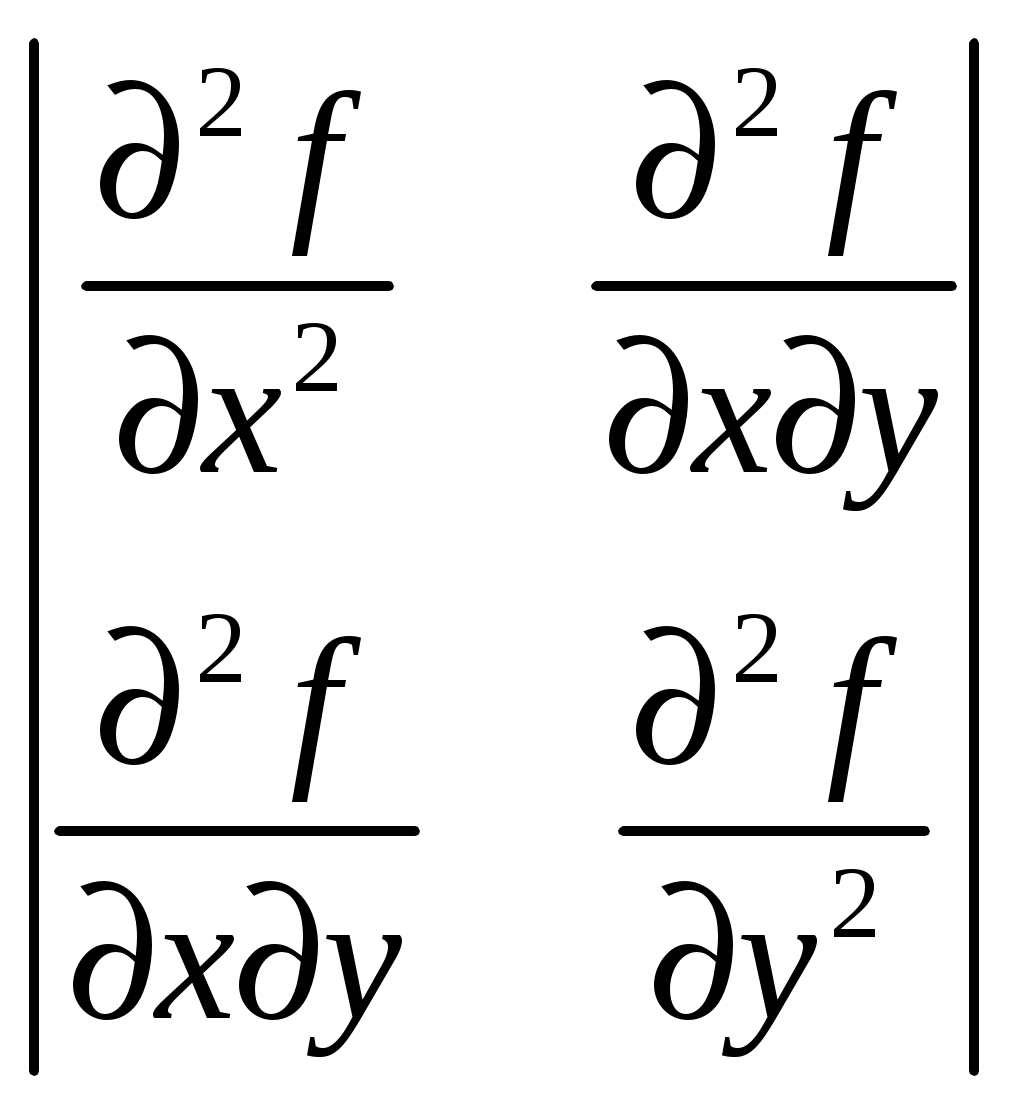



Вычислим частные производные второго порядка:

   

Тогда   .

В точке   :   – экстремума нет.

Ответ: экстремума нет.