Задача 1. Задача расчет статически неопределимой рамы методом сил порядок выполнения работы
 Скачать 1.34 Mb. Скачать 1.34 Mb.
|
|
ЗАДАЧА 1.РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ МЕТОДОМ СИЛ ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Установить степень свободы статической неопределимости рамы. 2. Выбрать несколько вариантов основной системы и обосновать рациональность принятой к расчету основной системы. 3. Написать канонические уравнения в общем виде. 4. Построить эпюры изгибающих моментов от единичных сил и заданной нагрузки. 5. Вычислить коэффициенты при неизвестных и свободные члены канонических уравнений. 6. Выполнить универсальную проверку коэффициентов, при неизвестных и свободных членах канонических уравнений. 7. Найти неизвестные усилия, решив систему канонических уравнений. 8. Построить окончательную эпюру изгибающих моментов в заданной системе. 9. Выполнить деформационную проверку. 10. Построить эпюры поперечных и продольных сил. Эпюру поперечных сил построить по окончательной эпюре изгибающих моментов, на основе теоремы Журавского, а эпюру продольных сил построить по эпюре поперечных сил, рассматривая равновесие вырезанных узлов. 11. Выполнить статическую проверку всей рамы в целом, ее отдельных узлов и сквозных сечений. Таблица 1
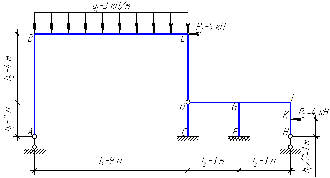 Рисунок 1 Решение. 1. Число степеней свободы вычисляем по следующей формуле: 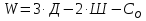 где 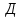 – число дисков в системе (без учета диска «земля»), ABDE, CD, DFGHKL, – число дисков в системе (без учета диска «земля»), ABDE, CD, DFGHKL, 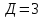 ; ;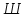 – число простых шарниров, соединяющих диски, – число простых шарниров, соединяющих диски, 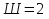 ; ;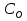 – число опорных стержней, соединяющих систему с диском «земля» (заделки C и F каждая эквивалентна трем опорным стержням, шарнирно-подвижные опоры A и H каждая эквивалентна одному опорному стрежню), – число опорных стержней, соединяющих систему с диском «земля» (заделки C и F каждая эквивалентна трем опорным стержням, шарнирно-подвижные опоры A и H каждая эквивалентна одному опорному стрежню), 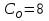 . .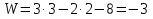 Степень статической неопределимости  Рассматриваемая рама трижды статически неопределима. 2. Для заданной рамы возможно несколько основных систем (рисунок 2). 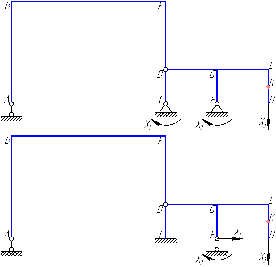 Рисунок 2 Критериями выбора основной системы являются простота построения эпюр в грузовом и единичных состояниях и минимум участков, на которые распространяются эпюры. Выбранная основная система для рассматриваемой рамы представлена на рисунке 3. 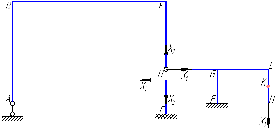 Рисунок 3 3. Система канонических уравнений для заданной рамы будет иметь следующий вид: 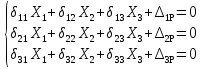 4. Построим единичную эпюру изгибающих моментов  в основной системе от действия силы в основной системе от действия силы  (рисунок 4). (рисунок 4).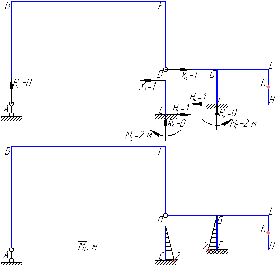 Рисунок 4 Определим реакции опор: 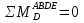 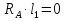 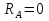 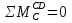 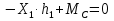 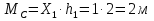 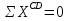 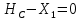 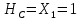 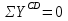 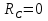 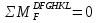 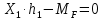 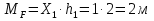  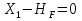 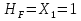 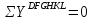  Построим единичную эпюру изгибающих моментов 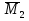 в основной системе от действия силы в основной системе от действия силы 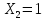 (рисунок 5). (рисунок 5).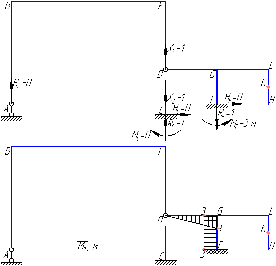 Рисунок 5 Определим реакции опор: 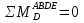 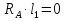 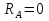 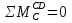 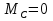 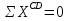 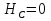 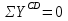 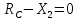 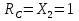 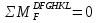 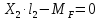 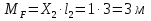  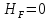 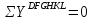 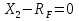 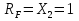 Построим единичную эпюру изгибающих моментов  в основной системе от действия силы в основной системе от действия силы 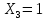 (рисунок 6). (рисунок 6).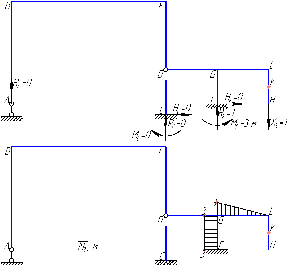 Рисунок 6 Определим реакции опор: 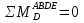 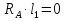 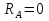 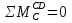 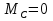 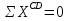 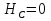 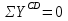 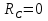 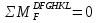 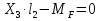 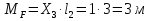  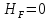 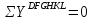 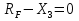 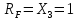 Построим грузовую эпюру изгибающих моментов 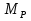 в основной системе от внешней нагрузки (рисунок 7). в основной системе от внешней нагрузки (рисунок 7).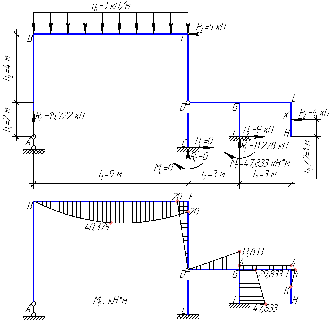 Рисунок 7 Определим реакции опор: 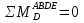 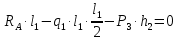 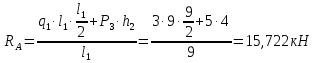   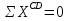 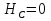 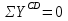 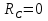 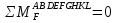 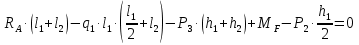 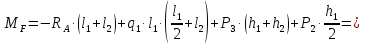 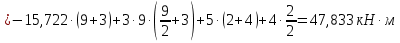 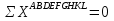 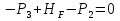 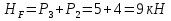 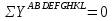 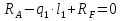 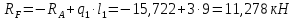 5. Единичное перемещение  и грузовое перемещение и грузовое перемещение  вычисляются по формуле Мора: вычисляются по формуле Мора: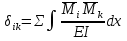 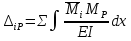 Вычисление интегралов Мора производится перемножением эпюр по правилу Верещагина. Определим единичные и грузовые перемещения: 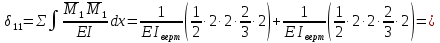 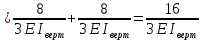 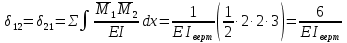 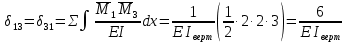 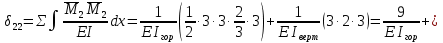 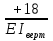 По условию: 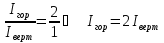 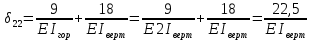 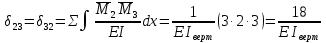 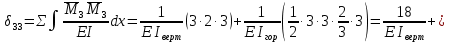 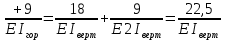 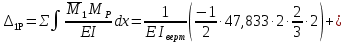 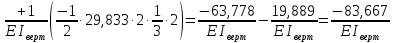 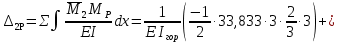 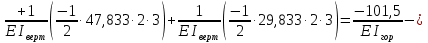 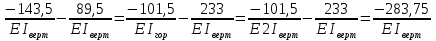 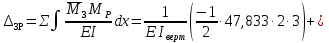 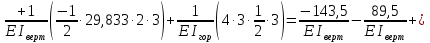 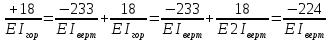 6. Проверка коэффициентов канонических уравнений. Построим суммарную эпюру изгибающих моментов 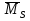 в основной системе от действия сил в основной системе от действия сил 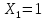 , , 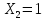 и и 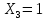 (рисунок 8). (рисунок 8). Рисунок 8 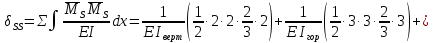 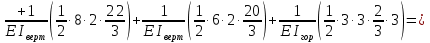 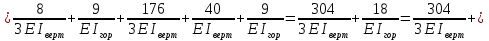 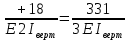 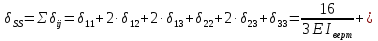  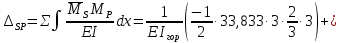 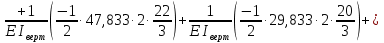 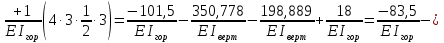 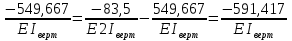 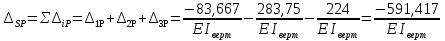 Проверка показала правильность определения коэффициентов. 7. Решение системы уравнений. 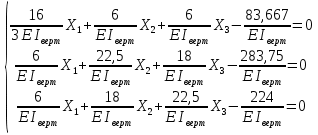 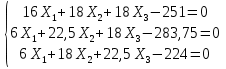 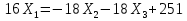 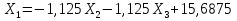 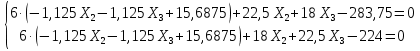 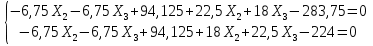 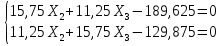 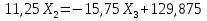 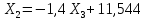 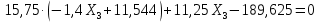 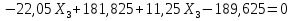 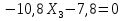 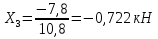 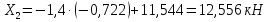 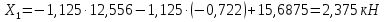 Проверка: 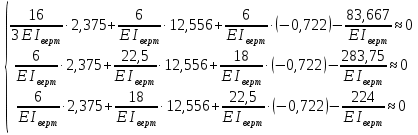 8. После определения значений неизвестных строим для основной системы эпюры изгибающих моментов от каждого из найденных усилий.  Рисунок 9 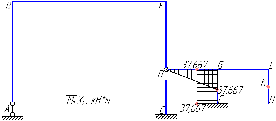 Рисунок 10 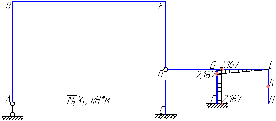 Рисунок 11 Просуммировав по характерным точкам на протяжении всей рассчитываемой рамы ординаты эпюр от действия всех сил  с ординатами грузовой эпюры, получим окончательную эпюру изгибающих моментов в заданной статически неопределимой системе (рисунок 12): с ординатами грузовой эпюры, получим окончательную эпюру изгибающих моментов в заданной статически неопределимой системе (рисунок 12):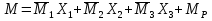 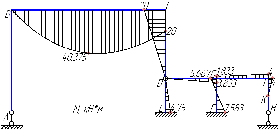 Рисунок 12 9. Деформационная проверка. Для этого необходимо перемножить суммарную единичную и окончательную эпюры изгибающих моментов: 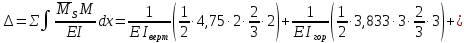 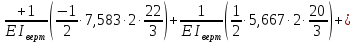 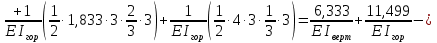 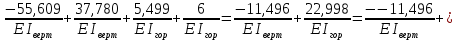 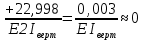 10. Эпюру поперечных сил  на каждом участке строим по эпюре изгибающих моментов по формулам: на каждом участке строим по эпюре изгибающих моментов по формулам: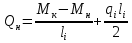 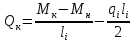 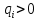 , если равномерно распределенная нагрузка направлена вниз; изгибающие моменты в начале участка , если равномерно распределенная нагрузка направлена вниз; изгибающие моменты в начале участка 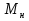 и в конце участка и в конце участка 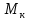 положительны, если растягивают нижние волокна. Для вертикальных стержней условно принимаем правые волокна за нижние. положительны, если растягивают нижние волокна. Для вертикальных стержней условно принимаем правые волокна за нижние.Участок AB. 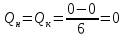 Участок BE. 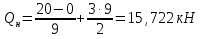 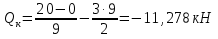 Участок CD. 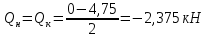 Участок DE. 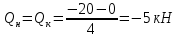 Участок DG. 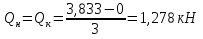 Участок FG. 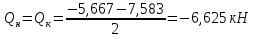 Участок GL. 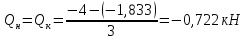 Участок HK. 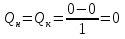 Участок KL. 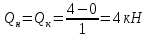 По данным проведенного расчета строим эпюру поперечных сил  (рисунок 13). (рисунок 13).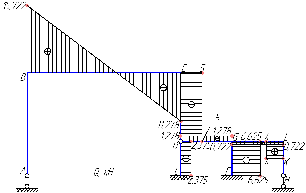 Рисунок 13 Для построения эпюры 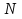 используем метод вырезания узлов. используем метод вырезания узлов.Узел B. 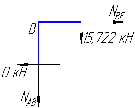 Рисунок 14 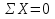 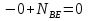 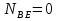 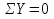 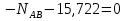 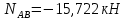 Узел E. 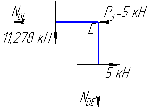 Рисунок 15  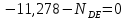 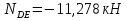 Узел L. 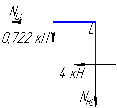 Рисунок 16 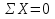 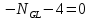 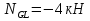 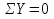 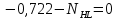 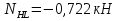 Узел G. 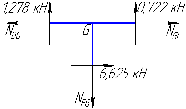 Рисунок 17 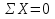 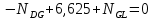 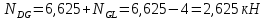 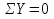 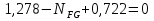 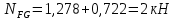 Узел D. 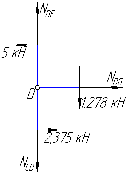 Рисунок 18 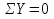 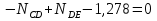 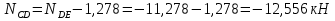 По данным проведенного расчета построим эпюру продольных сил 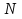 (рисунок 19). (рисунок 19).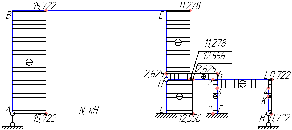 Рисунок 19 11. Для построенной окончательной эпюры изгибающих моментов убедимся в равновесии узлов. Узел E. 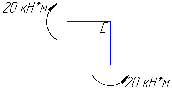 Рисунок 20 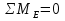 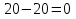 Узел G.  Рисунок 21 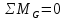 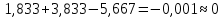 Узел L.  Рисунок 22   Статическая проверка состоит в проверке равновесия заданной рамы от действия внешней нагрузки и реакций опор, определенных по эпюрам поперечных и продольных сил (рисунок 23). 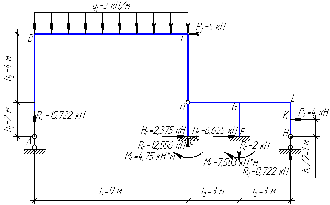 Рисунок 23 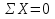 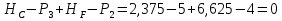 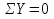 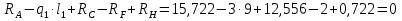 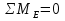 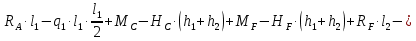 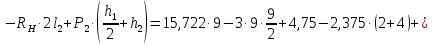 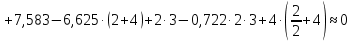 Выполнение деформационной и статической проверок подтверждает правильность построения эпюр 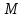 , , 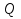 , , 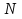 . . |

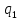 ,
,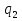 ,
,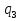 ,
,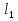 ,
,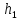 ,
,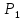 ,
,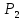 ,
, ,
,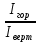
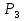 ,
,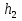 ,
,