Математика-3. Задача Решите уравнение Решение Применим метод алгебраических дополнений. Получим нули в столбце 1
 Скачать 455 Kb. Скачать 455 Kb.
|
|
Контрольная работа по математике Вариант 3 Задача 1. Решите уравнение: 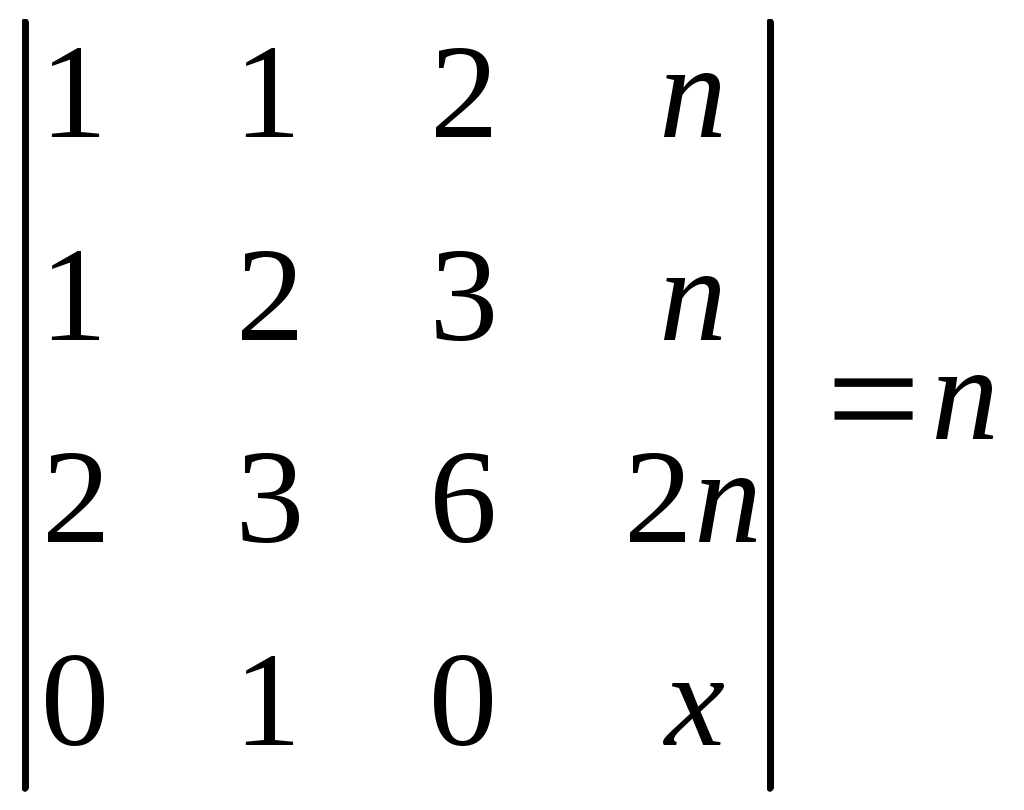 Решение Применим метод алгебраических дополнений. Получим нули в столбце 1. Из строки 2 вычтем почленно строку 1:
Затем из строки 3 вычтем строку 1, предварительно умножив строку 1 на 2.
Строку 4 перепишем, так как в ней есть 0. В результате получим определитель, равный исходному: 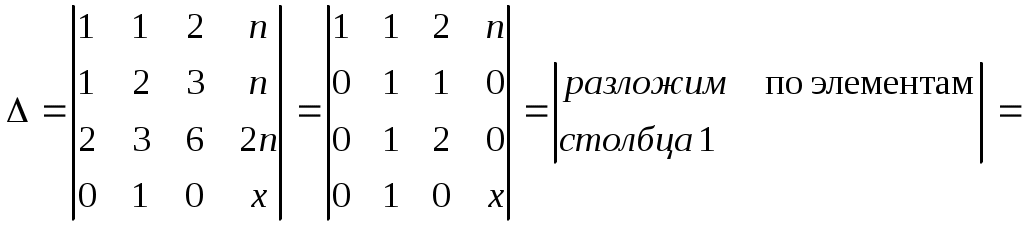 = Вычислив алгебраическое дополнение А11: 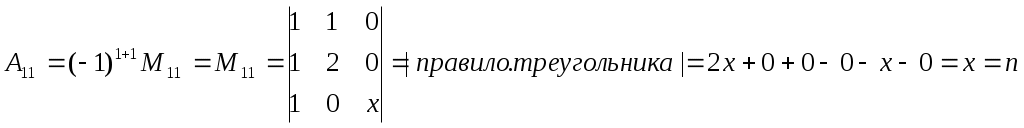 =3 =3Ответ: х=3 Задача 2. Даны матрицы 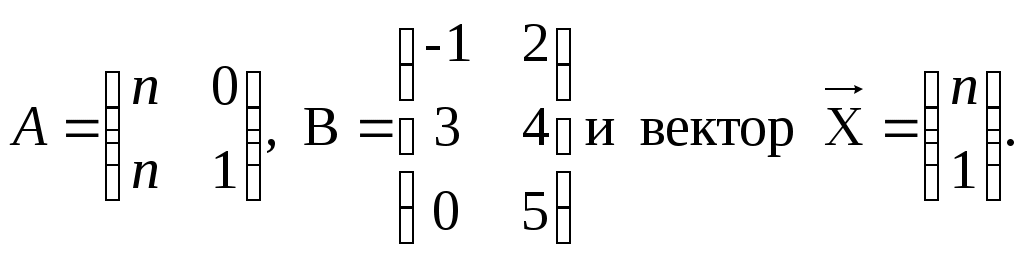 Найдите: ВА, АХ, ХА, А-1, АT , rangА, D=n(АT)Т – АЕ. Решение 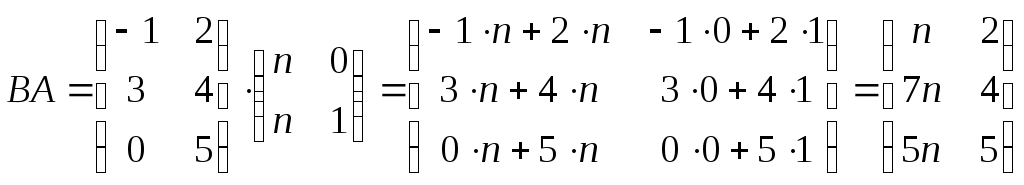 = = 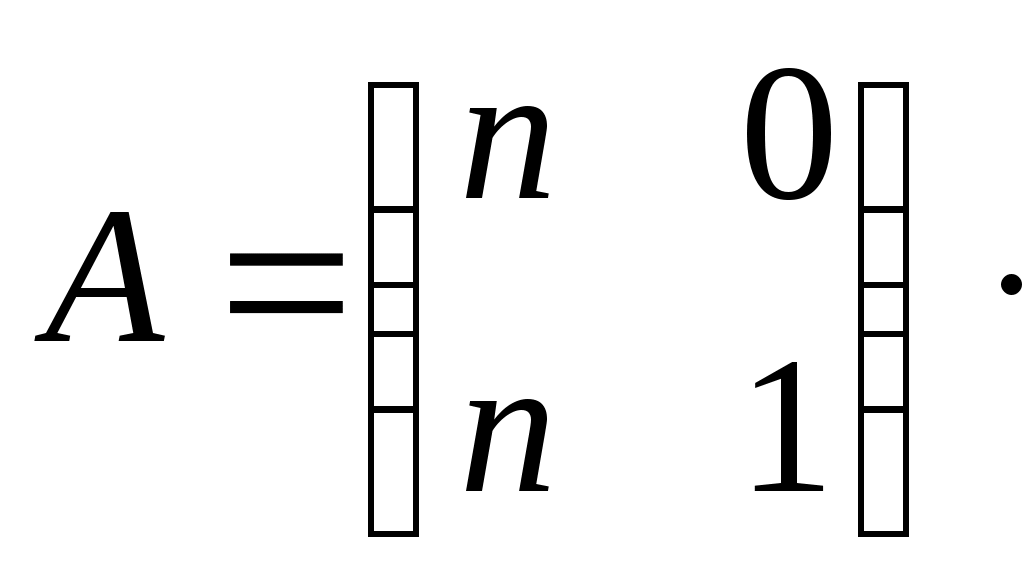 Произведение ХА не определено, так число столбцов в Х неравно числу строк А. Обратная матрица. Если 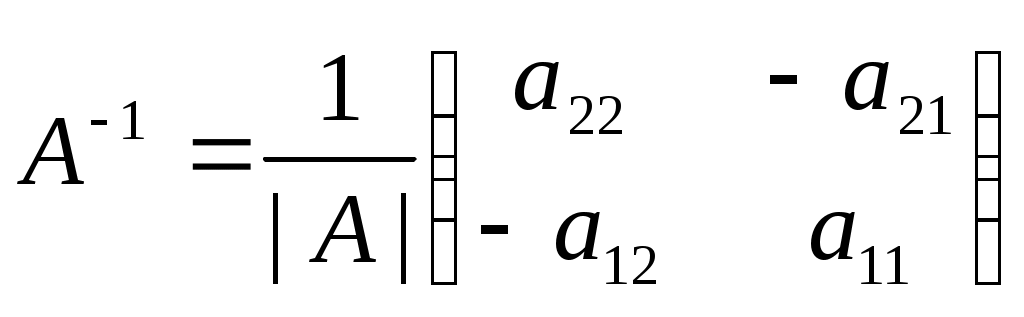 , то , то 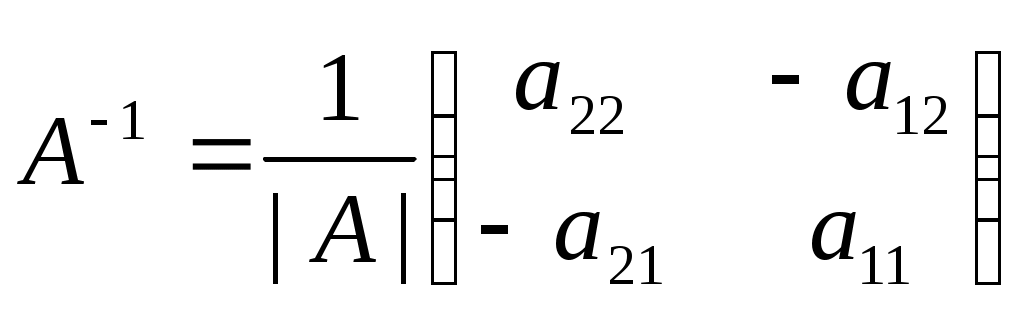 Определитель матрицы Тогда Транспонирование матрицы: Ранг А равен 2, так как Применим свойства матриц: D=n(АT)Т – АЕ= nА – А=(n-1)А = =(n-1) Задача 3. Исследуйте систему линейных уравнений с помощью определителей, решите методами Крамера, матричным, Гаусса. 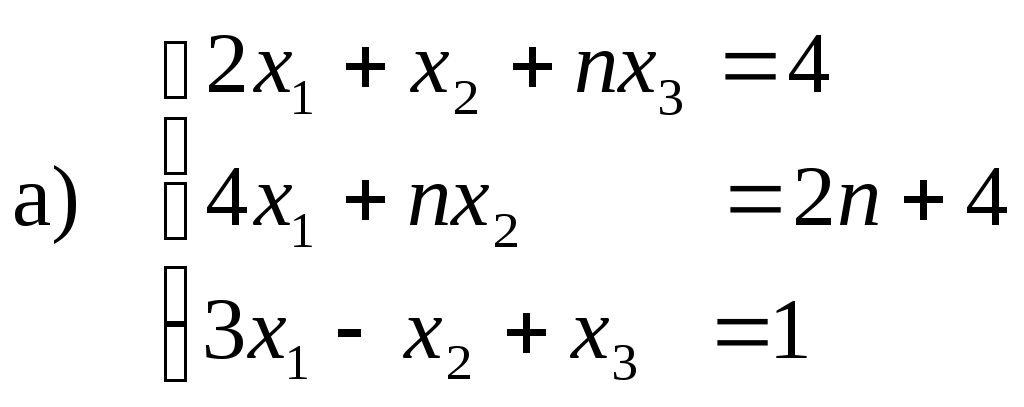 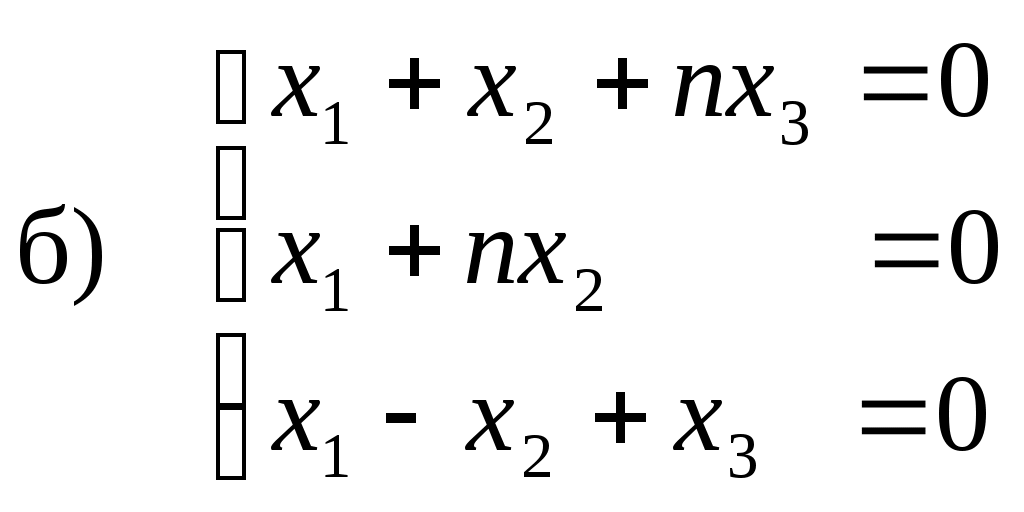 Решение Найдем определитель системы: 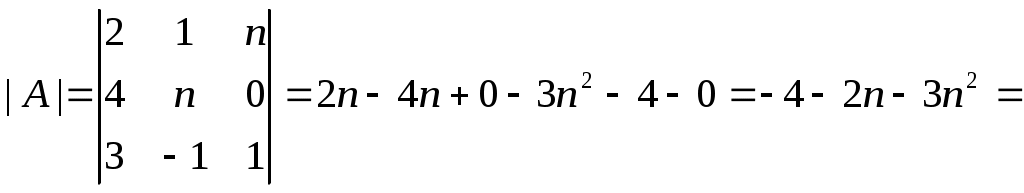 -4-6-27= -370 -4-6-27= -370Система имеет единственное решение. 1) Метод Крамера. где Δ – определитель системы, Δхj - вспомогательные определители, каждый из которых получается из определителя Δ заменой столбца j столбцом свободных членов вi. Найдем вспомогательные определители: 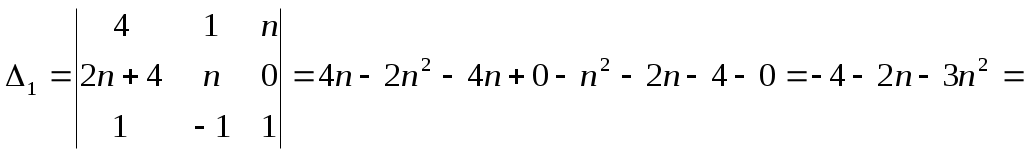 -37 -37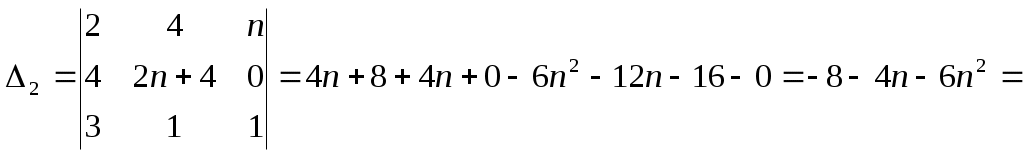 -74 -74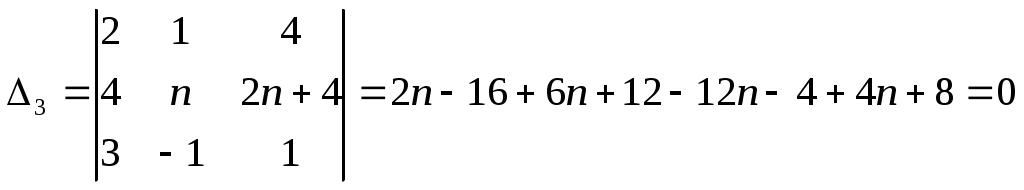 Найдем значения неизвестных: 2) Матричный метод: X= А-1В. Матрицы системы: 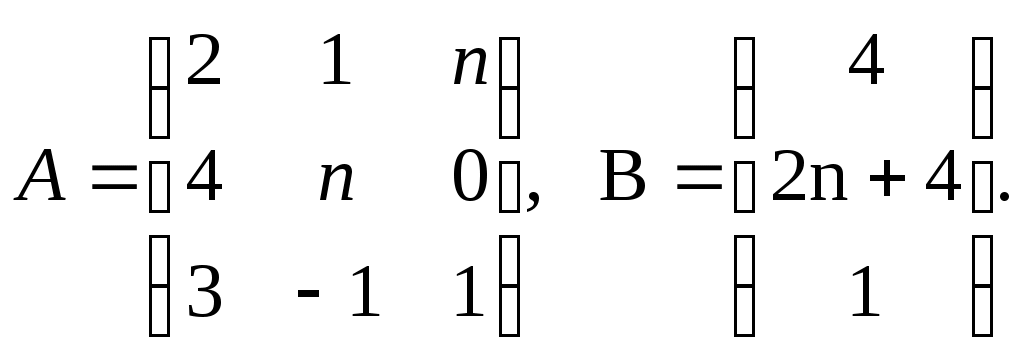 Найдем обратную матрицу: 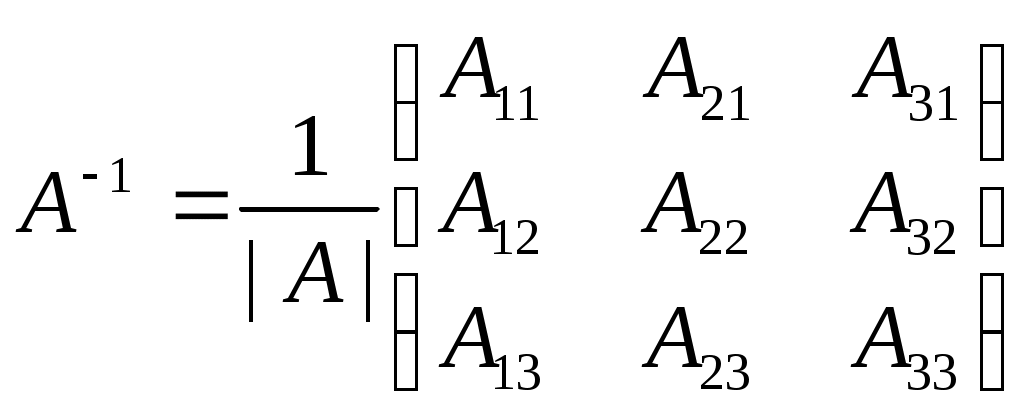 Определитель системы: 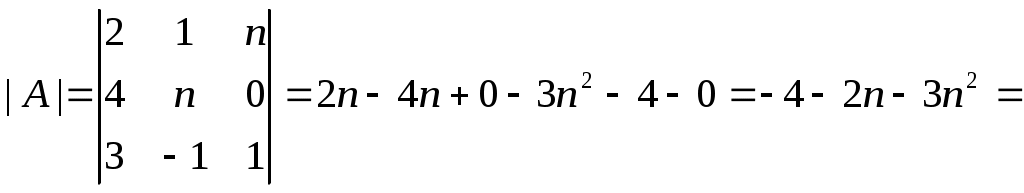 -37 -37Найдем алгебраические дополнения: Аij=(-1)i+jMij А11=(-1)1+1М11=+М11= А21=(-1)2+1М21=-М21= - Аналогично находим остальные дополнения. Получим: 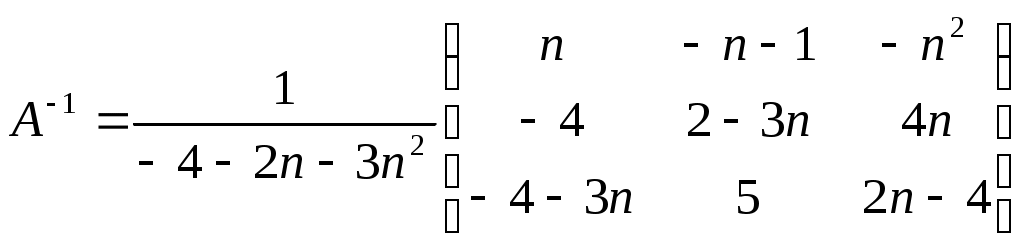 Найдем матрицу неизвестных: 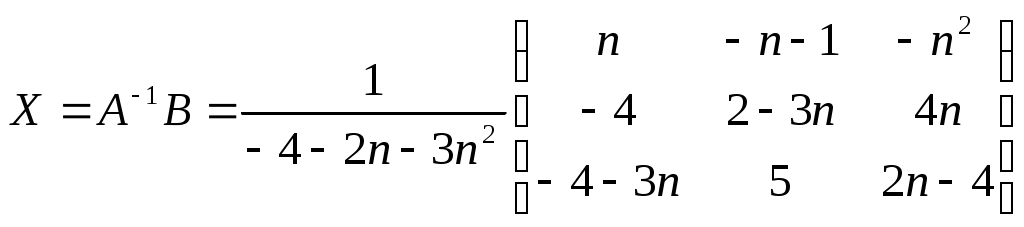 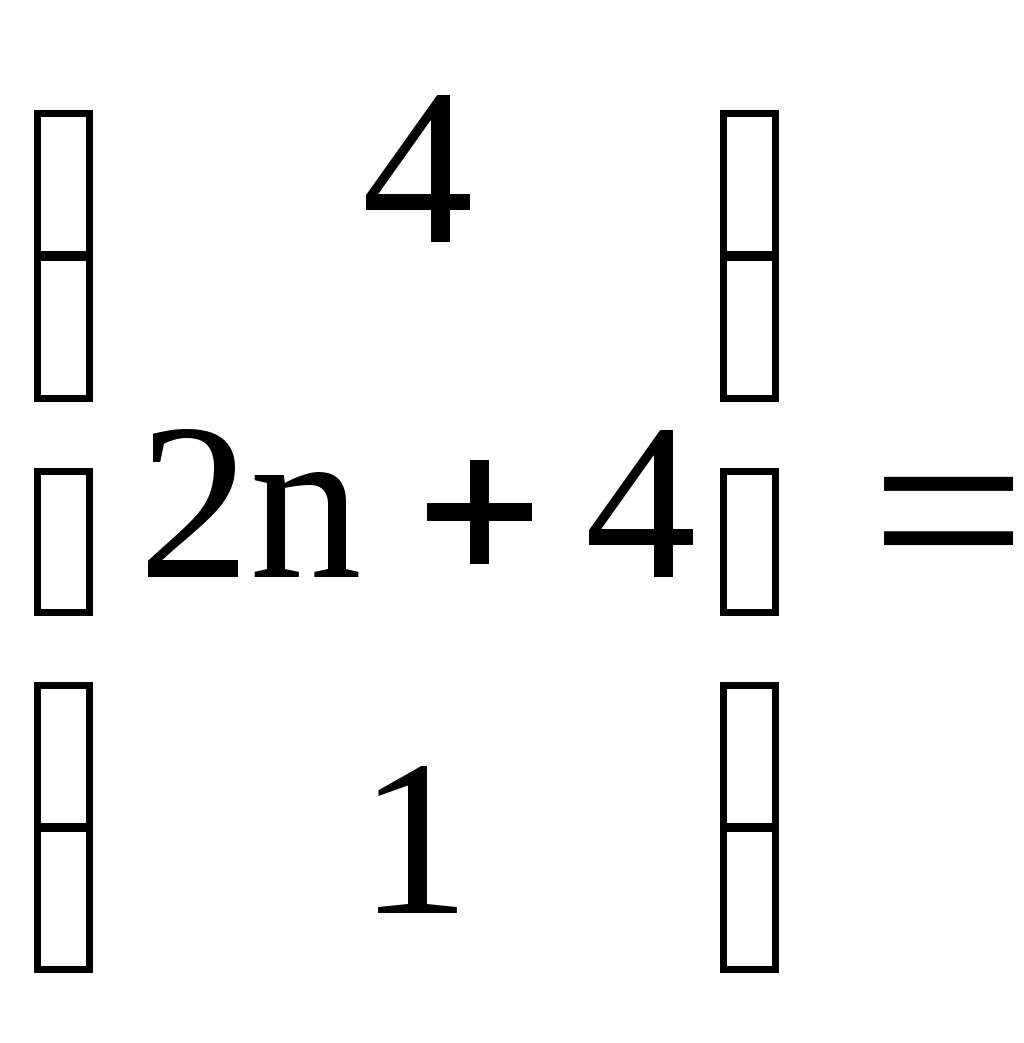 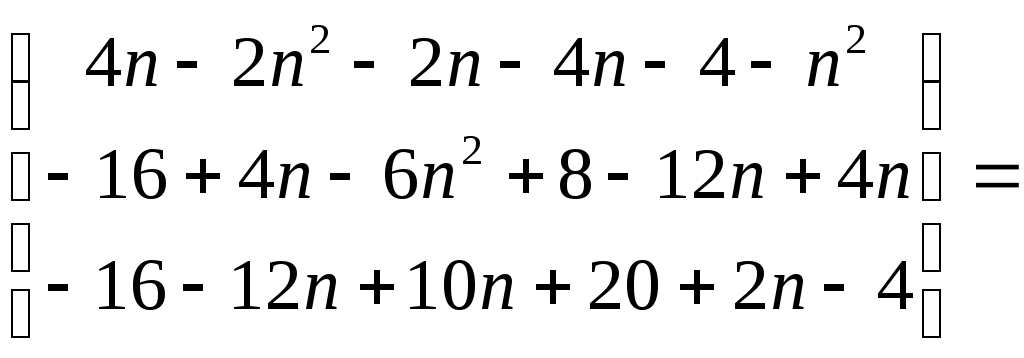 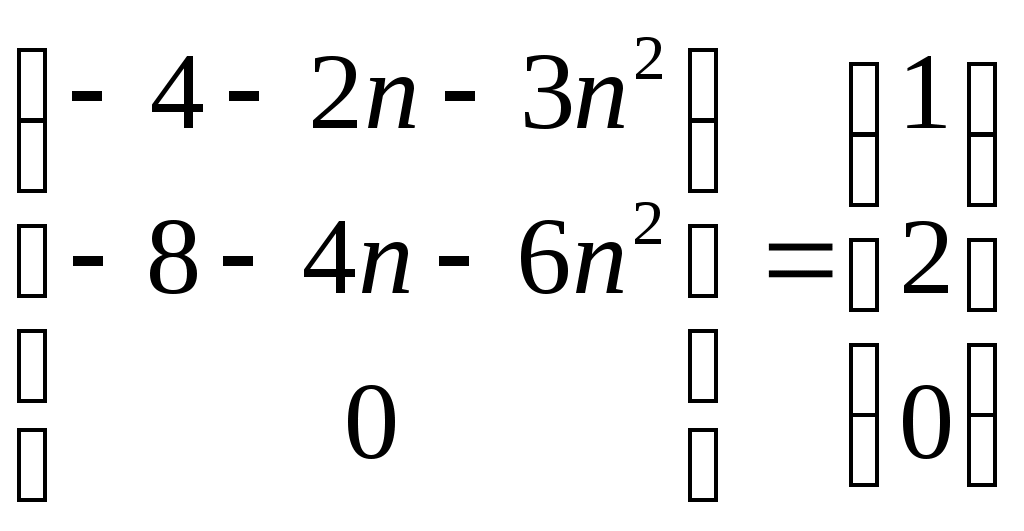 3) Метод Гаусса 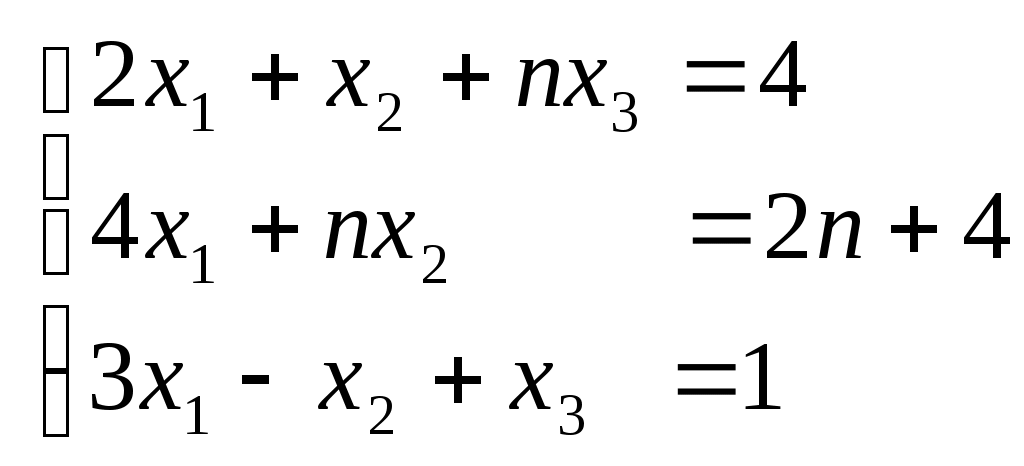 Приведем систему с помощью элементарных преобразований к равносильной системе ступенчатого вида. Исключим неизвестную x1 Первое уравнение поделим на 2, получим: Из второго уравнения вычтем почленно новое первое уравнение, умноженное на 4: (n-2)x2-2nx3=2n-4 Из третьего уравнения вычтем почленно новое первое уравнение, умноженное на 3: 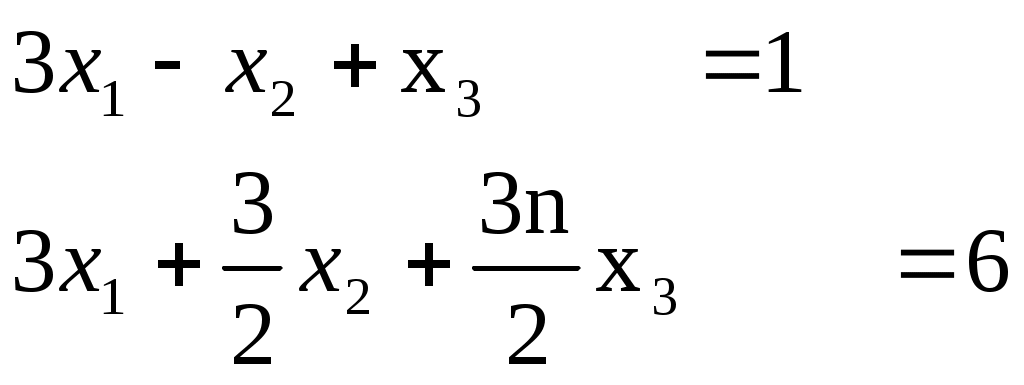 В результате получим равносильную систему: 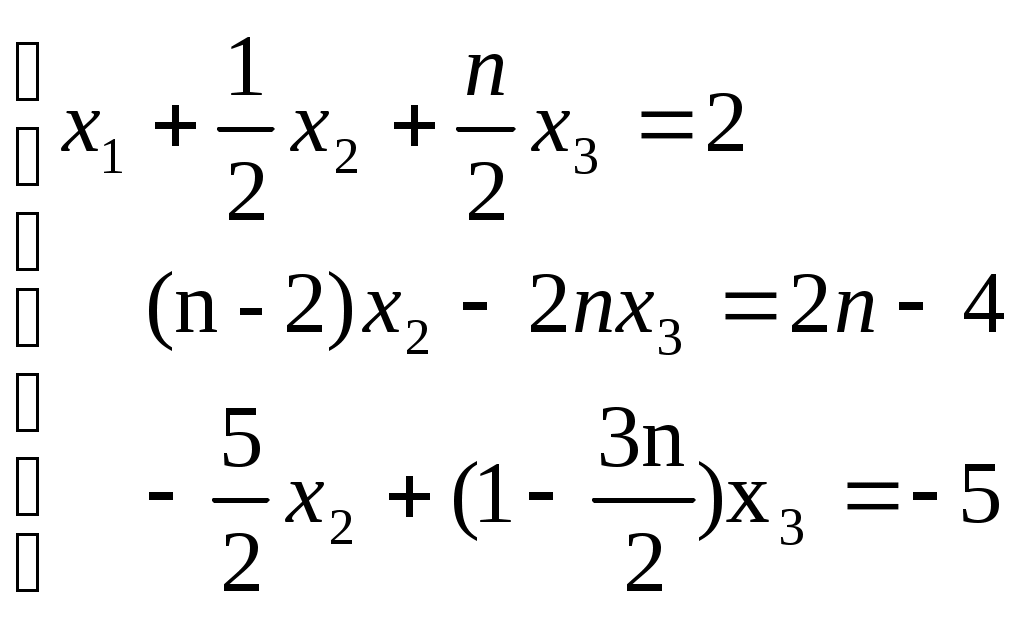 Исключим неизвестную x2 Поменяем местами второе и третье уравнения: 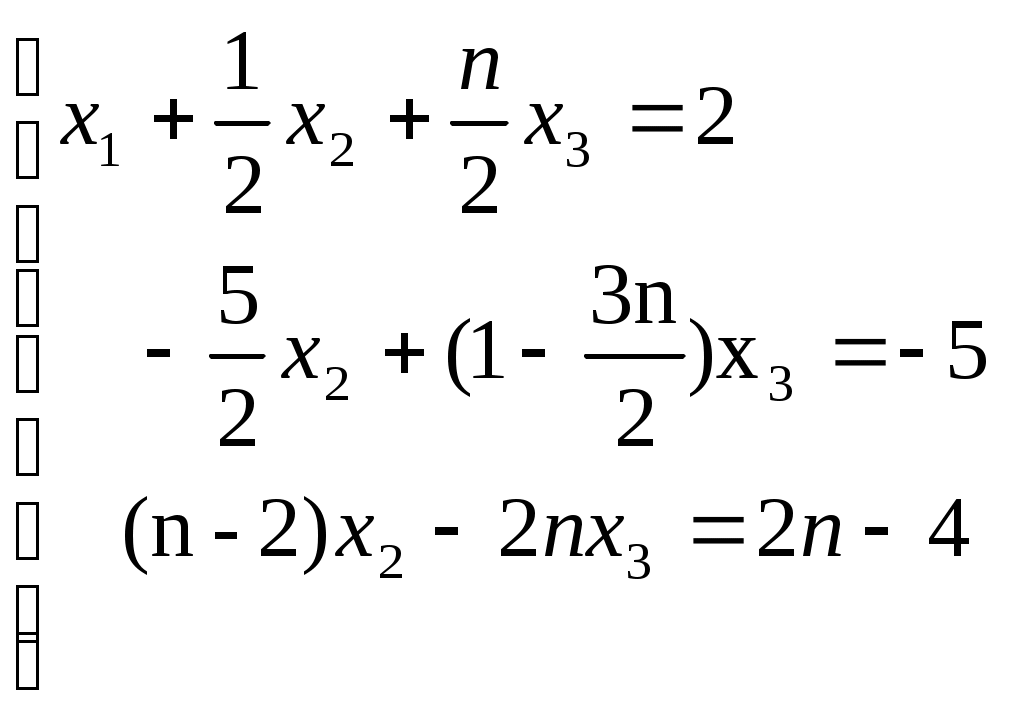 Поделим второе уравнение на (-5/2): Из третьего уравнения вычтем второе, умноженное на (n-2): 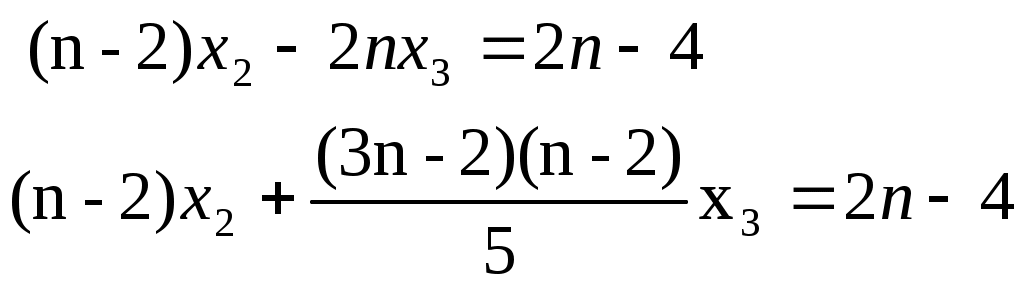 В результате получим равносильную систему: 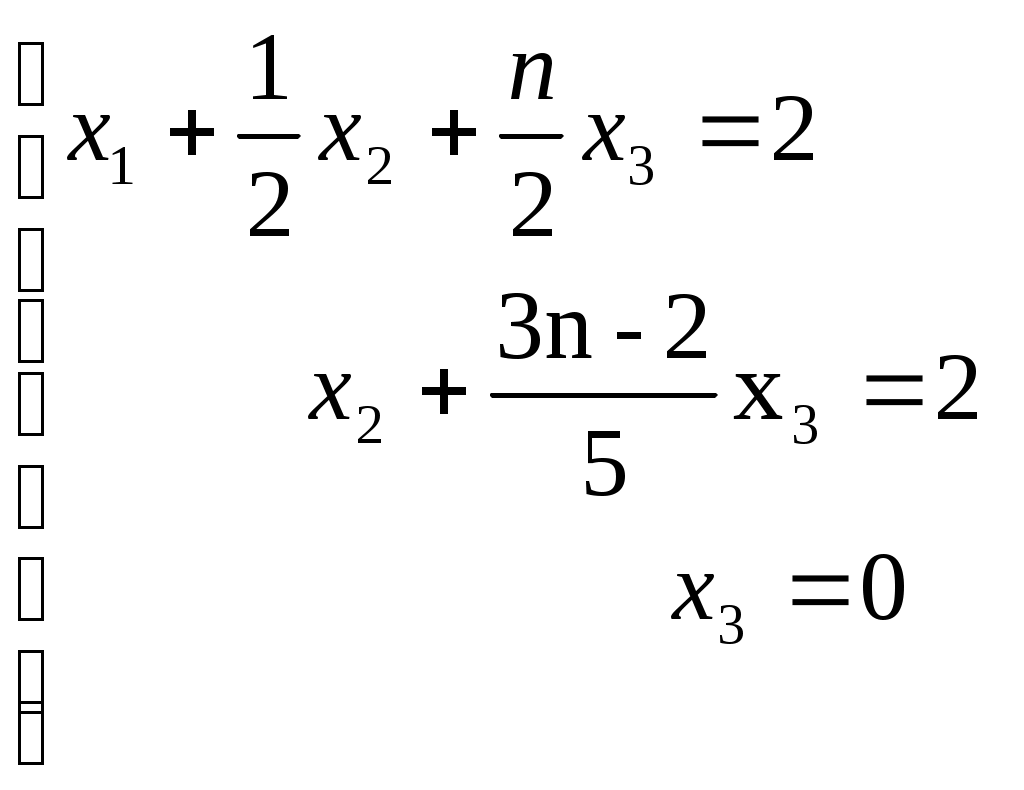 Из второго уравнения при x3=0 получим x2=2. Из первого уравнения: Проверка: 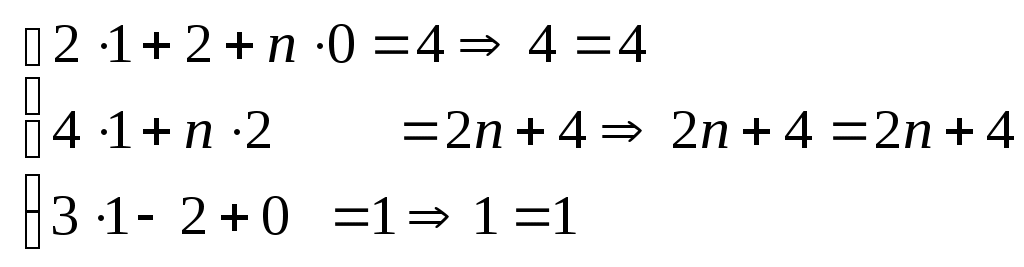 Система решена правильно Ответ: х1=1, х2=2, х3=0. Задача 4. Постройте векторы а) площадь треугольника, построенного на б) объем пирамиды, построенной на векторах Решение Построим векторы. 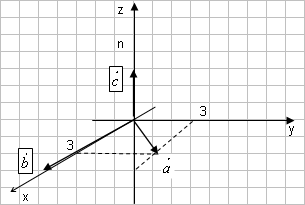 а) площадь треугольника, построенного на Используем геометрический векторного произведения: 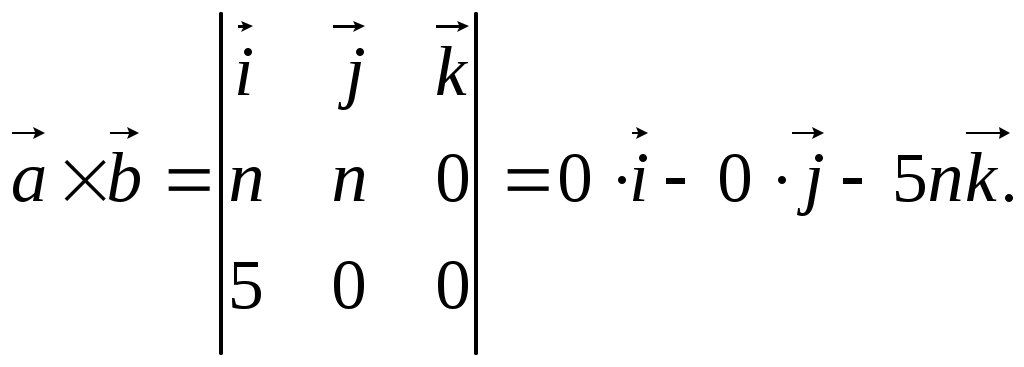 Модуль вектора Тогда б) Объем пирамиды Используем геометрический смысл смешанного произведения: 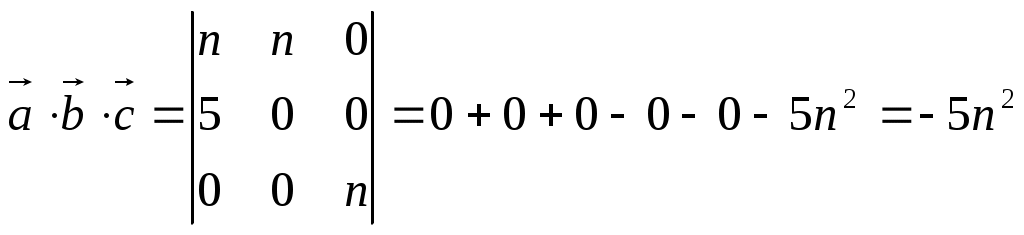 . . Тогда Задача 5. Даны координаты вершин треугольника АВС: А(n-10,2), В(1,n-10), С(0,5) Сделайте чертеж. Найдите: 1) длину и уравнение медианы АН; 2) длину и уравнение высоты AD. Решение Сделаем чертеж. 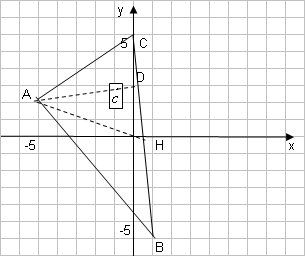 1) Длина и уравнение медианы АН Сначала найдем координаты точки М как середины отрезка ВС: Подставляя координаты точек А и М в уравнение: Получим: Длина АМ: 2) Длина и уравнение высоты AD Прямые АD и ВС перпендикулярны, поэтому их угловые коэффициенты Уравнение ВС: Тогда: у-уо=k(х-хо) Задача 6. Даны координаты вершин пирамиды М1М2М3М4: М1(2,0,0), М2(0,-4,2), М3(0,n,0), М4(0,0,4). Сделайте чертеж. Найдите: 1) уравнение и длину ребра М1М2; 2) угол между рёбрами М1М2 и М1М4; 3) уравнение грани М1М2М3; 4) площадь грани М1М2М3; 5) объём пирамиды. Решение Сделаем чертеж. 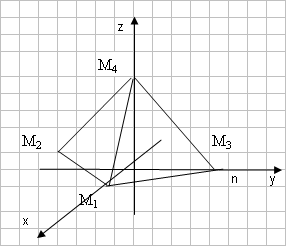 1) уравнение и длина ребра М1М2; Уравнения ребра М1М2 найдем как уравнения прямой, проходящей через две точки. Подставляя координаты точек в уравнения получим: Длина ребра М1М2 равна расстоянию между точками М1и М2 или длине вектора: 2) угол между рёбрами М1М2 и М1М4 Определим угол между сторонами М1М2 и М1М4 как угол между соответствующими векторами. Найдем координаты векторов: 3) уравнение грани М1М2М3 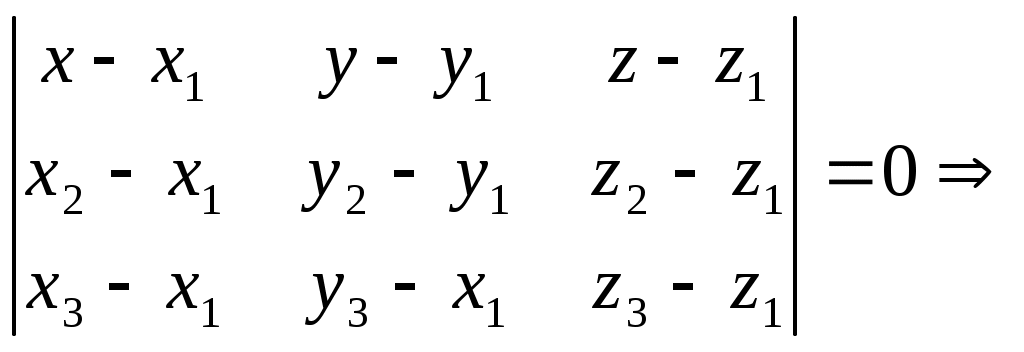 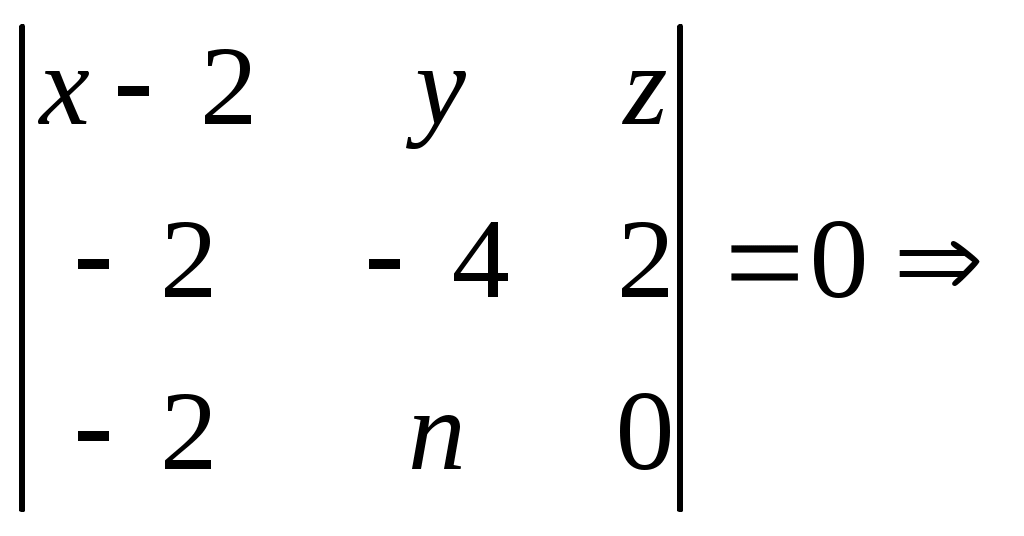 0-2nz-4y-8z-0-2n(x-2)=0 -2nx-4y-(8+2n)z+4n=0 nx+2y+(4+n)z-2n=0 Нормальный вектор плоскости 4) площадь грани М1М2М3 5) объём пирамиды. Используем геометрический смысл смешанного произведения: Координаты векторов: Найдем смешанное произведение 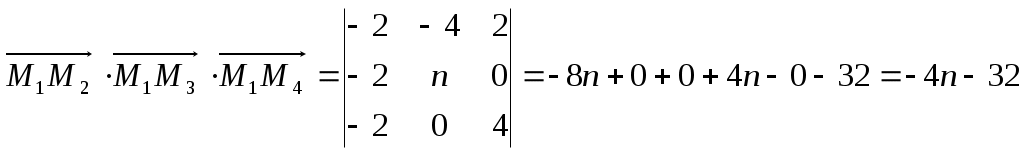 . . Тогда Задача 7. Найдите пределы: а) в) Решение а) при k=0 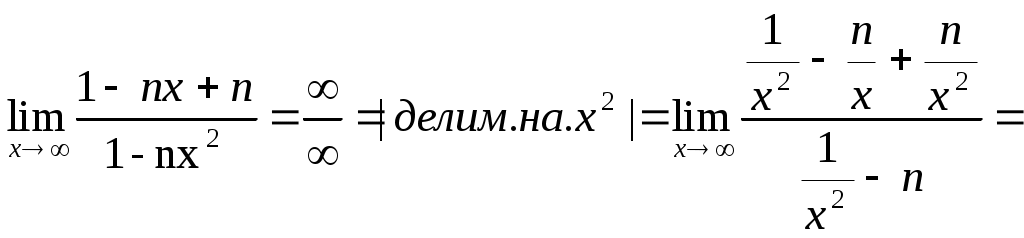  при k=2 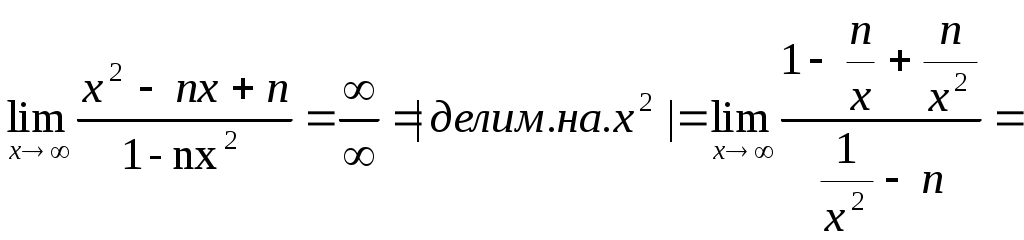 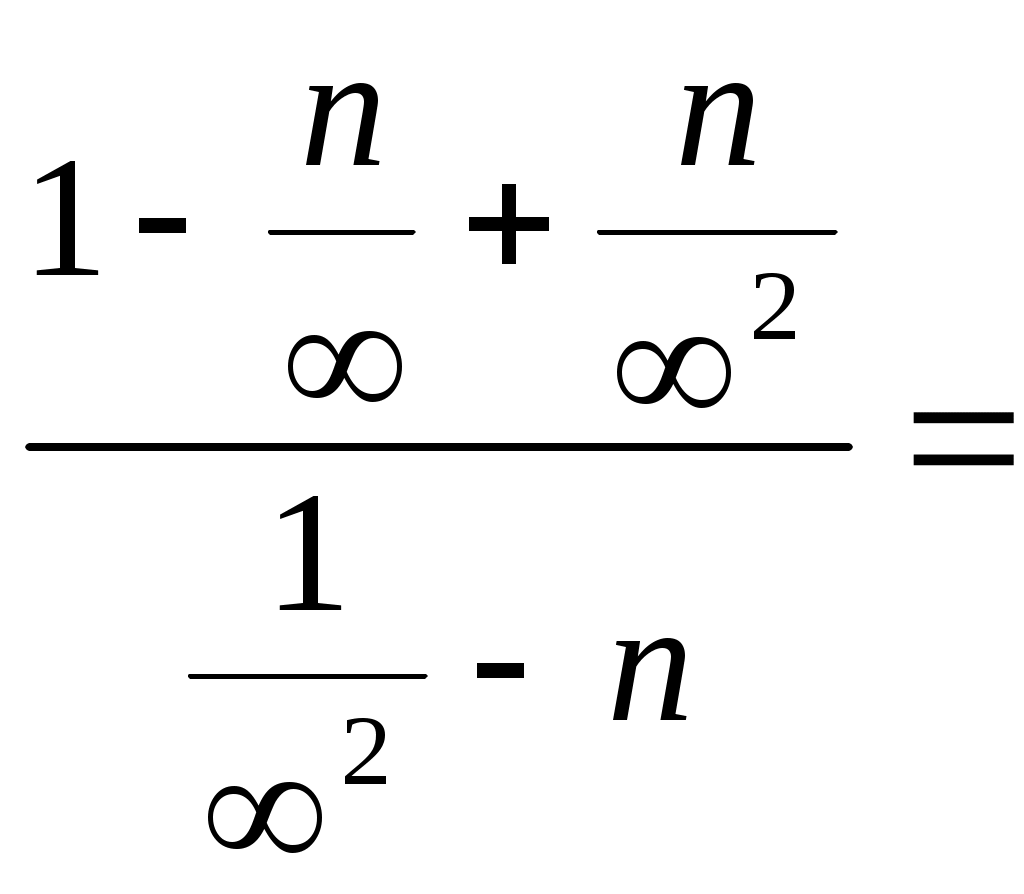 б) в) г) Задача 8. Исследуйте функцию на непрерывность графически. Определите характер точек разрыва с помощью односторонних пределов. Варианты 1-15. 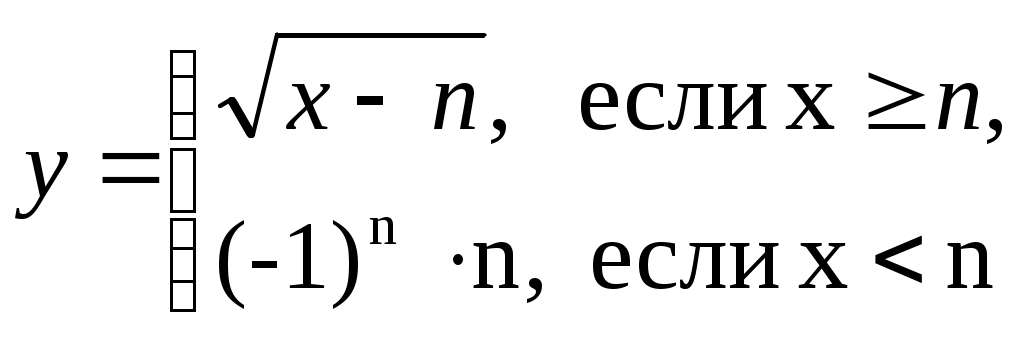 Решение 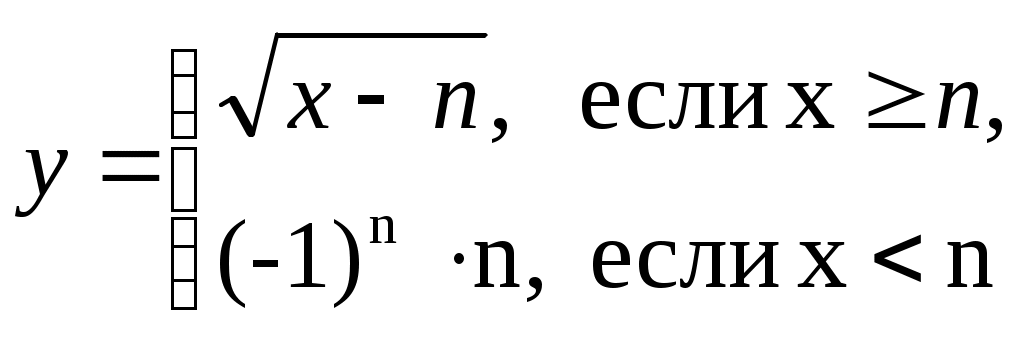 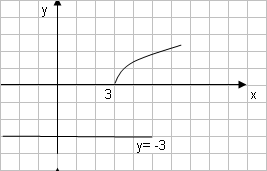 Односторонние пределы конечны и не равны, поэтому x=n=3 – точка разрыва 1 рода. Задача9*. Запишите комплексное число в алгебраической, тригонометрической. Варианты 1-15. Решение Алгебраическая форма: Тригонометрическая форма: z=1(cos(-90o)+isin(-90o)) z=cos90o - isin90o Задача 10. Найдите производные и дифференциалы 1 порядка. Варианты 1-5, 11-20. а) у = (n-2x)e n-x, б) y = ln Решение а) Применим правила дифференцирования произведения и сложной функции: у / = (n-2x)/ e n-x + (n-2x) (e n-x ) / = -2 e n-x + (n-2x) e n-x (n-x)/ = = -2 e n-x + (n-2x) e n-x (-1) =(2x-n-2) e n-x = (2x-5) e 3-x dy=f /(x)dx= (2x-5) e 3-x dx б) Применим правила дифференцирования частного и сложной функции: 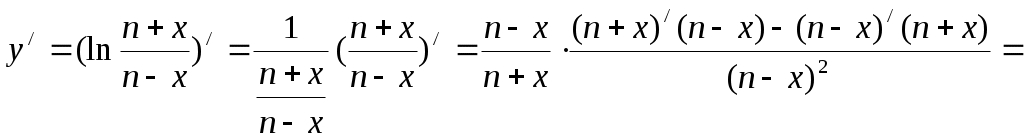 dy=f /(x)dx= Задача 11. Найдите пределы по правилу Лопиталя: Варианты 1-5 а) Решение а) б) 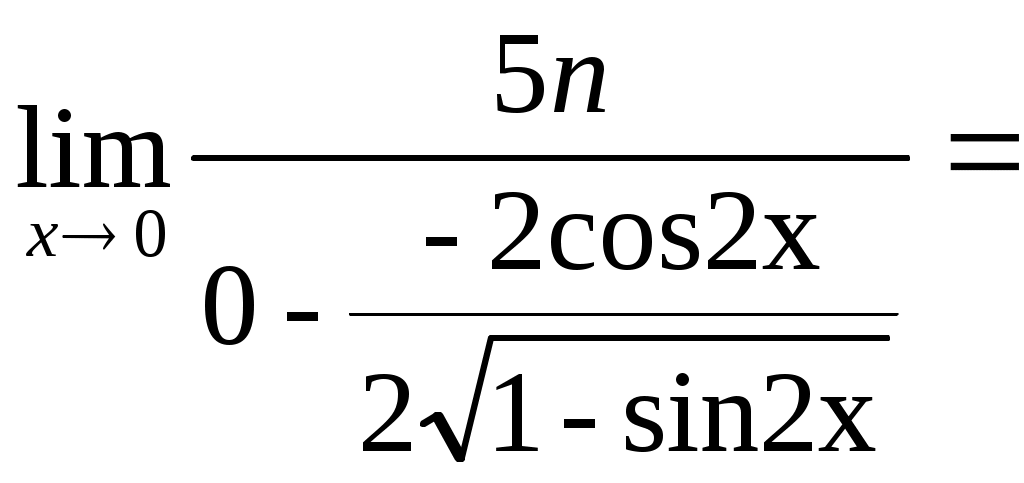 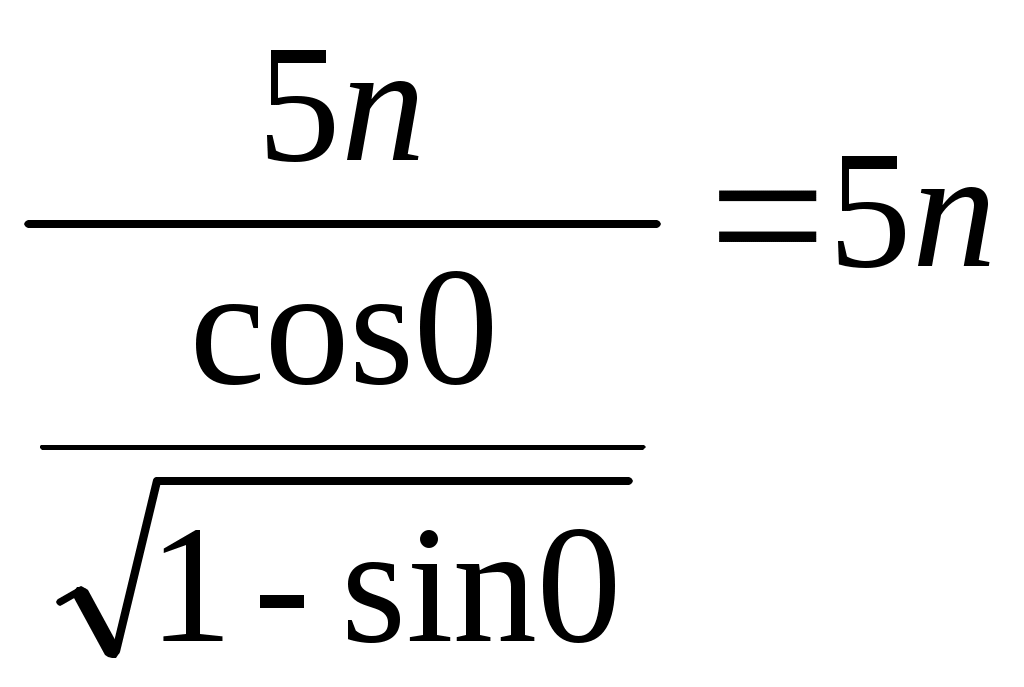 =15 =15 Задача 12. Найдите уравнение касательной к графику функции Сделайте чертеж. Решение Сделаем чертеж 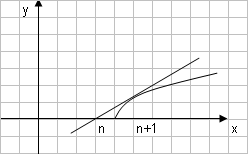 Уравнение касательной к графику функции y=f(x) в точке Mо(хо,уо) имеет вид: у-f(xо)= f ’(xo)(х-хо). f(xо)= f ’(xo) = Уравнение касательной: у-1= 0,5(х-n) y=0,5x+1-0,5n = 0,5x-0,5 Задача 13. Найдите наибольшее и наименьшее значения функции Решение Найдем производную функции: Производная не обращается в 0. Производная не определена при x+1=0, откуда x=-1 – критическая точка вне отрезка [0,n]. Таким образом, наибольшее и наименьшее значения функции могут быть только на концах отрезка: Наибольшее значение равно f(n)=0. Наименьшее значение равно f(0)= -3. СПИСОК ЛИТЕРАТУРЫБугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление, М., 1988 Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов, ч.1, М.,1986 Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов: учебн. пособие для вузов. – М.: ЮНИТИ , 2004. – 474 с. Черненко В. Д. Высшая математика в примерах и задачах: учебное пособие для вузов. В 3 т.: Т. 1. – СПб.: Политехника, 2003. – 703 с. |
