Математика лекции. Лекции. Тема Дифференциальное интегральное исчисление
 Скачать 184.94 Kb. Скачать 184.94 Kb.
|
|
Раздел 1. Математический анализ. Тема 1.1. Дифференциальное интегральное исчисление. 1. Функции одной независимой переменной. Пусть даны два множества произвольной природы Х и У, состоящие из произвольных элементов х и у. Определение. Если каждому эл-ту х 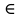 Х по некоторому правилу f поставлен в соответствие элемент у Х по некоторому правилу f поставлен в соответствие элемент у 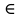 У, то говорят что на множестве Х определена функция со значениями в множестве У. У, то говорят что на множестве Х определена функция со значениями в множестве У.Пишут: у = f(х) Х – независимая переменная или аргумент; У – зависимая переменная или функция. Множество Х - область определения функции (Д(f)); Множество У - область значений функции (Е(f)). Пример: 1) у = 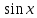 : Д(f) = ( : Д(f) = ( Е(f) = 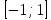 2) у = 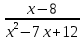 = = 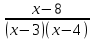 : :Д(f) = ( 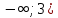  (3; 4) (3; 4) (4; + (4; +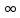 ) )Е(f) = (- 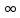 ; + ; +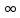 ). ).Определение. Частным значением функции у =f(х) при х = хо , хо 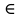 Х наз. То значение у, которое соответствует данному значению хо . Х наз. То значение у, которое соответствует данному значению хо .Обозначается: f(хо). Пример: Выч-ть частное значение функции V = 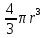 при R = 3 при R = 3V(3) = 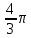  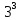 = 36 = 36 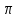 Существует несколько способов задания функции: 1) аналитический – функциональная зависимость между переменными х и у выражается в виде формулы, которая указывает совокупность тех математических операций, которые должны быть выполнены, чтобы по заданному значению аргумента найти соответствующее значение функции. Пример: 1) у = 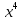 ; 2) S = Vt; 3) у = ; 2) S = Vt; 3) у = 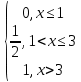 2) табличный – функциональная зависимость между переменными описывается в виде таблицы величин – аргумента и функции.
3) графический – если функция задана в виде формулы у = f(х), то ее графиком является мн-во точек плоскости, координаты которых удовлетворяют соотношению у = f(х). Пример: у = 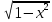 - графиком является полуокружность. - графиком является полуокружность. 4) словесный – функция описывается правилом составления. Пример: функция Дирихле f(х) = 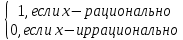 2. Предел функции. Определение 1. (по Гейне). Если для любой последовательности х1, х2, . . .; хп , . . , входящих в область определения функции и сходящихся к а, но отличных от а, соответствующая последовательность значений функции f1 (х), f2 (х), . . ., fп (х), . . . сходится и притом всегда к одному и тому же числу А, то говорят, что функция f(х) стремится к А при х, стремящемся к а, а число А называют пределом функции f(х) в точке а или ее предельным значением в этой точке. Другими словами, А – предел функции f(х) при х 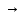 а, если из условия а, если из условия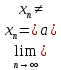 а) всегда следует равенство а) всегда следует равенство 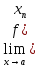 ) = А ) = АОпределение 2 (по Коши). Число А называется пределом функции f(х) при х 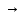 а (или в точке а), если для любого наперед заданного сколь угодно малого положительного числа Е можно найти такое положительное число б, что для всех значений х, входящих в область определения функции, отличных от а а (или в точке а), если для любого наперед заданного сколь угодно малого положительного числа Е можно найти такое положительное число б, что для всех значений х, входящих в область определения функции, отличных от а 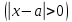 и удовлетворяющих условию и удовлетворяющих условию 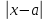  б, имеет место неравенство: б, имеет место неравенство: 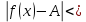 Е. Е.Пример. Доказать, что 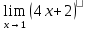 = 6 = 6Док – во: 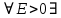 б (Е) б (Е)  0 : 0 : 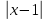  б б 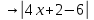  Е ; Е ; 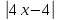  Е ; 4 Е ; 4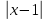  Е; Е;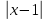  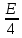 Сравнивая 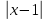  б и б и 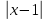  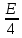 заключаем, что в качестве б можно взять заключаем, что в качестве б можно взять 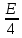 . .Например, при Е = 1 : б = 0,25 при Е = 0,1 : б = 0,025, т. е. 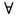 Е Е 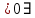 б (Е) б (Е) 0 0Правила предельного перехода: Рассмотрим функции у = f1 (х) и у = f2 (х), которые при х 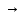 х0 имеют пределы, т.е. х0 имеют пределы, т.е.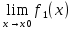 = А1 = А1 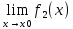 = А2 = А2 Теорема 1 (о пределе алгебраической суммы). Предел алгебраической суммы двух функций, имеющих пределы при х 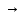 х0 , равен алгебраической сумме пределов этих функций, т.е. х0 , равен алгебраической сумме пределов этих функций, т.е.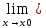 (f1 (х) (f1 (х) 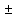 f2 (х)) = f2 (х)) = 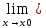 f1 (х) f1 (х) 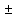 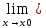 f2 (х) = А1 f2 (х) = А1 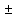 А2 А2Теорема 2 (о пределе произведения). Предел произведений двух функций, имеющих пределы при х 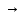 х0, равен произведению пределов этих функций, т. е. х0, равен произведению пределов этих функций, т. е. 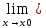 (f1 (х) (f1 (х)  f2 (х)) = f2 (х)) = 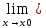 f1 (х) f1 (х)  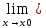 f2 (х) = f2 (х) = 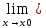 f2 (х) f2 (х)  А2 А2Следствие. 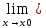 (с f (х)) = с (с f (х)) = с  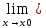 f (х), с – const. f (х), с – const.Теорема 3 (о пределе частного). Предел частного двух функций, имеющих пределы при х 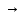 х0, равен частному пределов этих функций, если х0, равен частному пределов этих функций, если 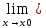 f2 (х) = А2 f2 (х) = А2 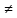 0, т.е. 0, т.е.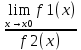 = = 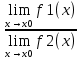 = = 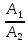 Пример: 1) 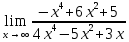 = = 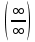 = разделим числитель и знаменатель на старшую степень х : х4 = разделим числитель и знаменатель на старшую степень х : х4 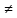 0 при х 0 при х 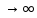 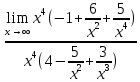 = = 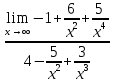 = = 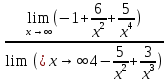 = = 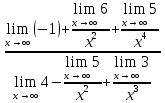 = = 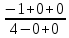 = = 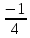 2) 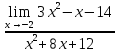 = =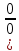 ) = разложим числитель и знаменатель на множители ) = разложим числитель и знаменатель на множители= 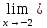 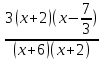 = = 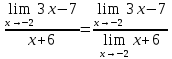 = = 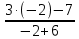 = = 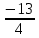 = - = - 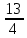 3) 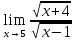 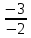 = = 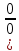 ) = умножим числитель и знаменатель на сопряженные выражения ) = умножим числитель и знаменатель на сопряженные выражения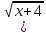 +3) +3) ( (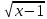 +2) +2)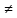 0 0= 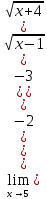   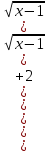 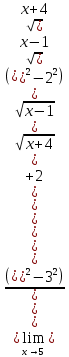 = = 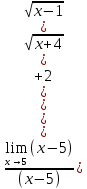 = = 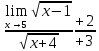 = = 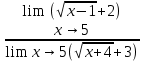 = = 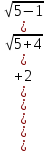 = = 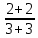 = = 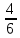 = = 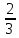 4) 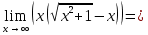 умножим и разделим на сопряженный умножим и разделим на сопряженный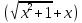 == 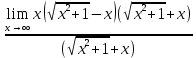 = = 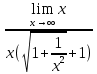 = = 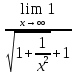 = = 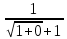 = = 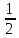 Первый замечательный предел. Теорема. Рассмотрим функцию f(х) = 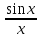 . Эта функция в точке х = 0 не определена, тем не менее ее предел при х . Эта функция в точке х = 0 не определена, тем не менее ее предел при х 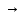 0 0 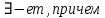 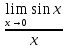 = 1 = 1Док-во: 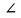 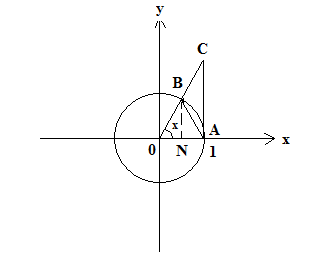 АОВ = х, 0 АОВ = х, 0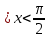 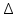 АОВ АОВ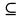 сектор АОВ сектор АОВ  АОС АОС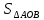 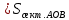 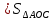 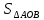 = = 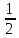 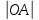  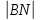 = = 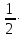 1 1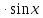 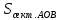 = = 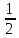 х х  ОА2 = ОА2 = 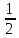 х х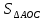 = = = = 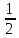 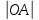  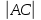 = = 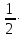 1 1 tg х tg х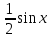 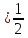 х х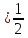 tg х tg х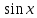 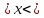 tg х; tg х; 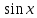  (т.к. 0 (т.к. 0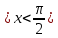 1 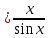 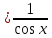 ; 1 ; 1 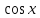 ; ;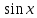 = =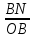 = BN; = BN; 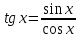 = = 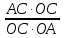 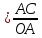 = АС = АС1 – 1  1 – 1 – 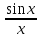 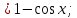 0  1 – 1 – 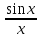 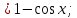 0  1 – 1 – 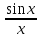  2 2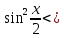 2 ( 2 ( 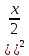 (т. к. (т. к. 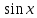 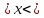 tg х); tg х); 0  1 – 1 – 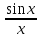 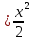 выполняется 0 выполняется 0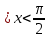 Если 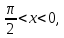 то 0 то 0  - - 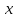 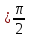 и выполняется и выполняется0  1 – 1 –    0  1 – 1 – 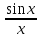 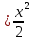 т. о. , для 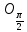 (0) =( - (0) =( - 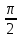 ; ; 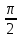 ) ) 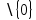 выполняется выполняется 0  1 – 1 – 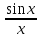 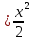 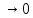 при х при х 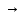 0 0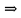 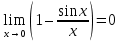 или или 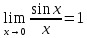 теорема доказана. теорема доказана.Пример: 1) 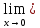 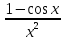 = = 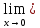  = = 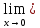 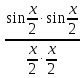 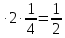 ; ;2) 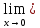 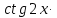 tg 3х = tg 3х = 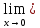 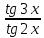 = = 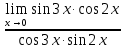 = = 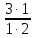 = = 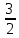 3) 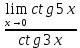 = = 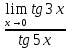 = =  4) 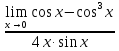 = = 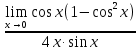 = = 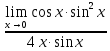 = = 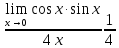 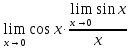 = = 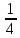 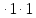 = = 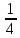 Второй замечательный предел. (лекция) Пример: 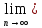 ( (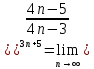 ( (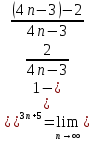 = = Замена: - 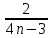 = = 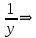 4 4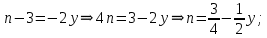 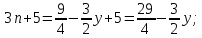 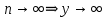 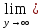 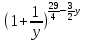 = = 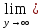 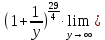 ( (  = 1 = 1 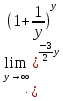 = == 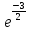 = = 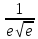 Д/з: 1) 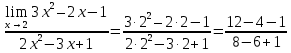 = = 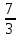 Второй замечательный предел. Доказать что последовательность 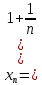 сходится. сходится. Предел этой последовательности следуя математическому Эйлеру обозначается буквой 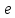 и называется «числом Эйлера». и называется «числом Эйлера». Обоснуем следующее равенство  = = 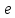 Рассмотрим функцию 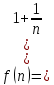 целочисленного аргумента целочисленного аргумента 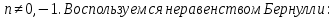 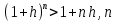 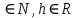 и и 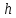 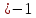 Тогда для любого 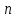 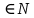 выполняется: выполняется:1 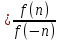 = = 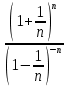 =(( =(( 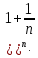 ( (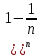 = ( = (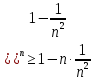 = 1 - = 1 - 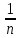 С другой стороны 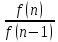 = = 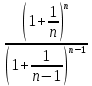 = ( = (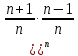 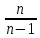 = ( = ( 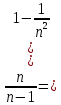 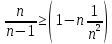 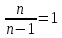 Аналогично проверяется, что 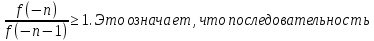 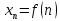 возрастает, последовательность возрастает, последовательность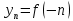 убывает и 1 убывает и 1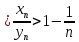 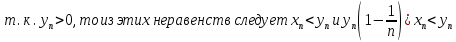 Вычитая из 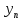 члены последнего неравенства получаем 0 члены последнего неравенства получаем 0 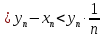 т.о.  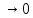 и последовательности и последовательности 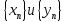 имеют общий предел, который и обозначается имеют общий предел, который и обозначается 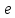 . .т.о. 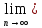 ( ( 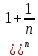 = = 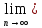 ( ( 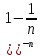 = =  1. Непрерывность функций одной независимой переменной. 2. Производная. Геометрический смысл. 3. Исследование функций. |
