Математика лекции. Лекции. Тема Дифференциальное интегральное исчисление
 Скачать 184.94 Kb. Скачать 184.94 Kb.
|
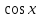 . Здесь характ-ое уравнение k2 - 1 = 0 имеет корни k1 =1, k2 = -1. Общее решение однородного уравнения имеет вид: . Здесь характ-ое уравнение k2 - 1 = 0 имеет корни k1 =1, k2 = -1. Общее решение однородного уравнения имеет вид:У = С1ех + С2е – х В правой части стоит произведение многочлена нулевой степени, показательной и тригонометрической функции, так что 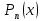 = 3, = 3, 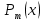 = 0, S = 0. Т.к. число = 0, S = 0. Т.к. число α + iβ = 2 + i1 не является корнем характ-го уравнения, то  r = 0 и частное решение ищем в виде: r = 0 и частное решение ищем в виде: 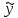 = е2 х (А = е2 х (А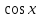 + В + В 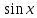 ). ).Дифференцируя и подставляя в уравнение, получим: (2А + 4В) 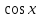 + (2В – 4А) + (2В – 4А) 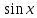 = 3 = 3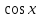 2А + 4В = 3, - 4А + 2В = 0 ⟹ А = 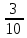 , В = , В =  . .Т.о. частное решение 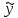 = е2 х ( = е2 х (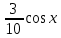 + + 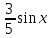 ), а общее решение ), а общее решение у = 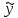 +У = е2 х ( +У = е2 х (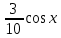 + + 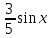 ) + С1ех + С2е- х . ) + С1ех + С2е- х .РАЗДЕЛ 2. Основы дискретной математики. Тема 2.1. Множество и отношения. Свойства отношений. Операции над множествами. 1. Понятие множества. Операции над множествами. Свойства. 2. Понятие отношения. Свойства отношений. 1). Понятие множества является одним из основных в математике. Оно относится к числу первичных, неопределяемых через более простые. Слова совокупность, семейство, система, набор и т.п. – являются синонимами слова множество. Объекты, из которых состоит множество, называются его элементами, или точками. Множества обозначаются большими, а их элементы малыми буквами. Если х – элемент множества Х, то пишут х ∈ Х , если нет – то х ∉ Х. Если х1,. . ., хn некоторые элементы, то запись Х = 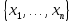 означает, что множество Х состоит из элементов х1,. . ., хn. означает, что множество Х состоит из элементов х1,. . ., хn. Пусть Х и У два множества. Если Х и У состоят из одних и тех же элементов, то говорят, что они совпадают, и пишут Х = У. Если в Х нет элементов не принадлежащих У, то говорят что Х содержится в У , или что Х является подмножеством множества У. В этом случае пишут Х ⊂ У или У ⊃ Х. Множество, не содержащее ни одного элемента, называется пустым и обозначается ∅. Множество с установленным порядком расположения элементов называют упорядоченным. Упорядоченные множества записывают внутри круглых скобок. Введем операции над множествами. Определение: Объединением двух множеств А и В называется множество, обозначаемое А ∪ В которому принадлежат либо элементы множества А, либо – В, т.е. х ∈ А ∪ В = (х ∈ А) ⋁ (х ∈ В) А ⋃ В 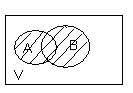 Определение: Пересечением множеств А и В называется множество, обозначаемое А ⋀ В, которому принадлежат те элементы из А и В, которые входят одновременно в оба множества, т.е. х ∈ А ⋂ В = (х ∈ А) ⋀ (х ∈ В) А ⋂ В 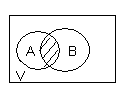 Определение: Разностью между множествами А и В, называется множество, обозначаемое А∖ В, которому принадлежат те элементы множества А, которые не вошли в множество В, т.е. х ∈ А∖ В = ( х ∈ А) ⋀ (х ∉ В) А ∖ В 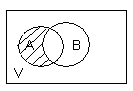 Определение: Дополнением множества А до фундаментального множества называется множество 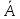 , которому принадлежат все элементы, кроме элементов, принадлежащих А. , которому принадлежат все элементы, кроме элементов, принадлежащих А.х ∈ 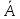 ⟺ х ∉ А ⟺ х ∉ А 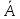 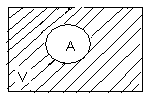 Свойства операций над множествами. Пусть задано фундаментальное множество ⋁. Тогда ∀ А, В, С ∈ V выполняются следующие свойства: 1. А∪А = А∩А = А (идемпотентность) 2. А∪В = В∪А, А∩В = В∩А (коммутативность) 3. А∪(В∩С) = (А∪В) ∩ (А∪С) А∩(В∪С) = (А∩В) ∪ (А∩С) (дистрибутивность) 4. А∪(В∪С) = (А∪В) ∪ С А∩(В∩С) = (А∩В) ∩ С (ассоциативность) 5. (А∩В) ∪ А = А, (А∪В) ∩А = А (поглощение) 6. А∪∅ = А, А ∩ ∅ = ∅ (свойства нуля) 7. А∪⋁=⋁, А∩⋁=А (свойства единицы) 8. 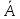 = А (инволютивность) = А (инволютивность)9. 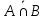 = = 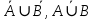 = = 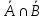 (законы де Моргана) (законы де Моргана)10. А∪ 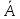 = ∨, А∩ = ∨, А∩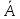 = ∅ (свойства дополнения) = ∅ (свойства дополнения)11. А∖В = А∩ 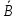 (выражение для разности) (выражение для разности)2). Определение: Прямым произведением множества А на множество В называют множество Р, состоящее из всех упорядоченных пар (а,в), где а ∈ А, в ∈ В. Обозначается Р = АхВ. Бинарные отношения – это отношения, которые определены для пар элементов данного множества. 1.Если α – множество людей, то для элементов х ∈ α у ∈ α можно рассматривать отношение «х есть отец у». 2. Для элементов х ∈ R, у ∈ R можно рассматривать отношение «х < у». 3. Если Т – множество треугольников, то для элементов х ∈ Т, у ∈ Т можно рассматривать отношение «х подобен у». Обратим внимание на следующее: а) бинарное отношение имеет место не для произвольной пары элементов из данного множества, а лишь для некоторых пар; б) если элемент х находится в данном отношении к элементу у, то у не находится в этом отношении к элементу х. Это означает, что отношение следует рассматривать не просто для пар 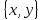 , а для упорядоченных пар (х; у); , а для упорядоченных пар (х; у);в) каждое отношение между элементами данного множества характеризуется совокупностью упорядоченных пар элементов данного множества, для которых это отношение имеет место. Определение: Отношением ρ называется упорядоченная пара множеств, первая компонента которой есть подмножество декартового квадрата второй компоненты Ρ = (Р;М), Р⊂М2 Множество М называется множеством задания этого отношения, Р – графиком. Если (х;у) ∈ Р, то говорят что х находится в отношении ρ к у и пишут хρу или ρху. Определение: отношение ρ называется рефлексивным, если для любого х ∈ М верно хρх. Определение: Отношение ρ называется симметрическим, если для всех х ∈ М, у ∈ М верно: хρу⟹ уρх. Определение: Отношение ρ называется транзитивным, если для любых х ∈ М, у ∈ М, z ∈ М верно: хρу⋀уρz. Определение: Отношение ρ называется отношением эквивалентности, если оно рефлексивное, симметрическое и транзитивное. Тема 2.2. Основные понятия теории графов. 1. Понятие графа. Основные определения. 2. Операции над графами. 1) Определение 1: Графом G = (V,X) называется пара двух конечных множеств: множество точек и множество линий, соединяющих все или часть точек. Определение 2: Точки называются вершинами или узлами графа, линии ребрами. Определение 3: Если ребро графа соединяет две его вершины, то говорят, что это ребро им инцидентно. Определение 4: Две вершины графа называются смежными, если существует инцидентное им ребро. Определение 5: Ребро, у которого начало и конец совпадают, называется петлей. Определение 6: Два ребра называются смежными, если они имеют общую вершину. Определение 7: Граф G называется полным, если любые две его различные вершины соединены одним и только одним ребром. Определение 8: Если вершина графа имеет только одну смежную ей вершину, то она называется висячей. Определение9: Если вершина графа не соединена ни с одной другой, то она называется изолированной. Определение 10: Граф, состоящий из изолированных вершин, называется нуль графом. Для него Х = ∅. Определение 11: Если ребра графа соединяют любые пары вершин, то граф называется неориентированным. Его ребра изображаются линией. 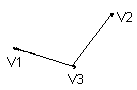 Определение 12: Если ребро графа соединяют упорядоченные пары вершин, то граф называется ориентированным. Ребра ориентированного графа называются дугами и изображаются линией со стрелкой. 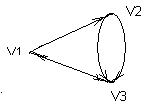 Определение 13: Вершина, из которой выходит дуга, называется началом, вершина, в которую входит дуга – концом (графически она указана стрелкой). 2). Пусть даны графы G1 = (V1, X1) и G2 = (V2, X2). 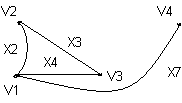 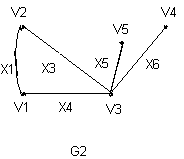 G1 Определение 1: Объединением графов G1 и G2 называется граф G = G1∩ G2, множество вершин которого V = V1 ∪ V2, а множество ребер Х = Х1 ∪ Х2. 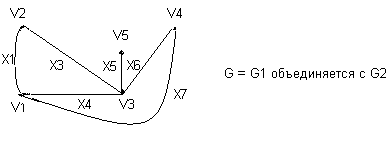 Определение 2: Пересечением графов G1 и G2 называется граф G = G1∩ G2, для которого Х = Х1 ∩ Х2 - множество ребер, а V = V1 ∩ V2 – множество вершин. 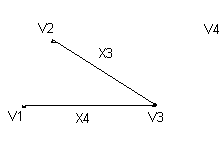 Определение 3: Подграфом графа G = (V, Х) называется граф G1 = (V1, Х1) все вершины и ребра которого являются подмножествами множества вершин и ребер исходного графа. Определение 4: Кольцевой суммой графов G1 и G2 называется граф G = G1  порожденный множеством вершин V = V1 ∪ V2 и множеством ребер Х = (Х1 ∪ Х2) ∖ порожденный множеством вершин V = V1 ∪ V2 и множеством ребер Х = (Х1 ∪ Х2) ∖( Х1 ∩ Х2), т.е. множество ребер, содержащихся либо в G1, либо в G2, но не в G1∩ G2. 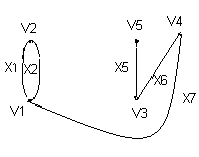 G = G1 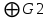 Раздел 3. Основы теорий вероятностей и математической статистики. Тема 3.1. Вероятность. Теорема сложения вероятностей. 1. Основные определения теории вероятностей. 2. Понятие вероятности события. 3. Теорема сложения вероятностей. 1). Понятие события является одним из основных для теории вероятностей. Под событием понимается явление, которое осуществляется в результате какого-либо комплекса действий. Комплекс действий называется опытом или испытанием. Определение: Случайным называется событие, которое может произойти или не произойти в результате некоторого опыта. Определение: Событие называется достоверным, если оно обязательно произойдет в результате опыта. Определение: Событие называется невозможным, если оно не может произойти в результате данного опыта. Определение: События А и В называются совместными если в результате данного испытания появление одного из них не исключает появление другого, и несовместными в противном случае. Определение: Два события А и 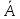 называются противоположными или взаимно дополнительными, если непоявление одного из них в результате данного испытания влечет появление другого. называются противоположными или взаимно дополнительными, если непоявление одного из них в результате данного испытания влечет появление другого.Определение: Если группа событий такова, что в результате испытания обязательно должно произойти, хотя бы одно из них и любые два из них несовместны, то это группа событий называется полной группой событий. Определение: Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного их них в результате испытания. Определение: Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий в результате испытания. Определение: События называются совместными в совокупности, если каждое из них и и произведение остальных являются совместными событиями. 2 ). Определение: Вероятность события, это численная мера объективной возможности его появления обозначается Р(А) – вероятность события А. Для определения вероятности события, например события А, применяется классическая формула вероятности Р(А) = 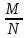 (1), (1),где М – число исходов, благоприятствующих событию А, N – число всех исходов испытания. Пример: Бросаются два игральных кубика. Какова вероятность того, что сумма выпавших очков равна 7? Решение: Два кубика по правилу умножения могут упасть 6 ∙ 6 = 36 способов. Т.е. возможно 36 исходов, которые соответствуют бросанию двух кубиков. Т.к. кубики симметричны, все эти исходы равновозможны и образуют полную группу несовместных событий. Поэтому число всех исходов бросания двух кубиков N = 36. Пусть событие А заключается в выпадении суммы очков равной 7. Число благоприятствующих исходов М = 6. Тогда по (1) Р(А) = 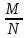 = = 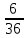 = = 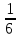 3). Теорема: Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий. Док-во: Введем обозначение: N – общее число исходов испытания; М – число исходов, благоприятствующих событию А; α – число исходов, благоприятствующих событию В. Тогда Р(А) = 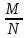 , Р(В) = , Р(В) = 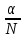 . .Т.к. события А и В несовместны, то нет таких исходов, которые были бы благопр –ми и событию А и событию В одновременно. Поэтому события А + В благоприятствуют М + α исходов и Р(А + В) = = 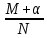 = = 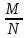 + + 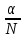 = Р(А) + Р(В), что и требовалось доказать. = Р(А) + Р(В), что и требовалось доказать.Теорема: Вероятность появления одного из нескольких попарно несовместных событий равна сумме вероятностей этих событий, т. е. Р(А1 + А2 + . . .+ Аn) == Р(А1) + Р(А2) +. . . + Р(Аn) или Р( 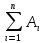 ) = ) = 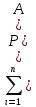 ) )Следствие 1: Сумма вероятностей попарно несовместных событий А1 , А2 , . . .+ Аn, образующих полную группу равно 1, Р(А1) + Р(А2) +. . . + Р(Аn) = 1 Следствие 2: Сумма вероятностей противоположных событий равна 1, т.е. Р(А) + Р( 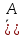 = 1 = 1Теорема: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления, т. е. Р(А + В) = Р(А) + Р(В) – Р(АВ) Определение: Условной вероятностью РА(В) называется вероятность события В, вычисленная в предположении, что событие А уже наступило. Теорема(умножения вероятностей): Вероятность совместного появления двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ) = Р(А) ∙ РА(В) Определение: Два события называются независимыми, если появление любого из них не изменяет вероятность появления другого, т.е. Р(А) = ∙ Рв(А) или Р(В) = РА(В) Теорема: Вероятность совместного появления двух независимых событий равна произведению их вероятностей, т. е. Р(АВ) = Р(А) ∙ Р(В). |
