Математика лекции. Лекции. Тема Дифференциальное интегральное исчисление
 Скачать 184.94 Kb. Скачать 184.94 Kb.
|
|
1) Пусть у =  определена на промежутке Х и некоторой окрестности т. определена на промежутке Х и некоторой окрестности т.  содержащейся в Х. содержащейся в Х.Определение: Функция у =  называется непрерывной в т. называется непрерывной в т.  если если Это означает что: Это означает что:1. Определено значение 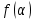 , т.е. , т.е.  2.  . .3. Выполняется равенство  Свойства функций непрерывных в точке. 1. Если  хо , то в этой точке непрерывны также хо , то в этой точке непрерывны также 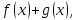  и и  (если (если  2. Если функция у = 2. Если функция у =  и функция и функция  непрерывна в т. непрерывна в т. 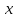 о причем о причем  = =  (х0 ), то сложная функция (х0 ), то сложная функция  непрерывна в т. хо. непрерывна в т. хо.3. Если функция у =  непрерывна в т. непрерывна в т. то она ограничена в некоторой окрестности то она ограничена в некоторой окрестности т. хо. 4. Если функция у =  непрерывна в т. хо то эта функция сохраняет знак значения непрерывна в т. хо то эта функция сохраняет знак значения  хо) в некоторой окрестности т. хо. хо) в некоторой окрестности т. хо.Определение: функция у =  на множестве х, если она непрерывна в каждой т. этого множества т.е. ( на множестве х, если она непрерывна в каждой т. этого множества т.е. (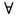 х0 х0   о). о).2) Определение: Если существует конечный предел отношения  приращения функции к приращению аргумента, то этот предел называется производной функции приращения функции к приращению аргумента, то этот предел называется производной функции у =  в т. в т.  Обозначается 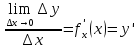 (х) = (х) =  = =  Операция вычисления производной называется дифференцированием. Геометрический смысл производной: tg а =  Производная в точке равна тангенсу угла наклона касательной в этой точке к оси ох .  Запишем уравнение касательной Запишем уравнение касательной у – у0 = к (х - 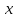 о) о)АВ = у – у0 , М0В = х - 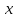 о оtg а =   Определение: (правила дифференцирования): если функции u = u(х),  = =  дифференцируемы в . дифференцируемы в . 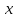 о, то в этой точке дифференцируемы также u + о, то в этой точке дифференцируемы также u +  u u   , u : , u :  (если (если  о) о)  Причем (u +  ’ = u’ + ’ = u’ +  (u   ’= u’ ’= u’  u u  ’ ’(  )’ = )’ =  3) 1. Находим  (f) функции. (f) функции.2. Определяем особенности функции (четность, нечетность, периодичность). 3. Точки пересечения с осями координат и интервалы знакопостоянства функции. 4. Исследуем поведение функции на границах области определения.(асимптоты). 1. Если   = =  то х = а – вертикальная асимптома; то х = а – вертикальная асимптома;2. если  = A, то у = А – горизонтальная асимптома; = A, то у = А – горизонтальная асимптома;3.если  – kx) = b, то у = kx + b – наклонная асиптома. – kx) = b, то у = kx + b – наклонная асиптома.5. Исследуем на монотонность и экстремизмы. 6. Исследуем на вогнутость и точки перегиба. 7. Строим схематический график. Пример: Исследовать функцию у =  1.  2. Функция не является ни четной, ни нечетной. Функция не является периодической. 3. Пересечение с  : х = 0, у = -2. Точка (0; -2) - точка пересечения с осью Оу. : х = 0, у = -2. Точка (0; -2) - точка пересечения с осью Оу.С Ох :  = 0; = 0;  Точек пересечения с Ох нет.  4. Наклонные асимптомы k =  = =   = 1 = 1b =  ( ( - kx) = - kx) =  ( ( - х) = -1 - х) = -1у = kx + b = 1  х – 1 – наклонная асимптома. х – 1 – наклонная асимптома.Вертикальная асимптома.  = =  , значит х = 1 вертикальная асимптома. , значит х = 1 вертикальная асимптома.6. у’ =  = =   = 0; х1 = 0, х2 = 2 = 0; х1 = 0, х2 = 2 7. Строим график.  1. Определение неопределенного интеграла. Св – во. 2. Определение определенного интеграла. 3. Функции нескольких переменных. Частные производные. 1. Определение: Если функция  имеет первообразную F(х), то выражение F(х) + С, где С имеет первообразную F(х), то выражение F(х) + С, где С 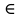 R называется неопределенным интегралом функций R называется неопределенным интегралом функций  и обозначается символом: и обозначается символом: Т.о по определению  = F(х) + С, где F’(х) = = F(х) + С, где F’(х) = Свойства неопределенного интеграла. 1. (  )’ = )’ =  или d или d  = =  2.  = k = k 3.  + + 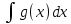 4. Метод интегрирования заменой переменной  = =   φ’(t) dt, где х = φ (t) и все интегралы существуют. φ’(t) dt, где х = φ (t) и все интегралы существуют.2.Определение. Пусть функция у =  определена на отрезке определена на отрезке  . Разобьем этот отрезок на n частей точками a = xо< x1 < . . . . Разобьем этот отрезок на n частей точками a = xо< x1 < . . .  мелкость разбиения. мелкость разбиения.Выберем производную точку ξi ∈  и составим интегральную сумму δ = и составим интегральную сумму δ =  Если существует и конечен  , то он называется определенным интегралом функции , то он называется определенным интегралом функции  на отрезке на отрезке  и обозначается и обозначается  Таким образом по определению  = =  Геометрический смысл определенного интеграла: Определенный интеграл от функции  ≫ 0 на отрезке ≫ 0 на отрезке  численно равен площади криволинейной трапеции, ограниченной сверху графиком численно равен площади криволинейной трапеции, ограниченной сверху графиком 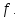 Теорема. Пусть функция у =  определена и непрерывна на определена и непрерывна на  , тогда определенный интеграл от , тогда определенный интеграл от  на отрезке на отрезке  вычисляется по следующей формуле: вычисляется по следующей формуле: = F(b) – F(a), где F(x) первообразная функции = F(b) – F(a), где F(x) первообразная функции  Эта формула называется формулой Ньютона – Лейбница и сокращенно записывается следующим образом:  = =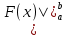 , где F(x) – первообразная функции , где F(x) – первообразная функции  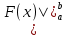 = F(b) – F(a) = F(b) – F(a)3. Определение. Переменная z называется функцией независимых переменных х, у в множестве М, если каждой паре (х,у) по некоторому правилу или знаку ставится в соответствие единственное значение z. z =  z = φ(x,y) z = z(х,у) и т.д. z = φ(x,y) z = z(х,у) и т.д.Определение: Пусть имеем независимых переменных х1, х2, . . . , х n принадлежащих множеству М. Если точку (х1, х2, . . . , х n ) обозначить через N, то функцию U=  (х1, х2, . . . , х n) иногда называют функцией т. N. (х1, х2, . . . , х n) иногда называют функцией т. N.Частные производные. Пусть функция U=  (х, у, z) определена в области D. (х, у, z) определена в области D.Возьмем точку М0 (х0, у0, z0)∈ D. Если у = у0, z = z0, то функция и будет зависеть от х. Тогда можно вычислить производную этой функции в т. х = х0, придадим х 0 приращение ∆ х, тогда 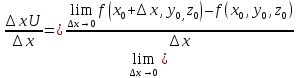 Эта производная называется частной производной функции  (х, у, z) по х в т. (х0, у0, z0). (х, у, z) по х в т. (х0, у0, z0).Частную производную обозначают:  , ,  , U’x и т.д. , U’x и т.д.Аналогично считая х и z постоянными, а у – переменной, рассмотрим предел   = =  Этот предел называется частной производной функции  (х, у, z) по у в т. (х0, у0, z0). (х, у, z) по у в т. (х0, у0, z0).Обозначается:  , ,  , U’у и т. д. , U’у и т. д.Аналогично определяется частная производная функции  (х, у, z) по z в т. (х0, у0, z0). (х, у, z) по z в т. (х0, у0, z0).Tема 1. 4. Ряды. 1. Понятие числового ряда. Положительные ряды. 2. Признак Доламберо. 3. Абсолютная и условная сходимость рядов. 4. Степенные ряды. Разложение элементарных функций в ряд Маклорена. 1. Определение: пусть а1, а2,. . . аn, . . . бесконечная последовательность чисел. Выражение а1+ а2 + . . . + аn +. . . называется числовым рядом с членами а1, а2,. . . аn, . . . аn называется п-ым членом ряда.  - сокращенная запись числового ряда. - сокращенная запись числового ряда.Определение: Для ряда а1+ а2 + . . . + аn +. . . результаты последовательного суммирования образуют последовательность частичных сумм:  1 = а1, 1 = а1,  2 = а1 + а2 , . . ., 2 = а1 + а2 , . . .,  n = а1 + а2 + . . . + аn n = а1 + а2 + . . . + аn Если последовательность частичных сумм  имеет конечный предел имеет конечный предел  , то он называется суммой ряда и обозначается , то он называется суммой ряда и обозначается  = а1 + а2 + . . . + аn + . . . или = а1 + а2 + . . . + аn + . . . или  = = Т.о. по определению  = =  Определение: Ряд  называется сходящимся, если он имеет сумму и расходящимся в противном случае. называется сходящимся, если он имеет сумму и расходящимся в противном случае. Теорема. (Необходимый признак сходимости числового ряда): Если ряд  сходится, то сходится, то 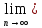 аn = 0. аn = 0.Определение: Положительным рядом называется ряд  С положительными членами аn > 0 ( n ∈ N)n = 1 Определение: Пусть дан ряд  = а1 + а2 + . . . + аn + аn + 1 + . . . (1) = а1 + а2 + . . . + аn + аn + 1 + . . . (1)Если в нем отбросить n первых членов, то ряд  (2) называется ряд остаток. (2) называется ряд остаток.2. |
