Математика лекции. Лекции. Тема Дифференциальное интегральное исчисление
 Скачать 184.94 Kb. Скачать 184.94 Kb.
|
Теорема: ( признак Доламбера): пусть для положительного ряда  существует предел D = существует предел D =  . Тогда при D > 1 ряд расходится, при D < 1 – сходится, при D = 1 – может вести себя как угодно. . Тогда при D > 1 ряд расходится, при D < 1 – сходится, при D = 1 – может вести себя как угодно.Док –во: Пусть D > 1. Тогда для О (D) = (1; + ∞) по определению предела   = D найдется номер n0 ∈ N, = D найдется номер n0 ∈ N,  ∈ О (D), т.е. ∈ О (D), т.е.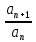 > 1, > 1,  > >  при n ≫ n0 при n ≫ n0при n = n0 :  > >  при n = n0 +1 :  > > > >  ≫ ≫  при n ≫ n0 при n ≫ n0Значит  ≫ 0, т.е. не вып – ся необходимый признак сходимости и ряд расходится. ≫ 0, т.е. не вып – ся необходимый признак сходимости и ряд расходится.Пусть D < 1. Рассмотрим произвольную q , которая удовлетворяет неравенству D 0 ≪ D < q < 1 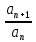 ∈ О (D), т.е. ∈ О (D), т.е. 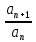 < q при n ≫ n0 ⟹ < q при n ≫ n0 ⟹  < q < q  при n ≫ n0 при n ≫ n0при n = n0 :  q q  при n = n0 +1 :  < <  q < q2 q < q2  при n = n0 + k :  < < qk qkт. к. q =  < 1, то ряд < 1, то ряд 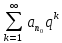 сходится, следовательно сходится ряд сходится, следовательно сходится ряд  также сходится, т. к. добавление конечного числа членов не влияет на сходимость. Для обобщенного гармонического ряда также сходится, т. к. добавление конечного числа членов не влияет на сходимость. Для обобщенного гармонического ряда  Вып – ся D=  = =  = = 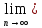 ( ( = 1 = 1Однако такой ряд может сходится при α > 1 и расходится при α ≪ 1. 3. Определение: Знакочередующийся ряд – это ряд, у которого чередуются положительные и отрицательные члены. Такой ряд записывается в виде a1 - a2 + a3 – a4 + . . . +(-1)n-1 an , где  или или (-1)n-1 an , где an > 0 (-1)n-1 an , где an > 0Теорема. (признак Лейбница): Если для знакочередующегося ряда  (-1)n-1 an последовательность (-1)n-1 an последовательность  монотонно убывает и стремится к 0, то ряд сходится. монотонно убывает и стремится к 0, то ряд сходится.Доказательство: Пусть Sn = a1 – a2 + a3 – a4 + . . . + (- 1)n – 1 an - n – ая частичная сумма ряда. Рассмотрим последовательность четных частичных сумм  т. к. т. к. S 2n = a1 – a2 + a3 – a4 +. . . + a2n-1 – a2n = a1 – ( a2 – a3) - . . . – (a2n - 2 - a2n – 1) - a2n < a1  возрастает, т.е. S 2n ≪ S2(n + 1). В самом деле возрастает, т.е. S 2n ≪ S2(n + 1). В самом деле S2(n + 1) = (a1 – a2 +. . . + a2n –n1 - a2n) + a2n + 1 -a2(n + 1) = S2n + (a2n + 1 - a2n + 2) ≫ S2n Ограниченная сверху, монотонно возрастающая последовательность  сходится, т.е. сходится, т.е. 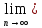 S2n = S. Отметим, что нечетные частичные суммы сходятся. S2n = S. Отметим, что нечетные частичные суммы сходятся.S 2n + 1 = (a1 – a2 + a3 + + a2n-1 – a2n) + a2n + 1 = S 2n + a2n + 1 → S ↓ ↓ S 0 Следовательно, 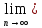 Sn = S, т. е. ряд сходится. Sn = S, т. е. ряд сходится.Определение: Ряд с членами произвольных знаков называется знакопеременным рядом. Определение: Ряд  an - называется абсолютно сходящимся, если сходится ряд абсолютных величин an - называется абсолютно сходящимся, если сходится ряд абсолютных величин  (*) расходится. (*) расходится.4. Определение: Ряд вида a0 + a1 x + a2 x2 + a3 x3 +. . . + an xn + . . . =  an xn (1) называется степенным рядом, где a1, a2 , . . . ,an - коэффициенты ряда. an xn (1) называется степенным рядом, где a1, a2 , . . . ,an - коэффициенты ряда.Определение: Совокупность тех значений х , при которых ряд (1) сходится называется областью его сходимости. Sn (x) = a0 + a1x + . . . + anxn - частичная сумма степенного ряда. S = S (x) =  anxn или f(x) = anxn или f(x) =  anxn - сумма ряда. anxn - сумма ряда.Для любой бесконечно дифференц – ой функции f(x) справедлива формула Маклорена: f(x) = f(0) +  x + x + x2 + . . . + x2 + . . . + xn + Rn (x), где xn + Rn (x), где Rn (x) = +  хn + 1 - остаточный член ряда Маклорена. хn + 1 - остаточный член ряда Маклорена.стр. 516 – 518 (самостоятельно). Тема 3.7. Обыкновенные дифференциальные уравнения. Определение. Уравнение вида (1) F (x, y, y’) =0, где х – независимая переменная, у – искомая функция, у’ - ее производная, называется дифф – ым уравнением 1-го порядка. Если уравнение (1) можно разрешить относительно у’, то его можно записать: у’ = f(x, у) (2) Уравнение (2) называется уравнением первого порядка, разрешенным относительно у’. Определение: Решением дифф –го уравнения 1-го называется функция у = φ (х), которая при подстановке в уравнение обращает его в тождество. График решения дифференциального уравнения называется интегральной кривой. Теорема Коши: Если в урав – ие у’ = f(x, у) функция f(x, у) и ее частная производная f у (x, у) определены и непрерывны в области G плоскости хОу, то какова бы ни была внутренняя т. (х0, у0) из G, существует ед-ое решение у = φ (х) уравнения, удовлетворяющее условию у = у0 при х = х0, называемых начальными. Определение: Общим решением уравнения (2) в некоторой области G, называется функция у = φ (х, С), где С произвольная постоянная, если она является решением уравнения (2) при любом значении постоянной С и если при любых начальных условиях, таких что что (х0, у0) ∈ G существует единственное значение постоянной С = С0 , такое что функция у = φ (х, С0) удовлетворяет начальным условиям: φ (х0, С0) = у0. Определение: Частным решением уравнения (2) в некоторой обл. G, называется функция у = φ (х, С0), которая получается из общего решения у = φ (х, С) при определенном значении постоянной С = С0 . Пример: Рассмотрим уравнение у’= 3х2 , удовлетворяющее всем условиям теоремы Коши. Функция у = х3 + С, где С – произвольная постоянная является общим решением данного уравнения во всей плоскости Оху. Уравнения с разделяющимися переменными. Определение: Уравнение вида у’ = f1 (x) и f2 (у) (3), где f1 (x) и f2 (у) - непрерывные функции, называется дифференциальным уравнением с разделяющимися переменными. Для отыскания решения уравнение (3) нужно разделить в нем переменные, т.е. перепишем (3) в виде:  = = f1 (x) ∙ f2 (у). Разделим на f2 (у) и умножим на = = f1 (x) ∙ f2 (у). Разделим на f2 (у) и умножим на 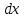 последнее уравнение. Получим: последнее уравнение. Получим: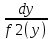 = f1 (x) = f1 (x)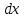 отсюда интегрированием получим выражение отсюда интегрированием получим выражение = =  + С, где С = const, которое называется общим решением уравнения (3). + С, где С = const, которое называется общим решением уравнения (3).Пример: Решить уравнение у’=  . Здесь f1 (x) = . Здесь f1 (x) = 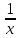 , f2 (у) = у , f2 (у) = у = =  , ,  = = 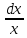 ⟹ ⟹  = =  + С, С ≠ 0 + С, С ≠ 0или  потенцируя находим потенцируя находим  , или у = ± , или у = ±  , , если ± 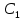 = С, то у = Сх – общее решение этого уравнения. = С, то у = Сх – общее решение этого уравнения.Пусть требуется выделить из общего решения частное, удовлетворяющее начальным условиям х0 =1, у0 =2. Подставляя эти значения в общее решение, получили: 2 = С ∙ 1 ⟹ С = 2 т.о. искомое частное решение у = 2х Линейные уравнения. Определение: Уравнение вида (4) у’ + p(х) у = f(x), где р(х) и f(x) – непрерывные функции, называется линейным дифф – ым уравнением 1-го порядка. Если f(x) = 0, то уравнение (4) называется линейным однородным уравнением. Если f(x) ≠ 0, то ур-ние (4) называется линейным неоднородным уравнением. Для нахождения общего решения ур-ния (4) применяется метод вариации постоянной. Сначала находим общее решение линейного однородного уравнения у’ + p(х) у = 0, которое является уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, получили:  = - р(х) = - р(х)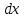 , ,  = - = -  + +  Отсюда потенцируя, получили: У = ±  или у = или у =  , (*) где С = const. , (*) где С = const.Теперь получим общее решение линейного неоднородного уравнения. Будем искать его в виде (*), где С будем считать непостоянной а функцией от х, т.е. у =  (*’) (*’)Чтобы найти С(х) подставим (*’) в (4), получим:  - C(х) р(х) - C(х) р(х) + р(х)С(х) + р(х)С(х) = f(x) = f(x) = f(x) = f(x) Чтобы (*’) было решением (4) нужно чтобы С(х) удовлетворяло последнему рав-ву. Интегрируя его, получим: С(х) =  + С1 , где С1, = const. + С1 , где С1, = const.Подставляя С(х) в (*’), получим общее решение уравнения (4). у(х) =  + +   Пример: Найти общее решение уравнения у’ + 3у = е2х Решаем сначала соответствующее однородное уравнение. у’ + 3у = 0  = -3у, = -3у,  = - 3dx, = - 3dx,  = - = -  = - 3х + = - 3х +  ⟹ у = ±С1е- 3х общее решение однородного уравнения. ⟹ у = ±С1е- 3х общее решение однородного уравнения.Ищем общее решение неоднородного уравнения в виде у = С(х) е- 3х у’ = С’(х) е- 3х - 3С(х) е- 3х Подставляем в исходное уравнение выражения для у и у’. С’(х) е- 3х - 3С(х) е- 3х + 3С(х) е- 3х = е2х С’(х) е- 3х = е2х С’(х) = е5х или dС = е5х dx ⟹ С(х) =  е5х + С2 , где С2 = const. е5х + С2 , где С2 = const.Т.о. общее решение исходного уравнения имеет вид: У = С(х) е- 3х = (  е5х + С2) е-3х ⟹ у = = е5х + С2) е-3х ⟹ у = =  е2х + С2 е- 3х е2х + С2 е- 3х Дифференциальные уравнения второго порядка. Определение: Уравнение вида F(x, y, y’, y”) = 0, где х – независимая переменная, у – искомая функция, y’ и y” – ее производные, называется дифференциальным уравнением 2-го порядка. Обычно изучают уравнение, которое могут быть записаны в виде: Y” = f(x, y, y’) (1) Уравнения второго порядка, допускающие понижение порядка. Отметим три частных вида уравнения (1), когда решение его с помощью замены переменной сводится к решению уравнения первого порядка. Такое преобразование урав-ия (1) называется понижением порядка. 1). Уравнение вида y” = f(x). Уравнение не содержит у и y’. Введем функцию z(x), положив z(x) = y’. Тогда z’(x) = y” и уравнение превращается в уравнение первого порядка: z’(x) = f(x) с искомой функцией z(x). Решая его, находим z(x) = |
