Математика лекции. Лекции. Тема Дифференциальное интегральное исчисление
 Скачать 184.94 Kb. Скачать 184.94 Kb.
|
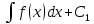 или у’ = или у’ = 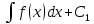 ⟹ получим искомое решение: ⟹ получим искомое решение:у = 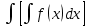 dx + C1 х + С2, где С1, С2 - произвольные постоянные. dx + C1 х + С2, где С1, С2 - произвольные постоянные.Пример 1. Найти общее решение уравнения y”= х Положим y’ y’ , тогда z’(x) = х. Интегрируя, находим: z(x) = 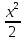 + С1 ⟹ y’ = + С1 ⟹ y’ = 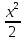 + С1 интегрируем еще раз: + С1 интегрируем еще раз: у = 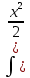 + С1) + С1) 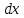 + С2 = + С2 = 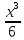 + С1 х + С2 + С1 х + С22). Уравнение вида y” = f(x, у’). Уравнение не содержит у. Положим z(x) = y’, тогда z’(x) = y” и уравнение преобразуется в уравнение первого порядка: z’ = f(x, z). Решив его, находим z(x) = φ (х, С1) или y’ = φ (х, С1). Отсюда интегрируя, получим у = 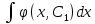 + С2 , где z, С2 - const. + С2 , где z, С2 - const.Пример 2. Найти общее решение уравнения z - 3 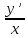 = х. = х.Положим z(x) = y’ и z’(x) = y”, получим линейное уравнение первого порядка: z’ - 3 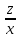 = х Решаем его: z’ - = х Решаем его: z’ - 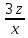 = 0 , = 0 , 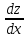 = = 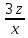 , , 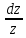 = 3 = 3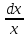 ⟹ ⟹ 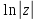 = 3 = 3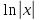 + + 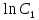 , z = , z = 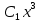 . Тогда . Тогда z(x) = + С1 (х) х3 . Находим z’ = С’1 (х) х3 + 3 С1 (х) х2 , подставим z и z’ в исходное уравнение: С’1 (х) х3 + 3 С1 (х) х2 - 3 С1 (х) х2 = х, С’1 (х) х3 = х, С’1 (х) = 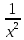 , ,С1 (х) = - 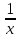 т.о. z(x) = - х2 или z = С1 х3 - х2 или y’= С1 х3 - х2 ⟹ у = С1 т.о. z(x) = - х2 или z = С1 х3 - х2 или y’= С1 х3 - х2 ⟹ у = С1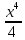 - - 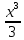 + С2. + С2.3). Уравнение вида y”= f(y, y’). Уравнение не содержит х. В этом случае вводим функцию z(у), полагая y’ = z. Тогда y” = 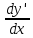 = = 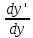 ∙ ∙ 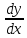 = = 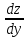 ∙ ∙ 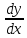 = = 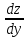 z(y). z(y).Подставим в уравнение выражения y’ и y”, получим уравнение 1-го порядка относительно z, как функции от у. z = 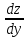 = f(у, z). = f(у, z).Решив его, находим: z = φ (у, С1) или 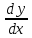 = φ (у, С1) ⟹ = φ (у, С1) ⟹ 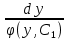 = dx - уравнение с разделяющимися переменными. Тогда решив его, получим: = dx - уравнение с разделяющимися переменными. Тогда решив его, получим: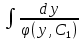 = = 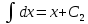 , где , где С1, С2 - const. Пример 3. Найти общее решение уравнения yy” – 2y’2 = 0 Положим y’ = 2(y) y” = z 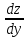 получим: получим:zy 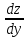 - 2z2 = 0, y - 2z2 = 0, y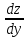 - 2z = 0, y - 2z = 0, y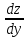 = 2z, = 2z,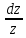 = = 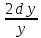 ⟹ ⟹ 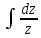 = 2 = 2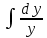 , , 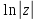 = = 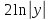 + + 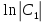 , т. е. z = C1y2 т.к. z = , т. е. z = C1y2 т.к. z = 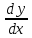 , получим , получим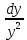 = С1dx ⟹ - = С1dx ⟹ - 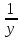 = C1x + C2 или у = - = C1x + C2 или у = - 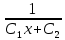 искомое решение. искомое решение.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Определение: Уравнение вида y” + p(x) y’ + q(x) y = f(x), где у – искомая функция, а р(х), q(x) и f(x) непрерывные функции на некотором интервале (а,b), называется линейным дифференциальным уравнением второго порядка. Если f(x) = 0, то данное уравнение называется однородным линейным уравнением, если f(x) ≠ 0 - неоднородным линейным уравнением. Рассмотрим линейное однородное уравнение второго порядка (1) y” + py’ + qy = 0, где р и q – вещественные числа. Теорема 1: Если число k является корнем уравнения k2 +pk + q = 0 (2), то функция у = ekx является решением уравнения (1). Док-во: Пусть у = ekx k = const. Тогда y’ = ekx ekx , y” = k2 ekx . Подставляя у, y’ и y” в уравнение (1), получим ekx(k2+ pk + q)= 0 т.к. ekx≠ 0, то сокращая на ekx , получим уравнение k2 +pk + q = 0 Следовательно, функция у = ekx является решением уравнения (1). Уравнение (2) называется характеристическим урав-ем ур-ия (1). Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через k1 и k2. Теорема 2: Общее решение уравнения (1) может быть записано следующим образом: 1) если корни характеристического уравнения вещественные и равные (k1 = k2), то общее решение имеет вид: у = С1 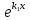 + С2 + С2 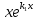 ; ;2) если корни характеристического уравнения вещественные и различные (k1 ≠ k2), то общее решение имеет вид: у = С1 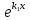 + С2 + С2 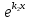 ; ;3) если корни характеристического уравнения комплексные (k1 = α + ιβ, k2 = α – ιβ, β ≠ 0), то общее решение имеет вид: у = 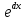 (C1 (C1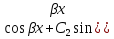 . .Пример 1: Найти общее решение уравнения: y” + y’ – 2y = 0 Характер-ое ур-ие имеет вид k2 + k – 2 = 0, его корни k1 = 0, k2 = - 2 - вещественные и различные. Соответствующие частные решения уравнения: у1 = С1ех, у2 = С2 е- 2х. Общее решение ур-ния имеет вид: у = С1ех + С2 е- 2х Пример 2. Найти общее решение уравнения y” - 2y’ + y = 0 Характ-ое ур-ие: k2 - 2k + 1 = 0, его корни k1 = k2 = 1 – вещественные и равные. Соответствующие частные решения y1 = ех, у2 = хех . Общее решение уравнения имеет вид: у = С1ех + С2 хех Пример 3. Найти общее решение уравнения y” - 4y’ + 13y = 0 Характ-ое урав-ие: k2 - 4k + 13 = 0, его корни k1 =2 + ι3, k2 = 2 - ι3 - комплексные. Соответствующие частные решения: у1 = е2х 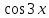 , у2= е2х , у2= е2х 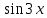 . Общее решение уравнения имеет вид: . Общее решение уравнения имеет вид: у = е2х 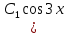 + + 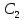 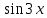 ) )Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Рассмотрим линейное неоднородное уравнение второго порядка: (3) y” + py’ +y = f(x), где p и q – вещественные числа, f(x) – непрерывная функция. Рассмотрим различные виды правых частей уравнения (3). 1). Пусть правая часть имеет вид f(x) = Pn(x) где Pn(x) = a0xn + a1xn-1 +. . . + an1x + an – многочлен степени n. Тогда частное решение можно искать в виде: 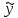 = Qn (x)xr , где = Qn (x)xr , где Qn (x) – многочлен той же степени что и Pn(x), а r число корней характ-го ур-ния, равных нулю. Пример 4. Найти общее решение уравнения y” - 2y’ + y = х + 1 Общее решение соотв –го однородного ур-ния имеет вид : У = (С1 + С2 х) ех , (см. пример 2). Т.к. правая часть уравнения многочлен первой степени и ни один из корней характеристического урав-ия k2 - 2k + 1 = 0 не равен 0, то частное решение ищем в виде: 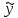 = (Ax + B)x0 = Ax +B, где A и B неизвестные коэффициенты. = (Ax + B)x0 = Ax +B, где A и B неизвестные коэффициенты.Дифференцируя дважды 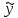 и подставляя и подставляя 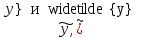 в данное уравнение, находим: в данное уравнение, находим:- 2 A + Ax + B = x + 1 ⟹ A = 1, - 2A + B = 1⟹ A = 1, B = 3. Частное решение уравнения имеет вид: 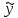 = х + 3, а его общее решение - = х + 3, а его общее решение - у = У + 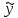 = (С1 + С2х) ех + х + 3. = (С1 + С2х) ех + х + 3.2). Пусть правая часть имеет вид: f(x) = е2х Pn(x), где Pn(x) – многочлен степени n. Тогда частное решение следует искать в виде 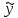 = Qn (x)xrеα х, = Qn (x)xrеα х,где Qn (x) – многочлен той же степени, что и Pn(x), а r, число, показывающее сколько раз α является корнем характ-го уравнения. Пример 5. Найти общее решение уравнения y” - 4y’ + 3y = х ех Здесь характ-ое уравнение k2 - 4k + 3 = 0 имеет корни k1 = 1, k2 = 3. Значит общее решение соотв-го однородного уравнения имеет вид: У = С1ех + С2е3х В правой части данного уравнения стоит произведение многочлена 1-ой степени на показательную функцию еα х при α = 1 т.к. среди корней характ-го уравнения только один корень k1 = α = 1, то r = 1. Поэтому частное решение данного уравнения ищем в виде 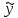 = (Ах + В) хех = (Ах2 + Вх) ех = (Ах + В) хех = (Ах2 + Вх) ех Дифференцируя и подставляя в уравнение, получаем: - 4Ах + 2А – 2В = х ⟹ - 4А = 1, 2А – 2В = 0 ⟹ А = - 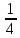 , В = - , В = - 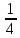 Тогда частное решение данного уравнения 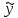 = - = - 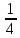 (х2 + х) ех , а общее решение - (х2 + х) ех , а общее решение -у = С1ех + С2е3х - 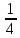 (х2 + х) ех. (х2 + х) ех.3). Пусть правая часть имеет вид f(x) = a 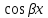 + b + b 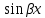 , где а, , где а, 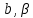 - известные числа. Тогда частное решение надо искать в виде - известные числа. Тогда частное решение надо искать в виде 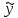 = ( А = ( А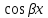 + В + В 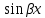 ) хr , где А и В - неизвестные коэффициенты, а r – число, равное числу корней характеристического уравнения совпадающих с i β. ) хr , где А и В - неизвестные коэффициенты, а r – число, равное числу корней характеристического уравнения совпадающих с i β.Пример 6. Найти общее решение уравнения y” + у = 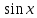 . .Здесь характ-ое ур-ние k2 + 1 = 0 имеет корни k1 = i, k2 = - i. Поэтому общее решение соотв-го однородного уравнения будет У = С1 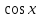 + С2 + С2 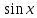 . В правой части стоит функция . В правой части стоит функция 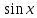 , т.е. а = 0, , т.е. а = 0, 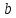 = 1, = 1, 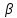 = 1. = 1. Т.к. i β = i является корнем характ-го уравнения, то r = 1 и частное решение ищем в виде 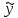 = (А = (А 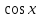 + В + В 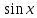 ) ) 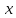 Дифференцируя и подставляя в уравнение , получим: 2 (- А 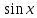 + В + В 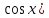 = = 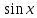 ⟹ А = - ⟹ А = - 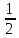 , В = 0 т.о. частное решение , В = 0 т.о. частное решение 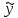 = - = - 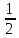 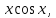 а общее решение у = 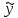 + У = С1 + У = С1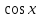 + С2 + С2 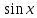 - - 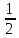 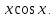 4). Пусть правая часть имеет вид f(x) = еα х 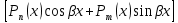 , ,где 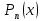 - многочлен степени n, а - многочлен степени n, а 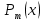 - многочлен степени m. Тогда частное решение следует искать в виде: - многочлен степени m. Тогда частное решение следует искать в виде: 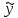 = хr еα х = хr еα х 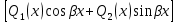 , ,где 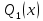 и и 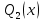 - многочлены степени S, S = max - многочлены степени S, S = max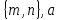 r – число равное числу корней характ-го ур-ния совпадающие с α + i β. r – число равное числу корней характ-го ур-ния совпадающие с α + i β.Пример 7. Найти общее решение уравнения у”- y = 3eα x |
