статистика. Задача Статистическая сводка и группировка. Теория по решению задачи
 Скачать 364.3 Kb. Скачать 364.3 Kb.
|
|
Примеры решения задач по статистике Задача Статистическая сводка и группировка. Теория по решению задачи. Статистическая сводка – научно обработанный материал статистического наблюдения в целях получения обобщенной характеристики изучаемого явления. Группировка – распределение единиц изучаемого объекта на однородные типичные группы по существенным для них признакам. Интервал – разница между максимальным и минимальным значением признака в каждой группе. i – величина интервала; R – размах колебания (R=xmax-xmin)  РЕКЛАМА n – принятое число групп; xmax, xmin – наибольшее и наименьшее значение признака в изучаемой совокупности. N – число наблюдений Типовая задача № 1 Распределите потребительские общества по размеру товарооборота на 3 группы с равными интервалами. В каждой группе подсчитайте количество потребительских обществ, сумму товарооборота, сумму издержек обращения. Результаты группировок представьте в табличной форме. К какому виду статистических таблиц относится составление вами таблица, и какой вид группировки она содержит? Имеются основные экономические показатели потребительских обществ за отчетный период: Таблица № 1
Ход решения задачи: Т. к. нам известен группировочный признак, работу необходимо начать в определения величины интервала по формуле: Образец 3 группы потребительских обществ по размеру товарооборота. Определяем границы групп: 1 группа: 180+90=270 (180-270) 2 группа: 270+90=360 (270-360) 3 группа: 360+90+450 (360-450) После того, как выбран группировочный признак, намечено число групп и образованы сами группы, необходимо отобрать показатели, которыми будут характеризоваться группы, и определить их величину по каждой группе. В нашем примере каждую группу необходимо охарактеризовать следующими показателями: а) количеством потребительских обществ; б) суммой товарооборота; в) суммой издержек обращения. Для заполнения итоговой таблицы составим предварительно рабочие таблицы № 2, 3, 4. Группа потребительских обществ с товарооборотом от 180 до 270 млн. грн. Таблица № 2
Группа потребительских обществ с товарооборотом от 270 до 3660 млн. грн. Таблица № 3
Группа потребительских обществ с товарооборотом от 360 до 450 млн. грн. Таблица № 4
Итоговые показатели рабочих таблиц занесем в окончательную итоговую таблицу и получим групповую таблицу № 5. Группировка потребительских обществ, по размеру товарооборота: Таблица № 5
Вывод: По результатам итоговой таблицы можно сделать вывод, что с увеличением объема товарооборота потребительских обществ, относительный показатель уровня издержек обращения снижается. Следовательно, между ними существует обратная связь. Составленная нами таблица является групповой таблицей, т. к. ее подлежащее содержит группы потребительских обществ по размеру товарооборота. Она содержит аналитический вид группировки. Задача - Ряды распределения и статистические таблицы. Теория по решению задачи. Статистический ряд распределения – упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку. Дискретный вариационный ряд – характеризует распределение единиц совокупности по дискретному (прерывному) признаку. Интервальный вариационный ряд – характеризует распределение единиц совокупности по интервальному (непрерывному) признаку. Для изображения дискретных вариационных рядов распределения используется «полигон распределения». Для графического изображения интервального вариационного ряда применяются «гистограмма» и «кумулята». Задача 1. На экзамене по истории студенты получили оценки: 3 4 4 4 3 4 3 4 3 5 4 4 5 5 2 3 2 3 3 4 4 5 3 3 5 4 5 4 4 4 Построить дискретный вариационный ряд распределения студентов по баллам и изобразить его графически. Ход решения задачи: Определяем элементы ряда распределения: варианты, частоты, частоты.
Теперь графически изобразим дискретный ряд распределения в виде помпона распределения. 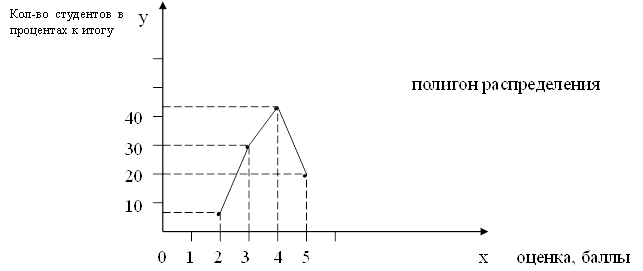 Можно сделать вывод о том, что преобладающее большинство студентов получило «4» (43,3 %). Задача 2. Во время выборочной проверки было установлено, что продолжительность одной покупки в кондитерском отделе магазина была такой: (секунды). 77 70 82 81 81 82 75 80 71 80 81 89 75 67 78 73 76 78 73 76 82 69 61 66 84 72 74 82 82 76 Построить интервальный вариационный ряд распределения покупок по продолжительности, создав 4 группы с одинаковыми интервалами. Обозначить элементы ряда. Изобразить его графически, сделать вывод. Ход решения задачи по статистике: Определяем элементы ряда распределения: варианты, частоты, частости, накопленные частоты. Но прежде рассчитаем границы 4 заданных групп с одинаковыми интервалами: Величину интервала определим по формуле В нашем случае Границы групп соответственно равны: I 61+7=68 (61-68) II 68+7=75 (68-75) III 75+7=82 (75-82) IV 82+7=89 (82-89)
Теперь графически отобразим наш интервальный вариационный ряд в виде гистограммы и кумуляты. 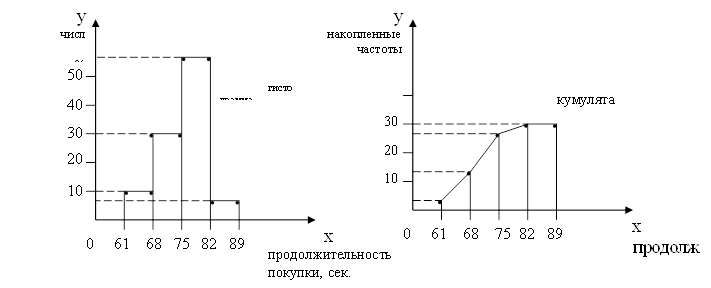 По таблице и графика можно сделать вывод о том, что преобладающее большинство покупок (16 или 53.3%) находится во временном интервале 75-82, сек. Статистика задача - Абсолютные и относительные величины. Теория по решению статистической задачи. Абсолютные величины – показатели, которые выражают размеры общественных явлений и процессов числом единиц совокупности. Относительные величины – показатели, выражающие количественные соотношения численностей или величин признаков изучаемых явлений. Виды относительных величин: 1) Относительная величина выполнения плана: 2) Относительная величина планового задания: 3) Относительная величина динамики: 4) Относительная величина структуры: 5) Относительная величина сравнения отражает соотношение двух объемов или уровней в пространстве: соотношение производства автомобилей в Украине и России, соотношение уровней оплаты труда в разных хозяйствах, соотношение уровней производительности на разных предприятиях отрасли и т. д. 6) Относительная величина координации получается посредством деления друг на друга разноименных исходных показателей, она дает типичную характеристику соотношения одно-порядковых по значимости исходных показателей, во-первых, непосредственно связанных между собой, во-вторых, обладающих некоторой общностью. 7) Относительная величина интенсивности: 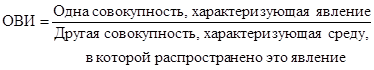 Типовая задача № 1 Два консервных завода выработали по 100 тыс. шт. банок виноградного сока. На первом заводе емкость каждой банки составляет 500 см3, а на втором – 200 см3. Можно ли сказать, что оба завода работали одинаково? Ход решения задачи по статистике: Для того, чтобы ответить на этот вопрос необходимо установить коэффициенты перевода фактического объема банок в условные банки и затем умножить количество выпущенных банок на эти коэффициенты. Представим расчет в таблице № 1. Таблица № 1
Таким образом, завод № 1 по сравнению с заводом № 2 выпустил виноградного сока на 84,8 тыс. Банок больше (141,4-56,6). Статистика - Типовая задача № 2 Имеются следующие данные розничного товарооборота: Таблица № 2
Определить: 1. Относительную величину выполнения плана. 2. Относительную величину планового задания. 3. Относительную величину динамики. Ход решения задачи: 1. Определяем относительную величину выполнения плана по двум универмагам: 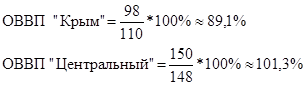 2. Определим относительную величину планового задания: 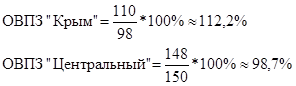 3. Определяем относительную величину динамики: 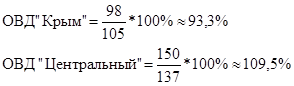 Статистическая задача - Средние и структурные средние величины. Теория по решению статистической задачи: Средние величины – это показатели. Выражающие типичные черты и дают обобщающую количественную характеристику уровня признака по совокупности однородных явлений. 1. Средняя арифметическая: 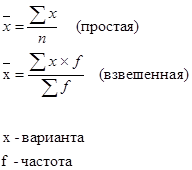 2. Средняя гармоническая: 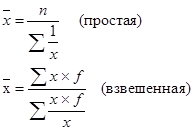 3. Средняя квадратическая: 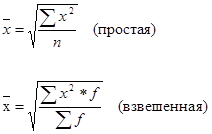 4. Средняя хронологическая: 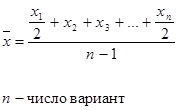 5. Средняя геометрическая: 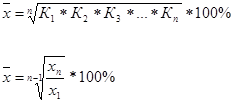 К1, К2, К3 и Кn – коэффициенты динамики по отношению к предыдущему периоду. 6. мода интервальных рядов распределения вычисляется по следующей формуле: х0 – минимальная граница модального интервала; i – величина интервала; f2 – частота модального интервала; f1 – частота интервала, предшествующего модальному; f3 – частота интервала, следующего за модальным. Мода для дискретных рядов распределения – это наиболее часто встречающаяся величина признака в данной совокупности. 7. Медиана для интервальных рядов распределения вычисляется по формуле: 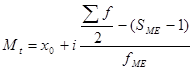 x0 – нижняя граница медианного интервала; i – величина медианного интервала; ∑f – сумма частот ряда; SМЕ-1 – сумма накопленных частот, предшествующих медианному интервалу; fМЕ – частота медианного интервала. Чтобы определить медиану в дискретном вариационном ряду. Необходимо сумму частот разделить пополам и к полученному результату добавить ½. Типовая задача № 1 Имеются следующие данные о заработной плате рабочих: Таблица № 1
Определите среднюю заработную плату одного рабочего. Ход решения: Среднюю заработную плату определим по формуле средней арифметической взвешенной: Т. о. средняя заработная плата рабочего составила 205,27 грн. Типовая задача (статистика) № 2 Имеются, следующие данные выпуска литья в литейном цехе завода за пятилетний период: Таблица № 2
Требуется определить средний темп выпуска литья. Ход решения задачи: Для определения среднего темпа выпуска литья используем формулу средней геометрической: 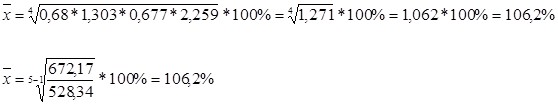 Типовая задача № 3 Имеются следующие данные: Таблица № 3
Определить моду и медиану. Ход решения задачи: 1. Определяем моду: 2. Определяем медиану: Практические задачи по статистике для самостоятельного решения с ответами Задача по статистике 1. Имеются следующие данные об урожайности зерновых культур:
Определить среднюю урожайность зерновых культур, моду и медиану. Ответ._К_использования_среднесписочной_численности_0,96_%Коэффициент_использования_среднеявочной_численности_0,99_%Задача_8.'>Ответ._Сумма_ежегодных_отчислений_16,6_тыс._грн.Общая_норма_амортизации_6,6_%.Задача_по_статистике_6.'>Ответ._Средний_вес_детали_колеблется_в_пределах_29,44_‹_х_‹_30,56.Задача_4.'>Ответ._средняя_урожайность:_30,3_ц/гамода:_33,3медиана:_30,8Задача_2.'>Ответ. средняя урожайность: 30,3 ц/га мода: 33,3 медиана: 30,8 Задача 2.
Требуется определить: (цепным и базисным способом): 1) абсолютный прирост; 2) темп роста и прироста; 3) средний абсолютный прирост; 4) средние темпы роста и прироста. Ответ 2. цепным способом базисным способом абсолютный прирост 18 абсолютный прирост 18 11 29 7 36 5 41 темп роста 1,12 темп роста 1,12 1,07 1,19 1,04 1,24 1,03 1,27 темп прироста 0,12 темп прироста 0,12 0,07 0,19 0,04 0,24 0,03 0,27 средний абсолютный прирост: 31 средний абсолютный прирост: 31 средний темп роста 1,02 средний темп роста: 1,05 средний темп прироста 0,02 средний темп прироста: 0,05 Задача 3. Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате проверки был установлен средний вес детали 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,954 требуется определить предел в котором находится средний вес деталей в генеральной совокупности. Ответ. Средний вес детали колеблется в пределах 29,44 ‹ х ‹ 30,56. Задача 4. По имеющимся данным определить индивидуальные и общий индексы себестоимости и экономию (перерасход) от снижения (роста) себестоимости.
Ответ. Индивидуальный индекс себестоимости по электробритве 0,985 Индивидуальный индекс себестоимости электрофену 1,02 Общий индекс себестоимости 0,99. Перерасход денежных средств от роста себестоимости 144 грн. Задача 5. Полная первоначальная стоимость оборудования 250,4 тыс. грн. Это оборудование может работать 20 лет при условии проведения в капитальных ремонтов на сумму 2,5 тыс. грн. каждый. После полного износа оборудования может быть реализовано как металлолом за 1 тыс. грн. Затраты на модернизацию в течении срока службы 62,6 тыс. грн. Определить сумму ежегодных амортизационных отчислений, общую норму амортизации. Ответ. Сумма ежегодных отчислений 16,6 тыс. грн. Общая норма амортизации 6,6 %. Задача по статистике 6. Определить календарный, режимный, располагаемый (плановый) и фактический фонды станочного времени по 2 видам станков и коэффициенты использования станочного времени за апрель по таким данным:
Число рабочих дней в апреле 22. Режим работы – 2 смены. Установленная продолжительность смены: 8 часов. Ответ. Календарный фонд 72000 станкочасов Режимный фонд 35200 станкочасов Плановый фонд 35060 станкочасов Фактический фонд 31547 станкочасов Коэффициент использования календарного фонда 43,8 % Коэффициент использования режимного фонда 89,6 % Коэффициент использования планового фонда 90 % Задача 7. В квартале 62 рабочих дня, отработало 136400 человеко-дней; целодневные простои 930 человеко-дней; неявок по различным причинам (включая праздничные и выходные) 69670 человеко-дней. Определить: коэффициенты использования среднесписочной и среднеявочной численности. Ответ. К использования среднесписочной численности 0,96 % Коэффициент использования среднеявочной численности 0,99 % Задача 8. На заводе с численностью персонала 3000 человек производительность труда выросла на 25 %, а на заводе, где работают 5000 человек, снизилась на 5 %. Как изменилась производительность труда на 2-х заводах вместе. Ответ. Увеличилась на 6 % производительность на двух заводах. Задача 9 по статистике Объем продукции в натуральном выражении на предприятии вырос за отчетный период на 28 %, а производственные затраты в целом возросли на 19 %. Определить как изменилась себестоимость единицы продукции. К задаче 9 ответ Себестоимость единицы продукции снизилась на 7 %. Задача 10. Какой была численность населения в начале и конце года, если среднегодовой показатель ее за этот год составил 800 тыс. человек, сальдо миграции + 32 тысячи человек, коэффициент естественного прироста 30 % 0. Ответ - Численность на начало года 772000 человек. К задаче 10. Численность на конец года 828000 человек. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
