работа стат. Задача Статистический анализ одномерной последовательности случайных величин
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
Заключение________________________________________________________ Часть 2 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
В качестве целевой функции (функции отклика, зависимой переменной, реакции системы на воздействие факторов Xi) Y принята Re=X1*X2/X3, (единица безразмерная): 2. Реалистичное содержание (сущность) факторов В качестве факторов функции отклика Xi принимаются: X1 - скорость движения жидкости, м/с; X2 -характерный размер (для трубопровода- внутренний диаметр трубы, м); Х3 - кинематическая вязкость жидкости, м2/с. 3. Уровни варьирования значений факторов Минимальные и максимальные значения факторов приняты следующие:
4. Среднее значение фактора Среднее значение фактора определяется по формуле: X10 = 0,10+014/2=0,12; X20 = 0,1+0,15/2= 0,125; X30 = 0,000025+0,000035/2= 0,00003. 5. Интервалы варьирования фактора Интервал варьирования определяется по формуле: dx1 = X10 – X1min = 0,12-0,1= 0,02. dx2 = X20 – X2min = 0,125-0,1= 0,025. dx3 = X30 – X3min = 0,00003-0,000025= 0,000005. 6. Корректность определения значений факторов
7. Нормированные значения факторов Нормированные значения определяются формулой:  . .Хн1 = 0,14-0,12/0,02=1 ; Хн2 = 0,15-0,125/0,025=1; Хн3= 0,000035-0,00003/0,000005=1. 8. Матрица планирования полного факторного эксперимента Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен и равен 1.
9. Экспериментальные значения целевой функции
Расчет среднего арифметического результатов каждого опыта
9. Дисперсия среднего арифметического для каждой строки матрицы эксперимента (каждого опыта) Дисперсия среднего арифметического определяется формулой: где ?????.
12. Оценка однородности построчных дисперсий Расчетное значение критерия Кохрена. Критерий Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них, и определяется по формуле:  где ?????. Максимальное значение дисперсии результатов опыта: S2ymax= 37,3. Сумма всех построчных дисперсий: 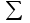 S2 y = 16,3+37,3+37,3+22+13,7+22+14,2+14,5=177,3. S2 y = 16,3+37,3+37,3+22+13,7+22+14,2+14,5=177,3.Расчетное значение критерия Кохрена: Gp= 37,3/177,3=0,21. В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N , где N – число опытов (количество строк в матрице планирования). Табличное значение критерия Кохрена. Уровень значимости. = 0,05. Степень числителя (f1): f1= m –1= 5-1= 4, где m – количество параллельных опытов в строке матриц Степень свободы знаменателя (f2): f2 = N = 8, где N – общее число опытов в матрице. Табличное значение критерия Кохрена Gт = 0,3910. Вывод: Следовательно, с достоверностью 1 – , т.е. 0,05 все построчные дисперсии являются однородными 13. Вид уравнения регрессии, принятого для построения модели функции отклика Рекомендуется полиномиальная модель функции отклика y = b0X0+b1X1+b2X2+b3X3+b12X1X2+b13X1X3+b23X2X3+b123X1X2X3 14. Коэффициенты регрессии Значения коэффициентов регрессии определяются по формулам:  ; ; и так далее для всех коэффициентов. Таблица - Значения коэффициентов регрессии.
15. Статистическая значимость коэффициентов регрессии Расчетные значения критерия Стьюдента. Оценка производится по t-критерию Стьюдента. Проверяется отклонение от нуля найденной оценки. Для каждого коэффициента bk вычисляется расчетное значение критерия Стьюдента:  ; ;; где bk – коэффициент уравнения регрессии; S{bk} – оценку дисперсию коэффициентов, найденных по экспериментальным данным; - дисперсия коэффициентов, найденных по экспериментальным данным; S2b = 16,3+37,3+37,3+22+13,7+22+14,2+14,5/8 = 22,16. S2{bk} = 22,16/8*5= 0,554. S{bk} = 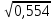 =0,744. =0,744.Расчетные значения критерия Стьюдента
Табличные значения критерия Стьюдента. Уровень статистической значимости. = 0,05. Степень свободы f = 8*(5-1)= 32. 16 Функция отклика со статистически значимыми коэффициентами. Функция отклика со статистически значимыми коэффициентами имеет вид: y = b0X0+b1X1+b2X2+b3X3+b12X1X2+b23X2X3+b13X1X3+b123X1X2X3 17 Значения функции отклика для каждого опыта по новой функции отклика со статистически значимыми коэффициентами
21 Проверка адекватности новой функции отклика со статистически значимыми коэффициентами Расчетное значение критерия Фишера (F- критерия). Адекватность модели проверяют по критерию Фишера , расчетное значение которого определяется по формуле: Fp= S2ад/S2в ; ; , где ???? S2ад = 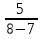 ((403,6-404)2+(423,6-419)2+(468,6-474,6)2+(503-502,6)2+(519,8-520,2)2+(547-542,2)2+(580,8-585,4)2+(596-595,6)2)= 510; ((403,6-404)2+(423,6-419)2+(468,6-474,6)2+(503-502,6)2+(519,8-520,2)2+(547-542,2)2+(580,8-585,4)2+(596-595,6)2)= 510;S2в = (16,3+37,3+37,3+22+13,7+22+14,2+14,5)/8 = 22,16; Fp = 510/22,16= 23,014. Уровень значимости = 0,05. Степень свободы адекватности: fад = 8-7= 1. Степень свободы воспроизводимости: fв = 8(5-1) = 32. Табличное значение критерия Фишера. Fт = 4,2. 22 Функция отклика со статистически значимыми коэффициентами и натуральными факторами Функция отклика со статистически значимыми коэффициентами и натуральными факторами имеет вид: y = b0 + b1 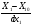 + b2 + b2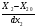 + b3 + b12 + b3 + b12 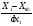 + b13 + b13 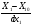 + b23 + b123 + b23 + b123 Заключение _________________________________________________________ Литература
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
