работа стат. Задача Статистический анализ одномерной последовательности случайных величин
 Скачать 0.67 Mb.
|
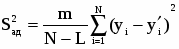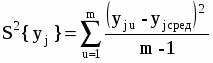          Часть 1 СТАТИСТИЧЕСКИЙ АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИНЗадача 1. Статистический анализ одномерной последовательности случайных величин Цель работы: приобрести компетенции статистического анализа одномерной последовательности случайных величин. Задание:
В качестве исходных данных принята [числовые характеристики из нефтегазовой сферы] (табл. 1). Таблицы 1- Наименование случайной величины, е.и.
Вариационный ряд – упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины. Для заданной последовательности случайных величин вариационный ряд показан в (таблица 2). Таблица 2- Вариационный ряд для _____________________________
Характеристиками вариационного ряда:
Статистический ряд – это упорядоченный ряд распределения единиц совокупности на группы по определенному варьирующему признаку. Он характеризует состав изучаемого явления, позволяет судить об однородности совокупности, границах ее изменения, закономерностях развития наблюдаемого объекта. Для заданной последовательности случайных величин вариационный ряд показан в таблице 3.
Группированный статистический ряд - совокупность промежутков и соответствующих им частот (абсолютных и относительных) называют группированным статистическим рядом. Таблица 3- Статистический ряд случайных величин, k
4.Интервальный ряд Группированный ряд – это упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений величины. Для построения группированного ряда примем t = 10 интервалов. Ширина интервалов оправляются по формуле: rt = R/t + Δt, где - R – размах вариационного ряда; t – количество интервалов; Δ – малая величина, позволяющая исключить повтор границ интервалов (рекомендуется назначить равной 0,1% от размаха интервала). rt = 9,874. Таблица 4 – Значения границ интервалов
Интервальный ряд представлен в таблице 5. Таблица 5 - Интервальный ряд
Гистограмма - способ графического представления табличных данных. Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра. . Гистограмма по значениям группированного ряда показана на рис. 1. Рисунок 1 - Гистограмма для группированного ряда Гистограмма по средним значениям интервального ряда показана на рис. 2. Рисунок 2 - Гистограмма для интервального ряда
Полигон – один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов. Полигон для группированного ряда показан на рисунке 3. Рисунок 3 – Полигон Полигон для интервального ряда показан на рис. 4 Рисунок 4 – Полигон для интервального ряда
Кумулята –это изображение распределения в виде кривой, ординаты которой пропорциональны накопленным частотам вариационного ряда. Кумулята для группированного показан на рисунке 5. Рисунок 5 – Кумулята для группированного ряда Кумулята для интервального ряда показан на рисунке 6. Рисунок 6 – Кумулята для интервального ряда
Огива строится аналогично кумуляте, с той лишь разницей, что на ось абцисс наносят накопления частоты, а на ось ординат – значение признака. Огива для группированного ряда показана на рисунке 7. Рисунок 7 – Огива для группированного ряда Огива для интервального ряда показана на рисунке 8. Рисунок 8 – Огива для интервального ряда
Объём выборки определяется по формуле (3): N=  4+4+4+4+4+4+3+3+3+4+3+3+3+4.= 50,Где: n- объем выборки ni- частота повторений . При заданных значениях группированного ряда получим: N=50,
Статистические характеристики определяются для группированного и интервального рядов отдельно!!
Относительная частота. Относительна частота определяется по формуле: W = ni/n = 4/50= 0,08, где n- объем выборки; ni – частота повторений. Для одного из значений группированного ряда получим: W = 0,08 , Значения относительных частот приведены в таблице 6. Таблица 6- Относительные частоты для группированного ряда
Среднее арифметическое Среднее арифметическое ряда определяется по формуле: X=  Для заданных исходных данных получим: X= 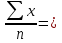 1/50*(1,26*4+3*4+8,6*4+10,2*4+24,2*4+40,9*4+42,1*3+44,9*3+55,3*3+56*4+66,7*3+92,6*3+93,6*3+100*4) =43,2448,Средневзвешенное Средневзвешенное значение статистического ряда определяется по формуле: X=  ,где Для заданных исходных данных получим: X=1,26*4+3*4+8,6*4+10,2*4+24,2*4+40,9*4+42,1*3+44,9*3+55,3*3+56*4+66,7*3+92,6*3+93,6*3+100*4/50=43,2448. Мода Мода – значение во множестве наблюдений, которое встречается наиболее часто. Мода для группированного ряда и для заданного ряда случайных величин имеет значение: M = 1,26; 3; 8,6; 10,2; 24,2; 40,9; 56; 100. Медиана Медианой называется – элемент выборки, которая делит пополам вариационный ряд на две части с одинаковым числом вариант в каждой. Медиана для группированного ряда имеет значение: Me =42,1+44,9/2 = 43,5. Дисперсия ряда Дисперсия – это среднее арифметическое значение квадратов отклонений отдельных вариант от их средней арифметической. Дисперсия может быть рассчитана по формуле: D = 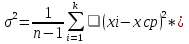 где – это значение корня квадратного из дисперсии.. Расчетные значения дисперсии для группированного ряда приведены в таблице 7 Таблица 7 – Расчет дисперсии ряда
D = 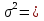 0,2*(31588,64+0+2692,56+0+20878,5+21613,83+12847,56+0+0+90369,73)= 0,02*179990,82 = 3599,81.Среднее квадратическое отклонение Среднее квадратическое отклонение – это значение корня квадратного из дисперсии. Среднее квадратическое отклонение рассчитывается по формуле: σ =  ,где D- дисперсия ряда, - среднее квадратическое отклонение. Для заданных исходных данных получим: σ =  = 59,99.Коэффициент вариации Коэффициент вариации определяется по формуле: δ =  где Xср- среднее значение. Для заданных исходных данных получим: δ = 59,99/50,63*100%= 118%. Характеристики описательной статистики Средствами программы Excel рассчитаны характеристики описательной статистики группированного ряда, числовые значения которых приведены на рисунке 5.
Рисунок 5 – Характеристики описательной статистики Вывод. Описательные статистики дают нам возможность оценить характер распределения данных в изучаемой выборке. На основании этой оценки мы можем принять решение о том, какие критерии надлежит использовать в дальнейшей работе – например, при сравнении выборок. Описательные статистики являются основой построения статистических графиков и диаграмм – например, диаграмм размаха, т.е. являются предварительным этапом в проведении визуального анализа данных. Таким образом, можно отнести их к категории разведочных методов анализа данных.
Относительная частота. Для одного из значений интервального ряда получим: W = 16/50 = 0,32 , Значения относительных частот приведены в таблице 6. Таблица 6- Относительные частоты для интервального ряда
Среднее арифметическое Для заданных исходных данных получим: X= 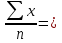(6,197+16,071+25,945+35,819+45,693+55,567+65,441+75,315+85,189+95,063)/10= 50,63 ,Средневзвешенное Средневзвешенное значение статистического ряда определяется по формуле: Для заданных исходных данных получим: X= (6,197*16)+(16,071*0)+(25,945*4)+(35,819*0)+(45,693*10)+(55,567*7)+(65,441*3)+(75,315*0)+(85,189*0)+(95,063*10)/50= 43,91 , Мода Мода – значение во множестве наблюдений, которое встречается наиболее часто. Мода для интервального ряда и для заданного ряда случайных величин имеет значение: M = 6,197. Медиана Медианой называется – элемент выборки, которая делит пополам вариационный ряд на две части с одинаковым числом вариант в каждой. Медиана для интервального ряда имеет значение: Me = ______ = ______. Дисперсия ряда Дисперсия – (определение). Дисперсия может быть рассчитана по формуле: D = 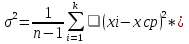Расчетные значения дисперсии для группированного ряда приведены в таблице 7 Таблица 7 – Расчет дисперсии ряда
D = (31558,66+0+2437,39+0+243,74+170,61+658,097+0+0+19742,91)*0,02= 1096,22. Среднее квадратическое отклонение Среднее квадратическое отклонение – является мерой случайных отклонений значений данных от среднего.. Среднее квадратическое отклонение рассчитывается по формуле: Для заданных исходных данных получим: σ =  = 33,109.Коэффициент вариации Коэффициент вариации определяется по формуле: Для заданных исходных данных получим: δ = 33,109/50,63*100%= 65,39%. Характеристики описательной статистики Средствами программы Excel рассчитаны характеристики описательной статистики заданного ряда, числовые значения которых приведены на рисунке 5.
Рисунок 5 – Характеристики описательной статистики Вывод. Описательные статистики дают нам возможность оценить характер распределения данных в изучаемой выборке. На основании этой оценки мы можем принять решение о том, какие критерии надлежит использовать в дальнейшей работе – например, при сравнении выборок. Описательные статистики являются основой построения статистических графиков и диаграмм – например, диаграмм размаха, т.е. являются предварительным этапом в проведении визуального анализа данных. Таким образом, можно отнести их к категории разведочных методов анализа данных. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||