Статистический анализ. стат анализ. 1 статистический анализ случайных величин статистический анализ одномерной последовательности случайных величин Цель работы
 Скачать 489.36 Kb. Скачать 489.36 Kb.
|
|
1 СТАТИСТИЧЕСКИЙ АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИН 1.1. Статистический анализ одномерной последовательности случайных величин Цель работы: приобрести компетенции статистического анализа одномерной последовательности случайных величин. Задание: Подготовить исходные данные. Построить вариационный, статистический, группированный ряды. Построить гистограмму, полигон, кумуляту, огиву. Определить относительные частоты последовательности. Определить: среднее арифметическое (по вариационному ряду), средневзвешенное (по группированному ряду), моду, медиану, дисперсию (по группированному ряду); среднее квадратическое отклонение , коэффициент вариации. Рассчитать в программе Excel характеристики описательной статистики для заданной последовательности случайных величин. Исходные данные В качестве исходных данных принята (назначить самостоятельно числовые характеристики из нефтегазовой сферы или в соответствии с вариантом задания, которые приведены в файле с заданиями) (табл. 1.1).
Таблица 1.1- Наименование случайной величины, е.и. Средствами программы Excel рассчитаны характеристики описательной статистики заданной последовательности значений случайной величины (в качестве исходных данных необходимо применять данные таблицы 1.1), числовые значения которых приведены на рисунке 1.1. Вариационный ряд Вариационный ряд – последовательность. , полученная в результате расположения в порядке не убывания исходной последовательности независимых одинаково распределённых случайных величин. Для заданной последовательности случайных величин вариационный ряд показан в таблице 1.2. Таблица 1.2- Вариационный ряд
Характеристики вариационного ряда: максимальное значение ряда Хmax = 26,9 ; минимальное значение ряда Xmin = 22,4 ; размах ряда определяется по формуле: R = Xmax – Xmin = 26,9-22,4 = 4.5. Характеристики статистических рядов Статистический ряд - это упорядоченное распределение единиц совокупности на группы по определённому варьирующему признаку. Статистические ряды могут быть: - группированными – например, группируются значения с одинаковыми величинами; - интервальными – группировка выполняется по количеству попаданий в интервал Группированный статистический ряд Группированным статистическим рядом называется последовательность пар. Группированный статистический ряд для заданных исходных данных приведен в табл. 1.3. Таблица 1.3 - Группированный статистический ряд
Графическое представление статистических характеристик группированного ряда Гистограмма для группированного ряда. Гистограмма - способ представления табличных данных в графическом виде Гистограмма по заданным значениям группированного ряда показана на рисунке 1.2. 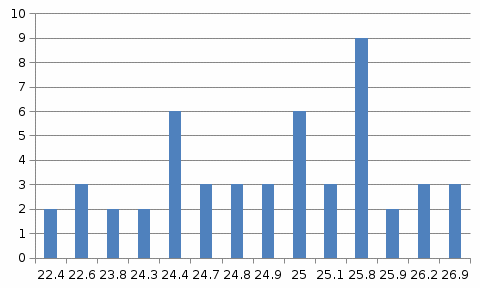 Рисунок 1.2 - Гистограмма для группированного ряда Полигон для группированного ряда Полигон – это ломаная, соединяющая точки. Полигон для группированного ряда показан на рисунке 1.3. 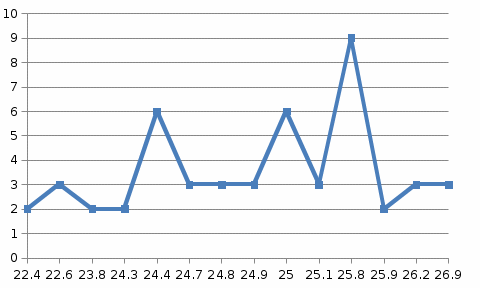 Рисунок 1.3 – Полигон для группированного ряда Кумулята для группированного ряда. Кумулята – графическое представление ряда статистических данных Кумулята для группированного показан на рисунке 1.4. Рисунок 1.4 – Кумулята для группированного ряда Огива для группированного ряда. Огива – графическое изображение ряда распределения по накопленным частотам (частостям), совпадет с кумулятой. Огива для группированного ряда показана на рисунке 1.5. 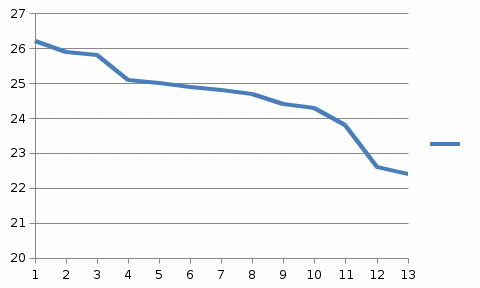 Рисунок 1.5 – Огива для группированного ряда Статистические характеристики группированного ряда Объем выборки группированного ряда. Объем выборки – это количество единиц попавших в выборочную совокупность. Объём выборки определяется по формуле: n = 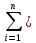 где: n – объем выборки; ni – частота повторений При заданных значениях ряда получим: n = 2+3+2+2+6+3+3+3+6+3+9+2+3=47 Относительная частота. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел Относительна частота определяется по формуле: W = 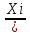 , ,Для первого значения ряда получим: W = 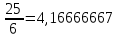 , ,Значения относительных частот приведены в таблице 1.4. Таблица 1.4- Относительные частоты для группированного ряда
Среднее арифметическое группированного ряда. Среднее арифметическое ряда- разновидность среднего значения Для заданных исходных данных получим: Xсв= 24,60769 Средневзвешенное группированного ряда. Средневзвешенное значение статистического ряда – математическое понятие, обобщающее среднее арифметическое. Средневзвешенное значение статистического ряда определяется по формуле: X= 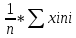 где ???? Для заданных исходных данных получим: X= 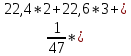 …) …)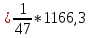 ≈ 24,81. ≈ 24,81.Мода группированного ряда Мода – числовое значение, частота повторений котрого наибольшая. Мода для группированного ряда и для заданного ряда случайных величин имеет значение: M = 25,8. Медиана группированного ряда. Медианой называется – элемент выборки, который делит вариационный ряд пополам, так, что эти части имеют одинаковое число элементов. Медиана соответствует варианту, стоящему в середине вариационного ряда. Медиана для группированного ряда рассчитывается по формуле: Me = 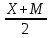 , ,При заданных значениях получим: Me = 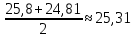 , ,Дисперсия группированного ряда. Дисперсия – мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Дисперсия может быть рассчитана по формуле: D =, где ?????. Данные для расчета дисперсии для других групп ряда приведены в таблице 1.5. Таблица 1.5 – Данные для расчета дисперсии ряда
Тогда дисперсия для группированного ряда определится так: D = ______________________________________________. Среднее квадратическое отклонение группированного ряда. Среднее квадратическое отклонение – (дать определение). Среднее квадратическое отклонение рассчитывается по формуле: σ = 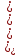 , ,где ????? Для заданных исходных данных получим: σ = ______ = _______. Коэффициент вариации группированного ряда Коэффициент вариации – (дать определение). Коэффициент вариации определяется по формуле: δ = 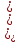 где ??????. Для заданных исходных данных получим: δ = ________= ______. Средствами программы Excel рассчитаны характеристики описательной статистики группированного ряда (в качестве исходных данных необходимо применять данные таблицы 1.3), числовые значения которых приведены на рисунке 1.6.  Рисунок 1.6 – Характеристики описательной статистики Вывод. (приводится сравнение расчетных значений, выполненных вручную и выполненной с помощью ПК) ________________________________________________________ Интервальный статистический ряд Интервальный ряд – (дать определение) . Для построения интервального ряда примем количество интервалов t = ______ Ширина интервалов определяется по формуле: rt =__________, где - ??????. При заданных исходных данных получим: rt = ___________. В таблице 1.6 показаны значения границ интервалов и средние значения величин кажого интервала . Таблица 1.6 – Значения границ интервалов
Интервальный ряд представлен в таблице 1.7. Таблица 1.7 - Интервальный ряд
Графическое представление статистических характеристик ряда Гистограмма интервального ряда. Гистограмма по средним значениям интервального ряда показана на рисунке 1.7. Полигон интервального ряда. Полигон для интервального ряда показан на рис. 1.8 Кумулята интервального ряда. Кумулята для интервального ряда показан на рисунке 1.9. Огива интервального ряда. Огива для интервального ряда показана на рисунке 1.10.  Рисунок 1.7 - Гистограмма для интервального ряда  Рисунок 1.8 – Полигон для интервального ряда  Рисунок 1.9 – Кумулята для группированного ряда  Рисунок 1.10 – Огива для интервального ряда Статистические характеристики интервального ряда. Объем выборки интервального ряда. При заданных значениях интервального ряда получим объём выборки: N= ___________________________.= _________, Относительная частота интервального ряда. Для первого значения интервального ряда получим: W = ___________________________.= _________, Значения относительных частот приведены в таблице 1.8. Таблица 1.8- Относительные частоты для группированного ряда
Среднее арифметическое интервального ряда. Для заданных исходных данных получим: Xср= __________________________ = ___________, Средневзвешенное интервального ряда. Для заданных исходных данных получим: Xсв = ______________________ = _____, Мода интервального ряда. Мода для интервального ряда и для заданного ряда случайных величин имеет значение: M = __________. Медиана интервального ряда. Медиана для интервального ряда имеет значение: Me = ______ = ______. Дисперсия интервального ряда. Расчетные значения дисперсии для группированного ряда приведены в таблице 1.9. Таблица 1.9 – Расчет дисперсии ряда
Тогда дисперсия для интервального ряда примет значение: D = ____________________________________. Среднее квадратическое отклонение интервального ряда Для заданных исходных данных получим: σ = ______ = _______. Коэффициент вариации интервального ряда Для заданных исходных данных получим: δ = ________= ______. Характеристики описательной статистики интервального ряда. Средствами программы Excel рассчитаны характеристики описательной статистики заданного ряда (для корректного расчета данных характеристик необходимо построить полный интервальный ряд для средних значений случайной величины в табл. 1.10). Таблица 1. 10- Полный интервальный ряд
Числовые значения, рассчитанные в программе Excel, приведены на рисунке 1.11.  Рисунок 1.11 – Характеристики описательной статистики Вывод. (аналогично разделу 3.1) ________________________________________________________ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
