Линейное программирование. 01. Линейное программирование. Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (озлп)

• Название: Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (озлп)
• Анкор: Линейное программирование
• Дата: 31.05.2022
• Размер: 111.9 Kb.
• Имя файла: 01. Линейное программирование.docx
• Тип: Задача; #560559

Линейное программирование

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Задачи

Общей (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида: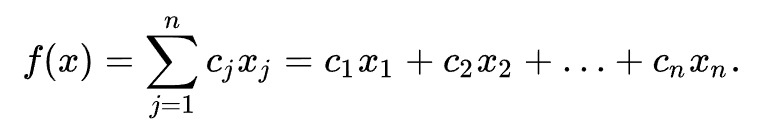



Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП)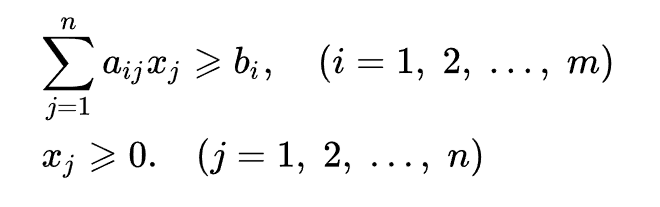



Задача линейного программирования будет иметь канонический вид, если в основной задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства: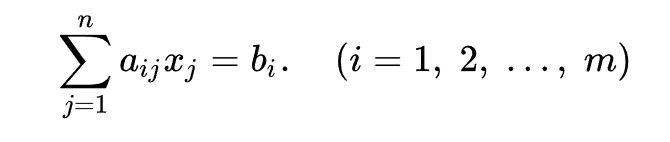



Основную задачу можно свести к канонической путём введения дополнительных переменных.

Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств.

Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты c с обратным знаком.

Несколько примеров задач, которые сводятся к задачам линейного программирования:

Задача оптимального раскроя материала. Фирма изготовляет изделие состоящее из р деталей. Причем в одно изделие эти детали входят в количествах k₁ ,..., k_r . С этой целью производится раскрой m партий материала. В i-ой партии имеется b_i единиц материала. Каждую единицу материала можно раскроить на детали n способами. При раскрое единицы i-ой партии j-м способом получается а_ijr деталей r-го вида. Требуется составить такой план раскроя материала, чтобы из них получить максимальное число изделий.

Транспортная задача. Имеется n поставщиков и m потребителей одного и того же продукта. Известны выпуск продукции у каждого поставщика и потребности в ней каждого потребителя, затраты на перевозки продукции от поставщика к потребителю. Требуется построить план транспортных перевозок с минимальными транспортными расходами с учетом предложения поставщиков и спроса потребителей.

Задача о назначениях на работу. Имеется n работ и n исполнителей. Стоимость выполнения работы i исполнителем jравна c_ij. Нужно распределить исполнителей на работы так, чтобы минимизировать затраты на оплату труда.

3адача о смесях (о рационе). Из m видов исходных материалов каждый из которых состоит из n компонент, составить смесь, в которой содержание компонент должно быть не меньше b₁ ,...,b_n. Известны цены единиц материалов с₁ ,...,с_m и удельный вес j-го компонента в единице i-го материала. Требуется составить смесь, в которой затраты будут минимальными.

Задача о рюкзаке. Имеется n предметов. Вес предмета i равен р_i , ценность – с_i (i=1,...,n). Требуется при заданной ценности груза выбрать совокупность предметов минимального веса.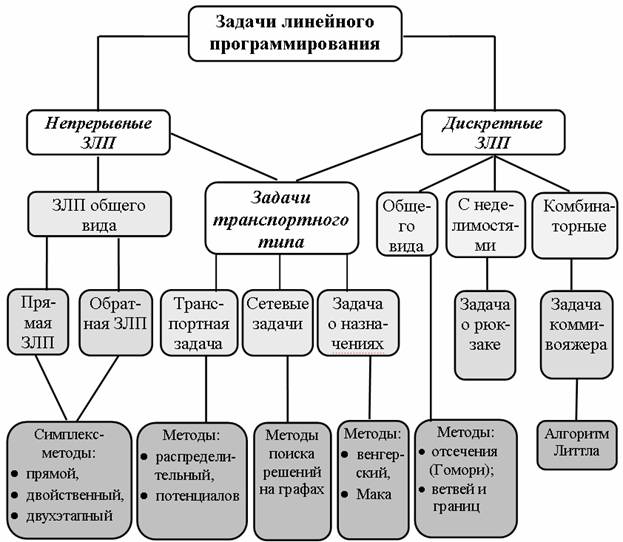