Надежность. надежность учебник. Задачи и исходные положения теории надежности 3 3 Причины и характер отказов объектов 8

• Название: Задачи и исходные положения теории надежности 3 3 Причины и характер отказов объектов 8
• Анкор: Надежность
• Дата: 27.03.2023
• Размер: 1.16 Mb.
• Имя файла: надежность учебник.doc
• Тип: Документы; #1018268
• страница: 6 из 17

1.8 Параллельное соединение элементов системы электроснабжения

Рисунок 1.6 –параллельное соединение элементов

Под группой параллельно включенных элементов будем понимать систему из n постоянно включенных в работу элементов (рис. 1.6), где m элементов обеспечивает нормальное функционирования группы, а n-m элементов являются постоянно включенном «горячим резервом».

Если параллельные по схеме элементы рассчитаны на неполную пропускную способность для покрытия нагрузки, то отказ любого элемента в каждой цепи вызывает одинаковые последствия в нарушении электроснабжения. Поэтому с точки зрения надежности эти элементы считаются соединенными последовательно.

Будем считать, что отказ еще одного элемента после отказа всех резервных приводит к отказу всей группы в целом. Таким образом, вероятность отказа группы определяется, как вероятность совпадения отказов (n-m+1) элементов в течении расчетного времени.

Если отказы одного элемента независимы от отказов других элементов, то, вероятность отказа системы равна:

(1.33)

При равнонадёжных элементах

(1.34)

При экспоненциальном законе распределения интенсивности отказов: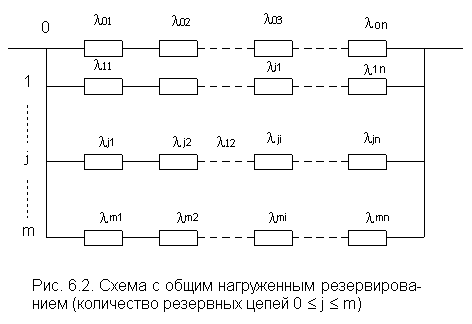

(1.35)



Рисунок 2.6 – Схема с общим нагруженным резервированием (количество резервных цепей 0 ≤ j ≤ m

На рис.1.7 изображена резервированная схема. Данная схема имеет основную (с индексом "0") электрическую цепь с "n" последовательно включенными элементами. Параллельно ей включено "m" резервных цепей, имеющих точно такие же параметры элементов, как и в основной цепи.

Вероятность безотказной работы системы с количеством цепей m + 1 равна

Р(t) = 1 - Q(t) = 1- [1- ]^m+1; (1.36)

В случае, когда λ_i = const, в каждой из цепей (поток отказов простейший) выражение , где

Тогда вместо выражения (1.36) можно записать:

(1.37)

где - вероятность безотказной работы основной цепи

Средняя наработка до отказа резервированной системы:

(1.38)

После некоторых преобразований получим

(1.39)

где i – номер параллельного элемента системы (параллельной цепи).

Интенсивность отказов системы определяется по выражению

(1.40)

Параллельное соединение работающих восстанавливаемых элементов



Рисунок 1.7 – Два параллельно соединенных элемента системы электроснабжения

Распишем состояние функционирование рассматриваемой системы с помощью функции вероятностью отказа и функции вероятности безотказной работы.



При пропускной способности S=(100%), первые три члена соответствуют рабочему состоянию системы и только последний член выражает одновременный отказ обоих элементов, то есть полный разрыв цепи.

Для двух параллельно соединенных элементов (рис. 2.7) с неизменным параметром потока отказа (при пропускной способности каждого из элементов S = 100%) вероятность безотказной работы равна:

Р(t) = ^(1.41)

При ω₁ = ω₂ = ω, Р(t) = 2

Вместо функций вероятности безотказной работы и функции вероятности отказа можно воспользоваться коэффициентами готовности и коэффициентами аварийности (простоя).

Тогда вероятность отказа рассматриваемой системы, можно найти по формуле:

(1.42)

Вероятность того, что система будет в рабочем состоянии

(1.43)

Для упрощения расчетов вероятности отказа и вероятности безотказной работы, можно воспользоваться аппроксимацией:

Есл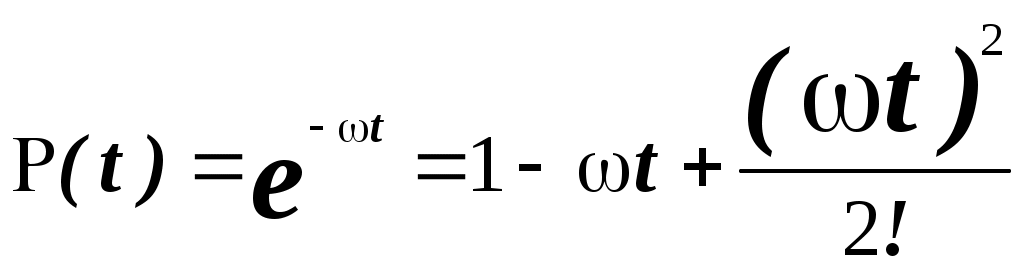и и ,

то можно принять:

и (1.44)

Если для последовательного соединения параметр потока отказов остается постоянным и равный сумме параметров потока отказов отдельных элементов, то для параллельного соединения, это уже не применимо.

Параметр потока отказа цепи из параллельного соединения элементов является временной функции работы, хотя среднее время между отказами (наработка на отказ) является величиной постоянной.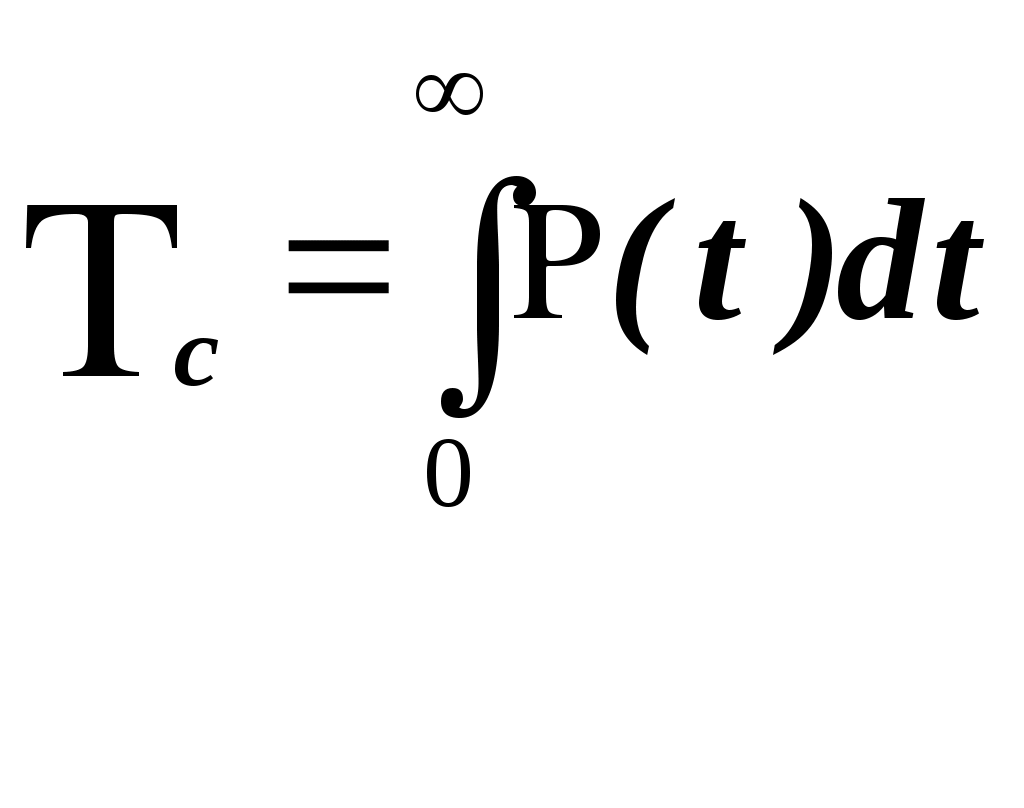



для двух элементов:

.

Если ω₁ =ω₂ = ω , то , для n элементов

Изложенное выше относится к нагруженному или постоянно включенному резерву, то есть для цепей, в которых резервные элементы несут постоянную нагрузку. Но возможно применение ненагруженного резерва, то есть такого резерва, когда резервные элементы подключаются автоматически при отказе рабочего элемента.



где: - вероятность того, что не произошло ни одного отказа;

- вероятность того, что произошел один отказ;

- вероятность того, что произошло два отказа;

Для многократной резервированной системы с невключенным резервом можно записать: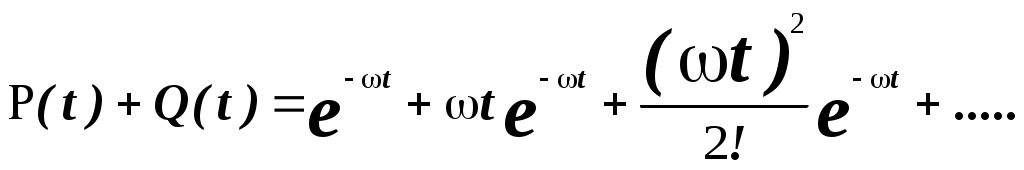



Если система состоит из одного работающего и второго такого же резервного элемента, то вероятность погашения обоих элементов будет равна:



Средняя наработка на отказ системы из двух элементов

(1.45)

Для случая, когда n -резервных линий резервируют одну линию или один элемент:

(1.46)