Метрология-учебник. Задачи интенсификации производства, стоящие перед промышленностью и наукой нашей страны, требуют создания новых и совершенствования имеющихся технологических процессов и материалов, строгого контроля качества продукции
 Скачать 1.92 Mb.
|
1.4. ПРИЧИНЫ В03НИКНОВЕНИЯ И СПОСОБЫ ИСКЛЮЧЕНИЯ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙПрирода и происхождение систематических погрешностей обычно обусловлены спецификой конкретного эксперимента. Поэтому обнаружение и исключение систематических погрешностей во многом зависит от мастерства экспериментатора, от того, насколько глубоко он изучил конкретные условия проведения измерений и особенности применяемых им средств и методов. Вместе с тем существуют некоторые общие причины возникновения систематических погрешностей, в соответствии с которыми их подразделяют на методические, инструментальные и субъективные. Методические погрешности происходят от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима исследуемого объекта (вследствие внесения термопары) . Инструментальные погрешности зависят от погрешностей применяемых средств измерения. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и т.д. являются причинами инструментальных погрешностей. Погрешности измерения возникают также из-за неправильной установки средства измерения, влияния на него магнитных или электрических полей, наличия дополнительных и динамических погрешностей. Дополнительные погрешности обусловлены отклонением условий, в которых работает прибор, от нормальных. Динамические погрешности возникают из-за инерционности применяемых технических средств при достаточно быстрых изменениях измеряемой величины. Все эти погрешности отличают от инструментальных (ГОСТ 8.009-84), поскольку они связаны не столько с самими средствами измерений, сколько с условиями, при которых они работают. Их устранение производится иными способами, нежели устранение инструментальных погрешностей. Субъективные погрешности вызываются неправильными отсчетами показаний прибора человеком (оператором), Это может случиться, например, из-за неправильного направления взгляда при наблюдении за показаниями стрелочного прибора (погрешность от параллакса). Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности. Систематические погрешности могут оставаться постоянными либо закономерно изменяться. В последнем случае их подразделяют на прогрессирующие (возрастающие или убывающие), периодические и изменяющиеся по сложному закону. Обнаружение причин и источников систематических погрешностей позволяет принять меры к их устранению или исключению посредством введения поправки . Поправкой называется значение величины, одноименной с измеряемой, которое нужно прибавить кполученному при измерении значению величины с целью исключения систематической погрешности. В некоторых случаях используют поправочный множитель—число, на которое умножают результат измерения для исключения систематической погрешности. Поправка или поправочный множитель определяется при помощи поверки технического средства, составления и использования соответствующих таблиц и графиков. Применяются также расчетные способы нахождения поправочных значений. Существуют специальные методы организации измерений, устраняющие систематические погрешности. К ним относятся, например, метод замещения и метод компенсации погрешности по знаку. Метод замещения заключается в том, что измеряемая величина замещается известной величиной, получаемой при помощи регулируемой меры. Если такое замещение производится без каких-либо других изменений в экспериментальной установке и после замещения установлены те же показания приборов, то измеряемая величина равняется известной величине, значение которой отсчитывается по указателю регулируемой меры. Этот прием позволяет исключить постоянные систематические погрешности. Погрешность измерения при использовании метода замещения определяется погрешностью меры и погрешностью, возникающей при отсчете значения величины, замещающей неизвестную. Метод компенсации погрешности по знаку применяется для исключения систематических погрешностей, которые в зависимости от условий измерения могут входить в результат измерения с тем или иным знаком (погрешность от термоЭДС, от влияния напряженности постоянного электрического или магнитного поля и др.). В этом случае можно провести измерения дважды так, чтобы погрешность входила в результаты измерений один раз с одним знаком, а другой раз—с обратным. Среднее значение из двух полученных результатов является окончательным результатом измерения, свободным от указанных выше систематических погрешностей. При проведении автоматических измерений широко используются схемные методы коррекции систематических погрешностей. Компенсационное включение преобразователей, различные цепи температурной и частотной коррекции являются примерами их реализации. Новые возможности появились в результате внедрения в измерительную технику средств, содержащих микропроцессорные системы. С помощью последних удается производить исключение или коррекцию многих видов систематических погрешностей. Особенно это относится к инструментальным погрешностям. Автоматическое введение поправок, связанных с неточностями градуировки, расчет и исключение дополнительных и динамических погрешностей, исключение погрешностей, обусловленных смещением нуля—эти и другие корректировки позволяют существенно повысить точность измерений. Следует, однако, заметить, что какая-то часть систематической погрешности, несмотря на все усилия, остается неисключенной. Эта часть входит в результат измерения и искажает его. Она может быть оценена исходя из сведений о метрологических характеристиках использованных технических средств. Если таких сведений недостаточно, то может быть полезным сравнение измеренных значений с аналогичными результатами, полученными в других лабораториях другими лицами. 1.5. ОЦЕНКА СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙАдекватным математическим аппаратом описания случайных погрешностей является теория вероятностей. Согласно последней случайная величина наиболее полно характеризуется своим законом распределения (или 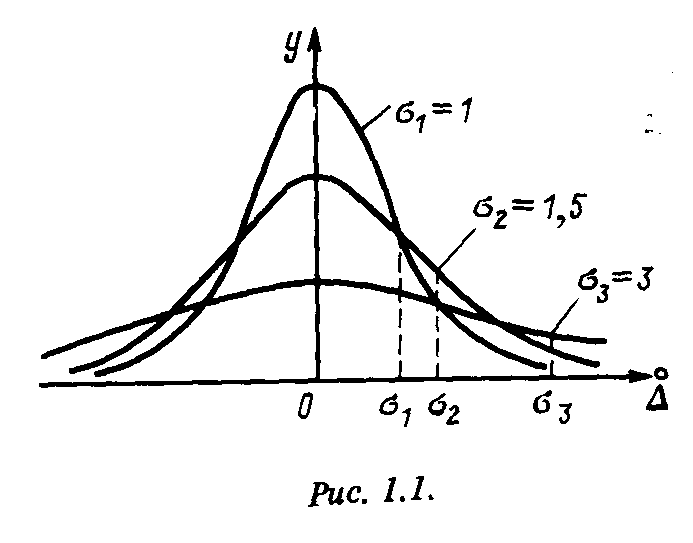 плотностью распределения) вероятностей. Измерителям чаще всего приходится принимать нормальную и равномерную плотность распределения. Возможны и другие законы распределения, которые обычно аппроксимируются стандартными функциями. Если выполняются предположения о том, что погрешности измерений могут принимать непрерывный ряд значений, при большом числе измерений частота появления погрешностей, равных по абсолютной величине, но различного знака, одинакова и малые погрешности встречаются чаще, чем большие, то тогда для описания случайных погрешностей следует применять нормальный закон распределения вероятностей, для которого (1.4) где — плотность вероятностей случайной погрешности ; — среднее квадратическое значение случайной погрешности. Кривые, соответствующие выражению (1.4) для разных значений , приведены на рис. 1.1. Видно, что при малых значениях о вероятней получить малую погрешность измерений, нежели при больших. Вероятность того, что погрешность результата измерения находится между заданными предельными значениями 1 , и 2 , вычисляется по формуле 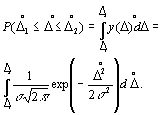 (1.5) Интеграл в формуле (1.5) можно вычислить, используя таблицы функции Лапласа , приводимые в книгах по теории вероятностей и статистической обработке экспериментальных результатов [2,28]. Нетрудно заметить, что (1.6) В табл. 1.1 приведены значения вероятностей для некоторых интервалов , заданных в единицах . Таблица 1.1
В первом столбце табл. 1.1 указываются интервалы, характеризуемые своими нижними и верхними границами и соответственно. Второй столбец дает вероятности P того, что случайная погрешность результата измерения не выходит за границы соответствующих интервалов. В третьем столбце показано, каковы вероятности выхода случайной погрешности за пределы интервалов. Согласно табл. 1.1 вероятности получения значения случайных погрешностей в интервале [-2/3,2/3] и за его пределами одинаковы, в то время как в среднем только 0,3% измерений имеют погрешности, абсолютное значение которых превышает 3 . Значение погрешности 2/3 называется вероятной погрешностью, а значение 3 часто считают практически наибольшей возможной погрешностью. Однако при большом числе измерений ( n>20 30) максимальная погрешность нередко может превышать 3 . Как уже указывалось, часто распределение погрешностей можно принять равномерным: 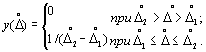 Такой закон распределения характерен, например, для погрешностей отсчета по шкале прибора, погрешностей дискретности в цифровых измерительных приборах, погрешностей квантования в аналого-цифровых преобразователях (АЦП). Рассмотрим далее оценки параметров распределения случайных погрешностей прямых измерений. Напомним, что случайная абсолютная погрешность определяется формулой , где x— результат измерения; x и — истинное значение измеряемой величины. Если было проведено n прямых измерений одной и той же величины, то в общем случае в каждом из актов измерений погрешность будет разной : , где — погрешность i -го измерения; xi— результат i- го измерения. Поскольку истинное значение измеряемой величины x и неизвестно, непосредственно случайную абсолютную погрешность вычислить нельзя. При практических расчетах приходится вместо x и использовать его оценку. Обычно принимают, что истинное значение равно среднему арифметическому значению ряда измерений: (1.7) где xi— результаты отдельных измерений; n— число измерений. Теперь аналогично можно определить отклонение результата каждого измерения от среднего значения как (1.8) а затем по формуле (1.9) вычислить оценку значения среднеквадратической погрешности данного ряда измерений. Согласно теории вероятностей при достаточно большом числе измерений, имеющих независимые случайные погрешности, оценка сходится по вероятности к . Таким образом, (1.10) Ввиду того что среднее арифметическое значение также является случайной величиной, имеет смысл понятие среднеквадратического отклонения среднего арифметического значения . Эту величину обозначим символом . Можно показать, что для независимых погрешностей (1.11) Значение ср характеризует степень разброса . Как указывалось выше, выступает оценкой истинного значения измеряемой величины, т.е. является конечным результатом выполняемых измерений. Поэтому ср называют также средней квадратической погрешностью результата измерений. На практике значением , вычисляемым по (1.10), пользуются в том случае, если необходимо дать характеристику точности применяемого метода измерения: если метод точен, то разброс результатов отдельных измерений мал, т.е. мало значение Значение же ср вычисляемое по (1.11), используется для характеристики точности результата измерений некоторой величины, т.е. результата, полученного посредством математической обработки итогов целого ряда отдельных прямых измерений. Введем важные понятия доверительной вероятности и доверительного интервала. Как указывалось выше, среднее арифметическое значение , полученное в результате некоторого ряда измерений, является оценкой истинного значения x и и, конечно, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть P Д есть вероятность того, что отличается от x и не более чем на , т.е. или Вероятность P Д называется доверительной вероятностью, а интервал значений измеряемой величины от до — доверительным интервалом. Приведенные выше неравенства означают, что с вероятностью P Д доверительный интервал от до заключает в себе истинное значение x и Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами — доверительной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал. В частности, при достаточно большом числе измерений часто бывает оправданным использование нормального закона, в то время как при небольшом числе измерений ( n<20) , результаты которых принадлежат нормальному распределению, следует пользоваться распределением Стьюдента. Это распределение имеет плотность вероятностей, практически совпадающую с нормальной при больших n, но значительно отличающуюся от нормальной при малых n. В табл. 1.2 приведены так называемые квантили распределения Стьюдента для числа измерений n=230 и доверительных вероятностей P Д =0,8 0,99 . Более полную таблицу можно найти, например, в [2]. Укажем, однако, что обычно таблицы распределения Стьюдента приводятся не для значений n и , а для значений m=n-1 и =1-P Д , что следует учитывать при пользовании ими. Чтобы определить доверительный интервал, надо для данных n и P Д найти квантиль и вычислить величины и Ттаблица 1.2. Квантили распределения Стьюдента
которые будут являться верхней и нижней границами доверительного интервала. Примеры нахождения доверительных интервалов для заданной доверительной вероятности приведены ниже. Там же показана одна из наиболее употребительных форм записи результата измерения в виде где — результат измерения в единицах измеряемой величины; — погрешность измерения; В и Н — верхняя и нижняя границы погрешности измерения; P Д — доверительная вероятность. Пример 1. Произведено 17 отсчетов значений измеряемой величины — напряжения (см. ниже). Требуется произвести обработку результатов измерений (предполагая их нормальное распределение). Для этого выбрать доверительную вероятность P Д =0.95 . Систематической погрешностью пренебречь.
— номер измерения, xi— результат измерения. Обработку результатов измерений будем вести в следующей последовательности. 1. Определим среднее арифметическое значение результатов отдельных измерений по формуле (1.7): = (1681 + 1701 + 1693 + 1678 + 1686 + 1674 + 1705 + 1685 + 1697 + + 1690 + 1690 + 1685 + 1682 + 1690 + 1687 + 1680 + 1692) /17 = = 1688,0 мВ. Значение будем считать оценкой истинного значения измеряемого напряжения U, т.е. U= 1688,0 мВ. 2. Вычислим отклонения результатов отдельных измерений от среднего значения по формуле (1.8):
3. Вычислим оценку значения средней квадратической погрешности ряда измерений по формуле (1.9): 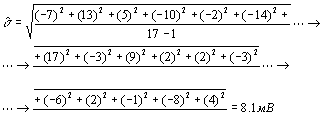 Согласно (1.10) =8,1 мВ. Далее по (1.11) определим ср =8,1/ 17 2,0 мВ. Для вычисления доверительного интервала, соответствующего доверительной вероятности P Д = 0,95 и числу измерений n= 17, следует воспользоваться табл. 1.2. Находим значение квантиля: Поскольку ср = 2мВ , то нижняя граница доверительного интервала  а верхняя граница  Нижняя и верхняя границы погрешности измерения и соответственно. Результат измерения может быть записан в виде U= 1688мВ; =+4мВ; РД =0,95. Пример 2. Произведено 10 отсчетов значений измеряемой величины—напряжения (см. ниже). Задание то же, что и в примере 1.
Следуя той же последовательности действий что и в примере 1, получим = 1689,0мВ, т.е. U = 1689,0мВ; 10мВ, т.е. = 10мВ; ср=3,2мВ. Находим из табл. 1.2 значение . Следовательно, границы доверительного интервала x н =1689,0-2,26 3,2=1681,8=1682мВ ; x в = 1689,0+2,26 3,2=1696,2=1696мВ. Результат измерения записывается в виде U= 1689мВ ; = 7 мВ ; P Д =0,95. Сравнение результатов измерения в примерах 1 и 2 показывает, что при уменьшении числа измерений с 17 до 10 происходит увеличение доверительного интервала, соответствующего одной и той же доверительной вероятности P Д =0,95. Случайные погрешности косвенных измерений. Если величина А является функцией величин Х, У,..., Z [А= f (Х, У,..., Z]и определяется на основании прямых измерений этих величин, то средняя квадратическая погрешность измерения величины А может быть вычислена по формуле  (1.12) где X, Y ,…, Z— средние квадратические погрешности измерения величин Х, У,... , Z соответственно. Производные вычисляются в точке (Х, У,..., Z) . Формула (1.12) справедлива в том случае, если величины Х, У,..., Z независимы (или некоррелированы). Суммирование погрешностей. При измерениях может быть несколько источников как систематических, так и случайных погрешностей. Поэтому практически важным является вопрос о правилах нахождения суммарной погрешности измерения по известным значениям погрешностей составляющих ее частей. При суммировании составляющих неисключенной систематической погрешности их конкретные реализации можно рассматривать как реализации случайной величины. Если известны границы i составляющих неисключенной систематической погрешности, а распределение этих составляющих в пределах границ равномерно, то граница неисключенной систематической погрешности результата измерения вычисляется по формуле где k —коэффициент, определяемый принятой доверительной вероятностью. При доверительной вероятности 0,95 он принимается равным 1,1 (ГОСТ 8.207-76) . При суммировании случайных погрешностей необходимо учитывать их корреляционные связи. Суммарная средняя квадратическая погрешность при двух составляющих может быть вычислена по формуле (1.13) где 1 , и 2 —средние квадратические погрешности отдельных составляющих; — коэффициент корреляции. Поскольку на практике трудно получить удовлетворительную оценку коэффициента , приходится ограничиваться крайними случаями, т.е. считать, что либо , либо 1. Тогда приведенная выше формула примет вид если =0 или если 1. Таким образом, при отсутствии корреляционной связи средние квадратические погрешности складываются геометрически, а в случае жесткой корреляционной зависимости—алгебраически. Этот вывод справедлив и для случая нескольких источников погрешностей. Правила нахождения границы погрешности результата измерения при одновременном наличии как неисключенных систематических, так и случайных погрешностей также регламентируются ГОСТ 8.207-76 и заключаются в следующем. Если < 0,8, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата где —коэффициент Стьюдента, определяемый по табл. 1.2. Если > 8, то, наоборот, пренебрегают случайной погрешностью по сравнению с систематической и считают, что граница погрешности результата . В случае, если эти неравенства не выполняются, следует найти композицию распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины, вычислить значение среднего квадратического отклонения и затем границы суммарной погрешности результата измерения. Допускается также определение границы погрешности результата измерения при помощи приведенных в ГОСТ 8.207-76 эмпирических формул. Исключение грубых погрешностей. Выделение грубых погрешностей (промахов) не простая задача, она требует достаточно глубокого понимания особенностей поведения измеряемой величины. Наиболее часто для обнаружения промаха используют так называемый критерий Райта. Согласно этому критерию, если случайное отклонение какого-либо измерения от среднего арифметического значения превышает З , то есть основание считать, что данное измерение содержит промах. Критерий Райта в таком виде целесообразно применять при не очень большом числе измерений n 20). Если же число измерений 20 <n100, то рекомендуется вместо значения З использовать значение 4 . Более обоснованная, хотя и более громоздкая процедура исключения грубых погрешностей базируется на одном из разделов математической статистики—статистической проверке гипотез. В связи с тем что не предполагается знания читателем соответствующего материала, авторы вынуждены отослать интересующихся к одному из курсов, посвященных специально вопросу обработки экспериментальных результатов [28 ]. Необходимое число измерений. Вопрос о том, сколько измерений требуется произвести для того, чтобы погрешность не превышала допустимое значение, весьма важен, так как от его решения зависит весь последующий ход эксперимента. Надо четко понимать, что увеличением числа измерений можно уменьшить только случайную составляющую погрешности (уменьшить средние квадратические погрешности и ср, которые согласно формулам (1.10) и (1.11) зависят от числа измерений n ) . В то же время систематическая погрешность не уменьшается при увеличении n. Поэтому если остаточная систематическая погрешность является преобладающей, то увеличение числа измерений мало что дает. Чаще всего в этом случае ограничиваются одним измерением. Так, например, при измерении напряжения сети неточным переносным стрелочным прибором нет никакого смысла прибегать к многократным измерениям и статистической обработке результатов измерения. Поскольку систематические погрешности заведомо превышают случайные, то достаточно провести всего одно измерение. При более точных измерениях на первый план могут выступить случайные погрешности. Тогда проведение многократных измерений является оправданным. Число измерений нужно выбрать таким, чтобы средняя квадратическая случайная погрешность ср не превышала максимального допускаемого значения ср , доп. Ясно, однако, что уменьшение ср за счет многократных измерений следует добиваться только до тех пор, пока вклад случайных погрешностей в общую погрешность измерения не будет сравним со вкладом остаточных систематических погрешностей. 1.6. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ И ПРЕОБРАЗОВАТЕЛЕЙВходной величиной измерительного прибора является его измеряемая величина. Наибольшее и наименьшее значения измеряемой величины, для которых нормированы погрешности, называются пределами измерения. Область значений, заключенная между верхним и нижним пределами измерения, называется диапазоном измерений. От диапазона измерений следует отличать диапазон показаний, который охватывает область значений шкалы, ограниченную конечным и начальным значениями шкалы. Таким образом, диапазон измерений, охватывающий часть шкалы, в пределах которой измерения могут быть проведены с нормируемой погрешностью, более узок, чем диапазон показаний, охватывающий всю шкалу. Выходной величиной измерительного прибора является изменение состояния отсчетного устройства, например положения стрелки стрелочного прибора. Функция (уравнение) преобразования—функциональная зависимость между выходной величиной у и входной величиной х. Как и любая функция, функция преобразования может задаваться аналитически (уравнением), таблично или графически. В аналитическую функцию преобразования обычно входят конструктивные параметры прибора или преобразователя и поэтому она используется при расчете и проектировании. Функция преобразования реального преобразователя определяется экспериментально. В ходе опыта определяется зависимость выходной величины от входной. Для упрощения анализа полученной функции по табличным данным строится график. Обычно желательно, чтобы функция преобразования была линейной. Чувствительность—это отношение изменения выходной величины измерительного прибора или измерительного преобразователя к вызвавшему ее изменению входной величины. Чувствительность определяется выражением (1.14) и может быть определена при любом способе задания функции преобразования. В важном частном случае, когда выходная величина изменяется пропорционально входной, S =у/х, где у—значение выходной величины, соответствующее входной величине х. При нелинейной функции преобразования чувствительность зависит от значения входной величины. Для прибора или преобразователя может определяться абсолютная, относительная и приведенная погрешности. Абсолютная погрешность прибора в данной точке диапазона измерения равна (1.15) где хП—показание прибора; х—истинное значение измеряемой величины. Однако в связи с тем, что истинное значение неизвестно, на практике вместо него используется действительное значение хД . В качестве хДпринимают показания более точного, образцового прибора. Абсолютная погрешность прибора выражается в тех же единицах, что и измеряемая величина. Относительная погрешность прибора равна отношению абсолютной погрешности к истинному значению измеряемой величины и обычно выражается в процентах: (1.16) Приведенная погрешность прибора также выражается в процентах и равна отношению абсолютной погрешности к нормирующему значению х N , которое принимается равным верхнему пределу измерений (если нулевая отметка находится на краю или вне шкалы) или диапазону измерения (если нулевая отметка находится внутри диапазона измерений), % : (1.17) Значения абсолютной, относительной и приведенной погрешностей используются для нормирования погрешности приборов. Абсолютную погрешность измерительного преобразователя невозможно определить по выражению (1.15), поскольку входная и выходная величины могут иметь различную физическую природу, а также вследствие того что часто отсутствует образцовый измерительный преобразователь, по которому можно было бы проверить рабочий преобразователь. Различают номинальную функцию преобразования измерительного преобразователя уном =f ном(х) которую он должен иметь согласно государственным стандартам, техническим условиям или другим нормативным документам, и реальную у= f (х), которую он имеет в действительности. Разность значений действительной и номинальной функций преобразования при одном и том же значении входной величины определяет абсолютную погрешность преобразователя по выходу: (1.18) Погрешность создается преобразователем. Однако часто бывает полезно знать значение входного сигнала, соответствующего погрешности преобразователя. Абсолютным значением погрешности преобразователя по входу называется разность (1.19) где х—истинное значение входной величины; x ном—значение входной величины, определяемое по номинальной функции преобразования уном =f ном(х), при значении выходной величины уном , соответствующей истинному значению х. Относительные погрешности по выходу и входу определяются соответственно равенствами (1.20) и (1.21) Приведенные погрешности по выходу и входу (1.22) и (1.23) где х maxи у max— максимальные значения входной и выходной величин, а xmin и у min— их минимальные значения. Очевидно, при пропорциональной функции преобразования у= S(x) значения относительных погрешностей так же как и приведенных погрешностей по входу и выходу совпадают. В технике часто используются преобразователи с линейной функцией преобразования (1.24) где S —чувствительность преобразователя; y0— значение выходной величины при нулевом значении входной. Отклонение такой функции преобразования от номинальной может быть вызвано отклонением y0 и отклонением чувствительности S . Погрешность, обусловленная неноминальным значением выходной величины при нулевом значени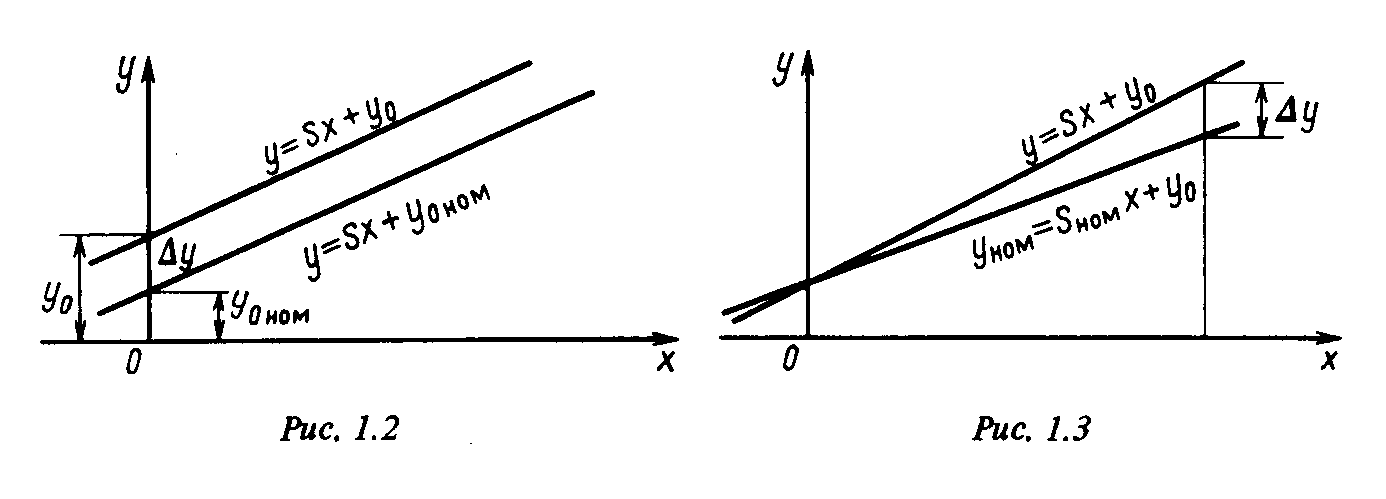и  входной y0, называется аддитивной . Погрешность, обусловленная неноминальным значением чувствительности S , называется мультипликативной. Аддитивная погрешность не зависит от входной величины. При изменении y0вследствие каких-либо причин график функции преобразования перемещается параллельно самому себе (рис. 1.2) . Значение этой погрешности (1.25) где у 0 ном — номинальное значение у 0. При мультипликативной погрешности наклон прямой, графически отображающий функцию преобразования, отличается от наклона при номинальной функции преобразования (рис. 1.3) . При этом абсолютная погрешность у=у—у 0зависит от входной величины х . Действительно, пусть чувствительность изменилась на S и стала равной S=S ном + S , где S ном—номинальное ее значение. В этом случае абсолютная погрешность преобразователя (1.26) т.е. абсолютная мультипликативная погрешность пропорциональна входной величине х . Рассмотрим относительную мультипликативную Погрешность при пропорциональной функции преобразования у= S ном (x): (1.27) Относительная мультипликативная погрешность равна относительному изменению чувствительности. Погрешность измерительных средств зависит от условий проведения измерений. При этом различают основную и дополнительные погрешности. Основной погрешностью называется погрешность, существующая при так называемых нормальных условиях, которые указаны в нормативных документах, регламентирующих правила испытания и эксплуатации данного средства измерения. Например, под нормальными условиями могут пониматься: температура окружающей среды (+ С; положение прибора горизонтальное с отклонением от горизонтального, не превышающем С; относительная влажность (65 15)% , практическое отсутствие магнитных и электрических полей; частота питающей сети (50 1) Гц и т.д. Дополнительная погрешность возникает при отклонении условий испытания и эксплуатации средства измерения от нормальных. Она нормируется значением погрешности, вызванной отклонением одной из влияющих величин от ее нормального значения или выходом ее за пределы нормальной области значений. Например, приведенная погрешность прибора при нормальных условиях, т.е. в диапазоне температур (+20 С , не превышает 1 % . Если температура лежит вне указанного диапазона, то погрешность может быть больше указанной. Например, приведенная дополнительная погрешность при изменении температуры на 10 С не должна превышать 1%. Нормирование погрешности средств измерения производится по максимально допускаемым значениям основной и дополнительной погрешностей (ГОСТ8.401-80). Погрешность средств измерения не должна превышать одного из перечисленных ниже пределов. а) Если погрешность имеет аддитивный характер, то предел допускаемой абсолютной погрешности не должен превышать (1.28) б) Если погрешность имеет как аддитивную, так и мультипликативную составляющую, то предел допускаемой абсолютной погрешности не должен превышать (1.29) в) Если погрешность имеет мультипликативный характер, то предел допускаемой относительной погрешности не должен превышать (1.30) г) Если погрешность имеет как аддитивную, так и мультипликативную составляющие, то предел допускаемой относительной погрешности (в процентах) не должен превышать (1.31) где a, b,c и d— постоянные; x к—конечное значение диапазона измерения. Из (1.31) следует, что при х=0 предел абсолютной погрешности (1.32) а при x=x к (1.33) д) Приведенная погрешность не должна превышать значения (1.34) При нормировании погрешности средства измерения постоянные а, b , с, d выбираются из следующего ряда чисел: 1 10n;1,5 10n;2 10n; 2,5 10n; 4 10n; 5 10n; 6 10n, где n=1; 0; -1; - 2 и т.д. Средствам измерения присваивается класс точности. Это обобщенная метрологическая характеристика, определяемая пределами допускаемых основной и дополнительных погрешностей, значения которых устанавливаются в стандартах на отдельные виды средств измерения. Класс точности обозначается числом, соответствующим нормированной основной погрешности средства измерения. Для случая ( r ) класс точности обозначается в виде дроби с/ d например: 0,1 /0,05. Класс точности стрелочных и самопишущих приборов, как правило, обозначается одним числом, равным максимально допускаемому значению основной приведенной погрешности с, тогда как класс точности цифровых приборов, мостов и компенсаторов указывается в виде дроби с/ d. Конкретные ряды классов точности устанавливаются в стандартах на отдельные виды средств измерения. Отдельными характеристиками погрешности являются вариации показаний прибора и порог чувствительности. Вариация показаний прибора—это наибольшая разность его показаний при одном и том же значении измеряемой величины. Основной ее причиной является трение в опорах подвижной части прибора. Вариацию определяют, сравнивая показания прибора, считанные один раз после установки требуемого значения измеряемой величины подходом снизу (со стороны меньших значений), а другой раз—подходом сверху (со стороны больших значений). Порог чувствительности—это изменение измеряемой величины, вызывающее наименьшее изменение показаний, различимое при нормальном для данного прибора способе отсчета. Собственное потребление мощности прибором из цепи, в которой производится измерение, является важной характеристикой прибора. Оно приводит к изменению электрических параметров этой цепи и отрицательно влияет на точность измерения. Особенно сильно это проявляется при измерениях в маломощных цепях. В зависимости от устройства, конструкции и назначения прибора потребляемая им мощность может колебаться от 1 0-12 Вт до нескольких ватт. Динамические характеристики. Описанные выше характеристики являются статическими, т.е. не зависящими от времени. Они, строго говоря, имеют смысл только в том случае, если параметры измерительного прибора (или другого средства измерения) и значение измеряемой величины остаются постоянными, а время измерения не ограничено. На практике, однако, эти условия часто не соблюдаются: измеряемая величина меняется по времени, измерение обычно нужно проводить за возможно более короткое время, параметры измерительного прибора только приближенно можно считать неизменными. Одновременный учет всех этих особенностей процесса измерения затруднителен. Имеется, однако, много случаев, когда о законе изменения входной величины за время измерения могут быть высказаны достаточно обоснованные предположения и когда средство измерения является линейной системой, т.е. может быть характеризовано линейным дифференциальным уравнением с постоянными коэффициентами: (1.35) где а 0 , а 1,...,an— постоянные коэффициенты . Нередко можно считать, что до момента времени t =0 входная величина была постоянной и начала изменяться лишь при t =0. Если при этом отсчитывать значения входной величины от значения, которое она имела до t =0, то получим нулевые начальные условия. Такое рассмотрение упрощает определение реакции звена у( t) на изменение входной величины. При нулевых начальных условиях уравнение (1.35) в операторной форме имеет вид (1.36) где р = p/dt— оператор. Передаточной функцией преобразователя называется отношение изображений по Лапласу выходной величины к входной: (1.37) Зная передаточную функцию преобразователя, можно определить его реакцию у( t) на заданное изменение измеряемой величины х( t) и определить динамическую погрешность (1.38) где у( t)— значение выходной величины измерительного средства в момент времени t; уст — значение выходной величины, заданное его статической функцией преобразования. При анализе динамических характеристик используются следующие типовые входные воздействия.
(1.39) где L-1 —символ обратного преобразования Лапласа. 2. Гармоническая функция. При гармоническом изменении входной величины , где Х m— амплитуда ее изменения; —ее круговая частота, выходная величина изменяется также гармонически: где У m —амплитуда выходной величины. Отношение реакции преобразователя ко входному воздействию определяет частотную передаточную функцию (комплексную чувствительность (1.40) где А( ) —модуль частотной передаточной функции; —сдвиг фаз между входной и выходной величинами. Связь между частотной передаточной функцией и передаточной функцией выражается соотношением при p = j . (1.41) Зависимость модуля частотной передаточной функции от частоты А( ) определяет амплитудно-частотную характеристику преобразователя; зависимость ее аргумента от частоты ) определяет фазочастотную характеристику. К важным динамическим характеристикам приборов относится время установления показаний—промежуток времени, прошедший с момента подключения или изменения измеряемой величины до момента, когда отклонение указателя от установившегося значения не превышает 1,5% длинны шкалы. Для многих приборов это время не превышает 4с. Временем установления показаний характеризуются показывающие приборы, имеющие указатель и шкалу. Для цифровых приборов указывается время измерения, отсчитываемое от начала измерения или изменения измеряемой величины, до получения результата на отсчетном устройстве с нормированной погрешностью. Обычно стремятся иметь приборы, обеспечивающие малые времена установления показаний (в случае цифровых приборов—малые времена измерения). Надежность прибора—способность сохранять заданные характеристики при определенных условиях в течение заданного времени. Выход значения параметров и характеристик прибора за пределы нормы считается отказом. Отказ измерительного прибора может наступить, если его действительная погрешность станет больше ее нормирующего значения, определяемого классом точности. Количественным показателем надежности является наработка на отказ—среднее время безотказной работы прибора. Наработка на отказ является статистической величиной. Она устанавливается для данной серии приборов на основании выборочных испытаний небольшой их партии, входящих в эту серию. Согласно ГОСТ 22261—82 приборы характеризуются также их механической и электрической прочностью, сопротивлением изоляции и некоторыми другими параметрами. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||