момент. Осциллятор и Момент Импульса. Vi. Квантовая теория гармонических колебаний и волн

• Название: Vi. Квантовая теория гармонических колебаний и волн
• Анкор: момент
• Дата: 15.12.2021
• Размер: 1.55 Mb.
• Имя файла: Осциллятор и Момент Импульса.doc
• Тип: Закон; #304460
• страница: 1 из 7

Глава VI. Квантовая теория гармонических колебаний и волн

Квантовая теория гармонических колебаний чрезвычайно важна в силу фундаментальности своих приложений. В классической физике все виды колебаний имеют общие закономерности. Наиболее простыми и фундаментальными являются гармонические колебания, которые могут иметь различную природу. Ещё более универсален характер гармонических колебаний в квантовой теории. Рассмотрим несколько примеров.

Пример 1: Квантовая электродинамика.

Согласно корпускулярно-волновому дуализму монохроматической волне, задаваемой и волновым вектором , можно поставить в соответствие квант поля, энергия которого , а импульс . Таким образом, энергия монохроматической волны пробегает дискретный ряд значений

С динамической точки зрения, свободное электромагнитное поле, находящееся в некотором объёме, эквивалентно системе независимых гармонических колебаний – гармонических осцилляторов (мод поля).

Таким образом, если мы построим квантовую теорию гармонических осцилляторов, то мы построим и квантовую теорию поля.

Пример 2: Квантовая теория колебаний кристаллической решётки.

Введём понятие идеальной кристаллической решётки. Если a – период решётки, то есть наиболее вероятные положения ядер.

Пусть u – смещение ядра относительно положения равновесия. Если , то колебания решётки с большой степенью точности можно считать гармоническими. Следовательно, колебания решётки в кристалле можно представить в виде совокупности независимых гармонических осцилляторов, задаваемых законом дисперсии .

Упругой волне в кристалле частоты ставятся в соответствие кванты-фононы с энергией и импульсом .

Пример 3: Квантовая теория колебаний атомов в молекуле.

С достаточной степенью точности можно рассматривать колебания атомов в молекуле как гармонические. Следовательно, колебания атомов в молекуле есть совокупность независимых гармонических осцилляторов.

Пример 4: Частица в потенциальной яме.

Одномерное движение квантовой частицы в параболической потенциальной яме есть гармонический осциллятор.

Гармонические колебания определяются частотой , и все особенности колебаний в квантовой теории определяются частотой и зависят от неё. Следовательно, основные выводы квантовой теории гармонических колебаний и волн не зависят от физической природы гармонического осциллятора.

Перейдём теперь к изложению последовательной квантовой теории гармонических колебаний отдельного осциллятора. Для определённости будем рассматривать одномерное движение нерелятивистской частицы в параболическом потенциале.

§ 17. Спектр значений энергии гармонического осциллятора

Основная задача заключается в определении спектра значений энергии гармонического осциллятора. Исходным является уравнение

(17.1)

Потенциальная энергия гармонического осциллятора равна 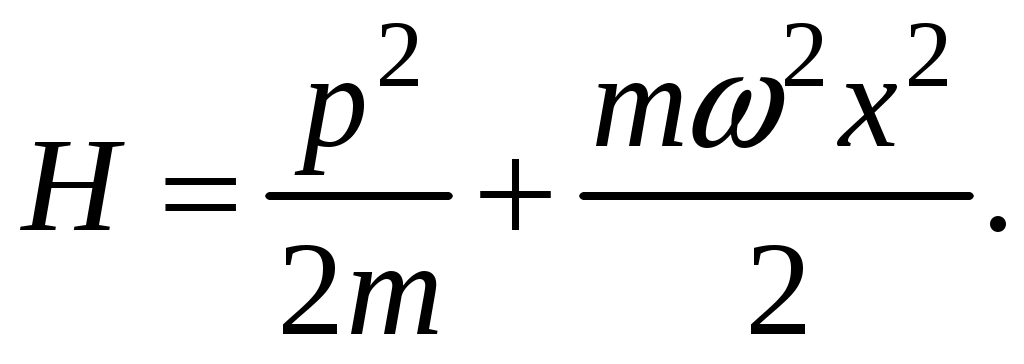, где – собственная частота колебаний, а кинетическая энергия есть . Следовательно, гамильтониан осциллятора запишется в виде

(17.2)

Поскольку потенциальная энергия обращается в бесконечность при , гармонический осциллятор может совершать лишь финитное движение (в ограниченной области пространства). Благодаря этому, энергетический спектр осциллятора дискретен. Из вида операторов , и следует, что .

Существует несколько способов решения задачи об определении спектра энергии:

1. 
   координатное представление;
   
2. 
   импульсное представление;
   
3. 
   матричный метод;
   
4. 
   операторный метод.
   

Из перечисленных подходов к решению задач операторный метод является наиболее общим, позволяющим перейти к описанию квантованных полей. В операторном методе для определения спектра значений энергии гармонического осциллятора используются лишь перестановочные соотношения для канонически сопряжённых переменных и :



Универсальность теории гармонического осциллятора и её независимость от физической природы станет очевидной после перехода к безразмерным переменным и :



Заметим, что для гармонического осциллятора частоты имеется единственная величина, имеющая размерность энергии , а так как имеет размерность энергии, то .

Найдём вид оператора . Поскольку выражение имеет размерность энергии, т.е. , можно записать, что или

(17.3)

Аналогично 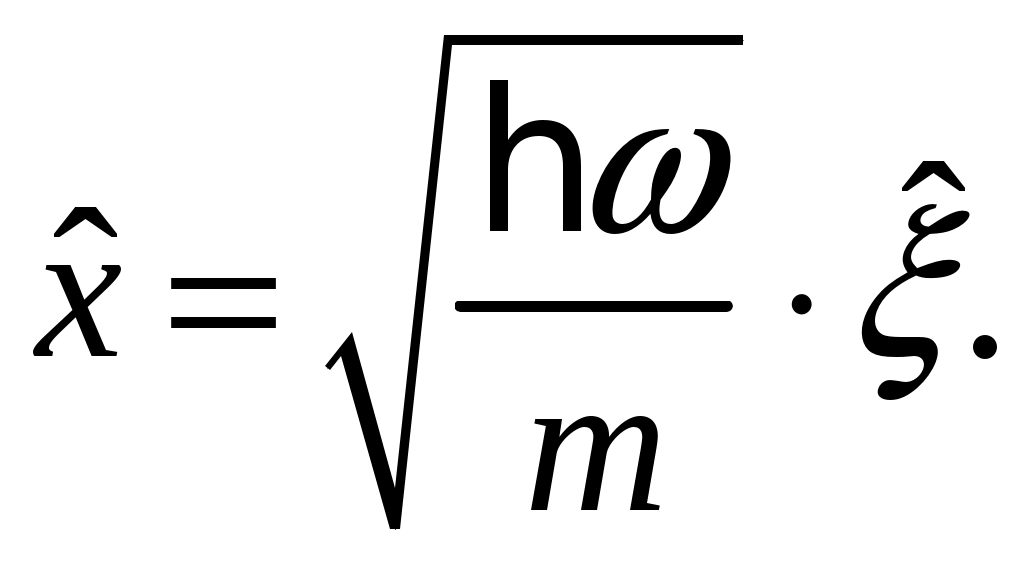, откуда

(17.4)

Гамильтониан системы будет иметь вид

(17.5)

Тогда оператор примет вид .

Запишем уравнения осциллятора для переменных и :



Они имеют следующие решения , или .

Целесообразно ввести новую переменную : . В квантовой механике ей соответствует оператор

(17.6)

Сопряжённый ему оператор имеет вид

(17.7)

Таким образом, оператор не эрмитов.

Определим перестановочные соотношения для вновь введённых переменных и и запишем гамильтониан гармонического осциллятора в этих переменных. Имеем



т.е.

(17.8)

Так как , то . Подставив полученный результат в (17.8), получим

(17.9)

Выразим и через и . Получим

(17.10)

(17.11)

и определим гамильтониан гармонического осциллятора: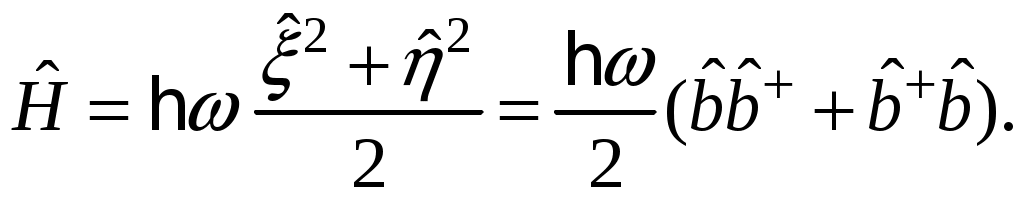



Из соотношения (17.9) следует соотношение

(17.12)

учитывая которое гамильтониан примет вид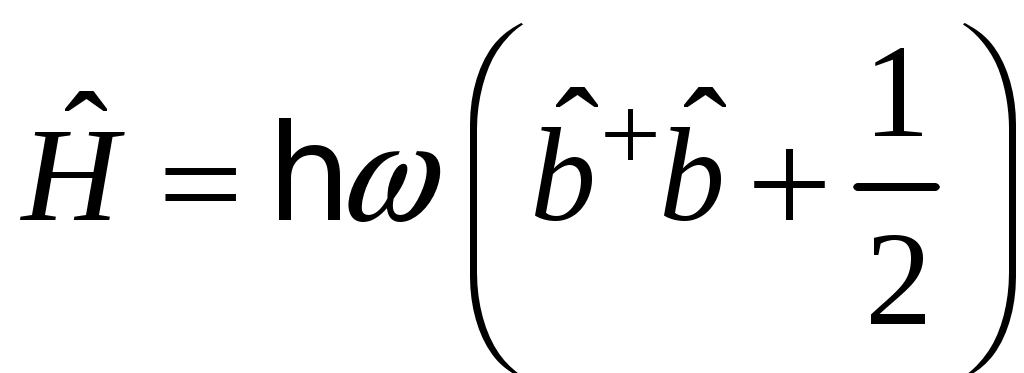



или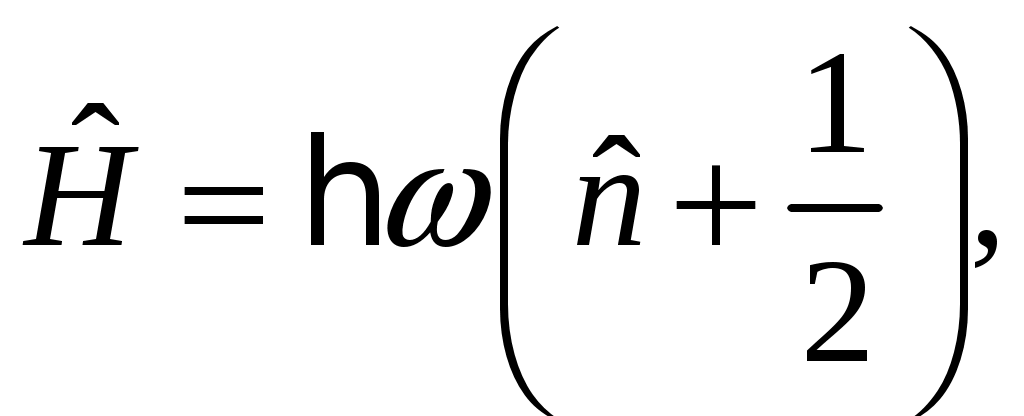

(17.13)

где оператор есть

(17.14)

Обозначим собственные значения оператора через и рассмотрим следующие уравнения на собственные функции и собственные значения:



Откуда, учитывая (17.12), получим

(17.15)

Таким образом, наша задача свелась к нахождению собственных значений оператора .

Прежде всего докажем, что не могут быть отрицательными. Для этого рассмотрим уравнение



Умножая скалярно левую и правую части равенства на и учитывая условие нормировки для векторов , получим



С другой стороны, учитывая, что



Таким образом, .

Далее установим две вспомогательные леммы.

Лемма 2. Если – собственные векторы с собственными значениями , то вектор также является собственным вектором оператора с собственным значением , т.е.

(17.16)

Доказательство. Учитывая равенства (17.12), (17.14), (17.15) запишем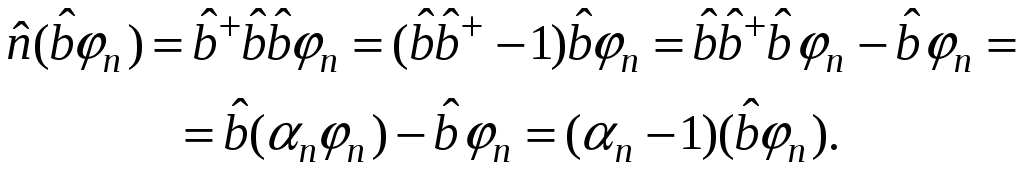



Таким образом, лемма доказана.

Лемма 3. Если – собственный вектор оператора с собственным значением , то вектор также является собственным вектором оператора с собственным значением , т.е.

(17.17)

Доказательство. Учитывая равенства (17.14), (17.12), (17.15) получим



что и требовалось доказать.

Отсюда имеем собственные векторы состояния , которым соответствует минимальное собственное значение , т.е. . Согласно Лемме 2, также является собственным вектором оператора :



но – минимальное собственное значение оператора и . Следовательно, , откуда или .

Так как собственные значения , согласно Леммам 2 и 3, отличаются друг от друга на единицу, то . Обозначим и запишем Леммы 2 и 3 с учётом введённого обозначения

(17.16`)

(17,17`)

Откуда следует, что и можно записать в следующем виде:



где и найдём из условия нормировки



Рассмотрим скалярное произведение :



С другой стороны,



Таким образом, и

(17.18)

Аналогичным образом находим , откуда

(17.19)

Таким образом, собственные значения оператора Гамильтона 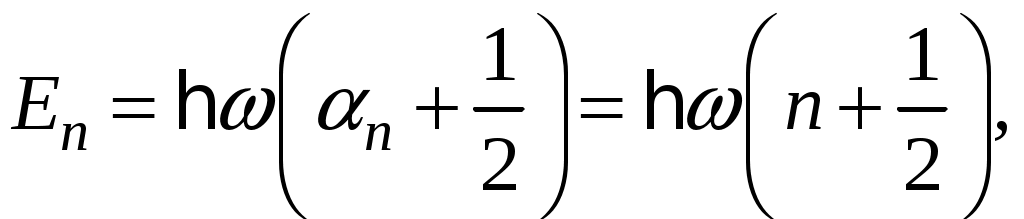принимают вид:

(17.20)

где

Из соотношения (17.20) следует, что минимальное значение энергии гармонического осциллятора отлично от нуля ( ) и спектр энергии гармонического осциллятора эквидистантен.

Применим полученный результат к примерам, приведенным в начале параграфа.

1) Электромагнитное поле эквивалентно совокупности независимых гармонических осцилляторов. Для любого такого осциллятора спектр значений энергии имеет вид



Так как осцилляторы независимы, то спектр значений энергии свободного электромагнитного поля равен сумме возможных значений энергий гармонического осциллятора: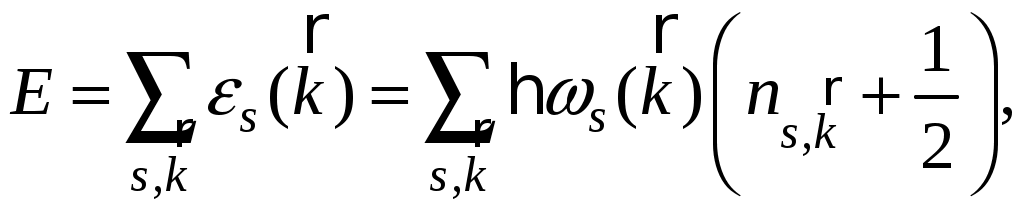

где

Выясним физический смысл оператора 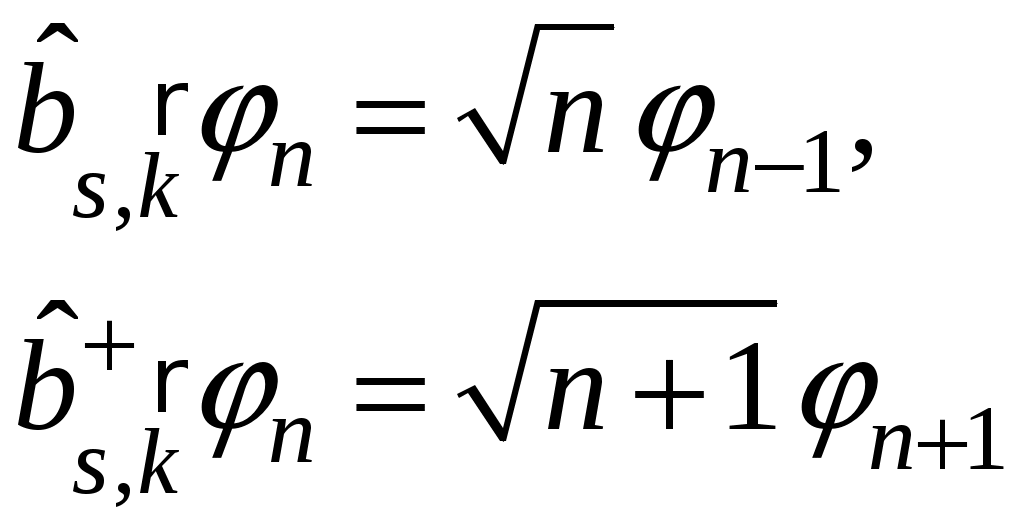. Монохроматической волне ( ) ставятся в соответствие кванты поля . Тогда в выражении для энергии приобретает смысл числа фотонов в состоянии , , при этом есть оператор числа фотонов в состоянии , . Из соотношений



следует, что есть оператор уничтожения фотона в состоянии , , а – оператор рождения фотона в состоянии , .

2) Колебания кристаллической решётки есть совокупность независимых гармонических осцилляторов. Таким образом, , где . Упругой волне в кристалле ( ) ставится в соответствие квант – фонон. Тогда – оператор числа фононов.