момент. Осциллятор и Момент Импульса. Vi. Квантовая теория гармонических колебаний и волн
 Скачать 1.55 Mb. Скачать 1.55 Mb.
|
§ 22. Спин электрона. Матрицы Паули и их свойстваОператоры спина обозначаются Спин может иметь как целые, так и полуцелые значения. В соответствие с этим выделяют два класса частиц: с целым спином – бозе-частицы и с полуцелым спином – ферми-частицы. Рассмотрим элементарный случай, когда и проекцию спина на произвольно выбранное направление, например, на ось Oz: Так как операторы спина коммутируют с операторами координаты и импульса, то полный набор физических величин с учётом спина может быть представлен двумя комбинациями: 1) 2) Представим спиновые операторы и состояния системы в матричном виде (в где где вектор 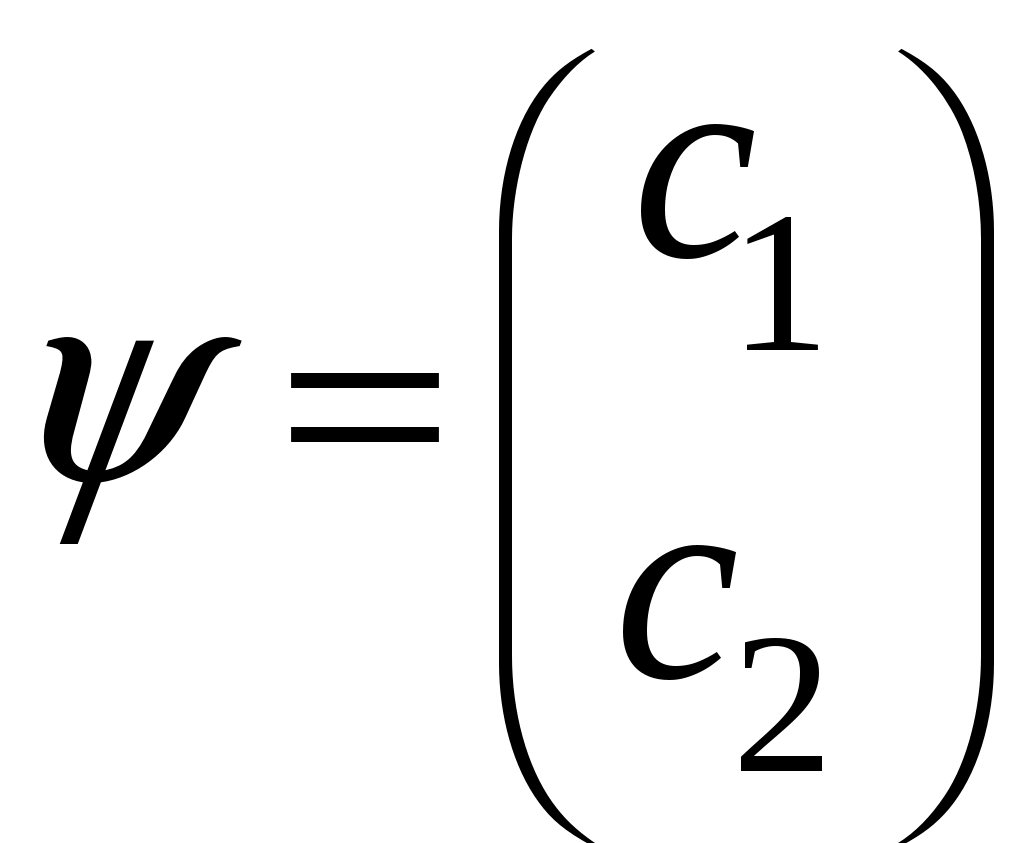 . .Найдём вид матрицы 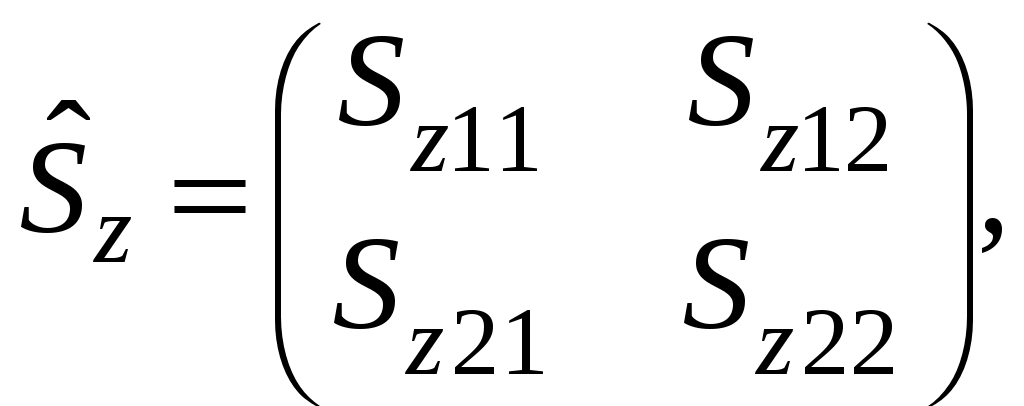 где элементы матрицы вычисляются следующим образом: Откуда 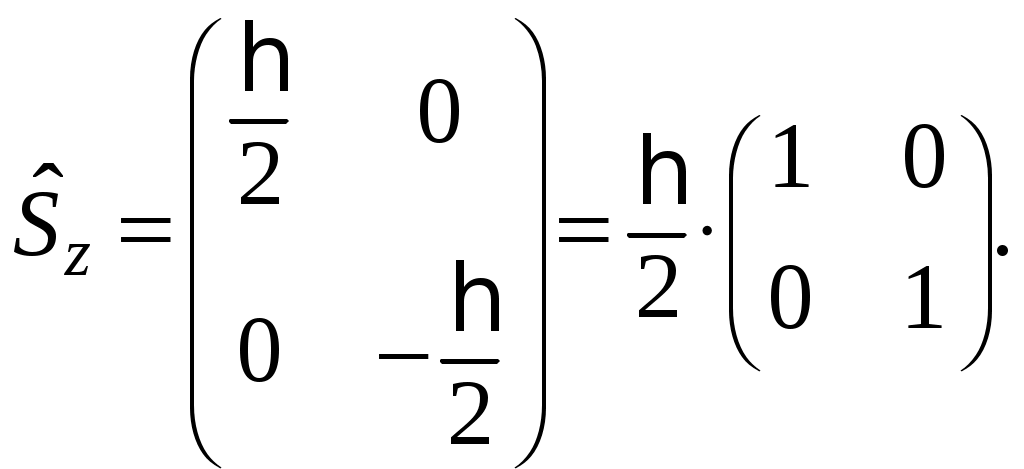 (22.6) (22.6)Для нахождения вида операторов Тогда и матрица 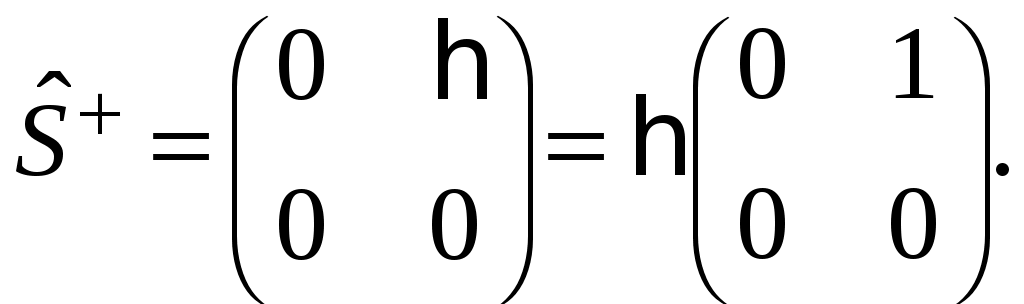 (22.7) (22.7)Матрица 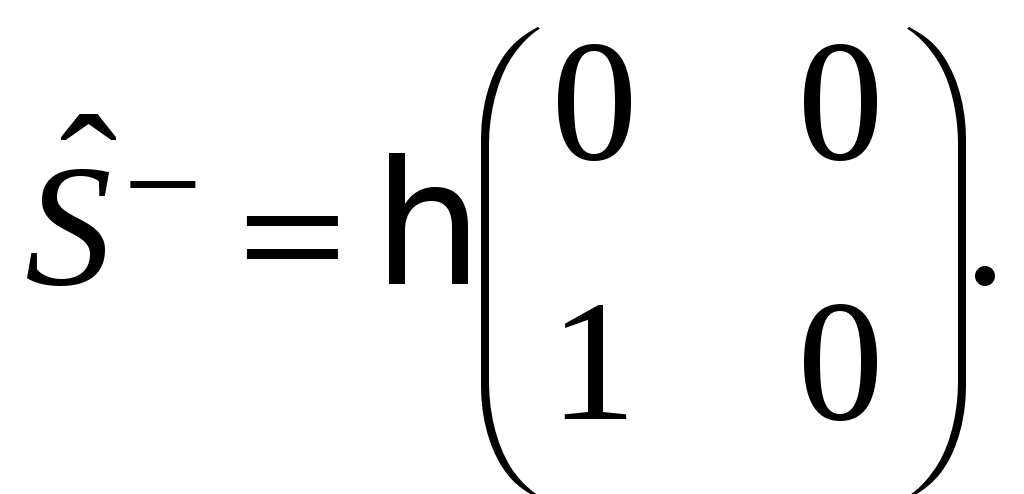 (22.8) (22.8)Операторы Откуда получаем вид операторов или 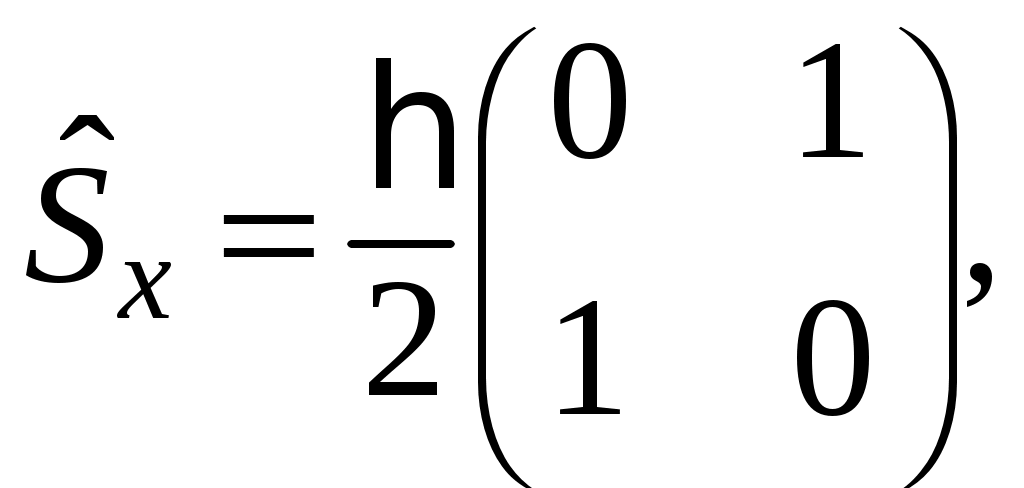 (22.9) (22.9)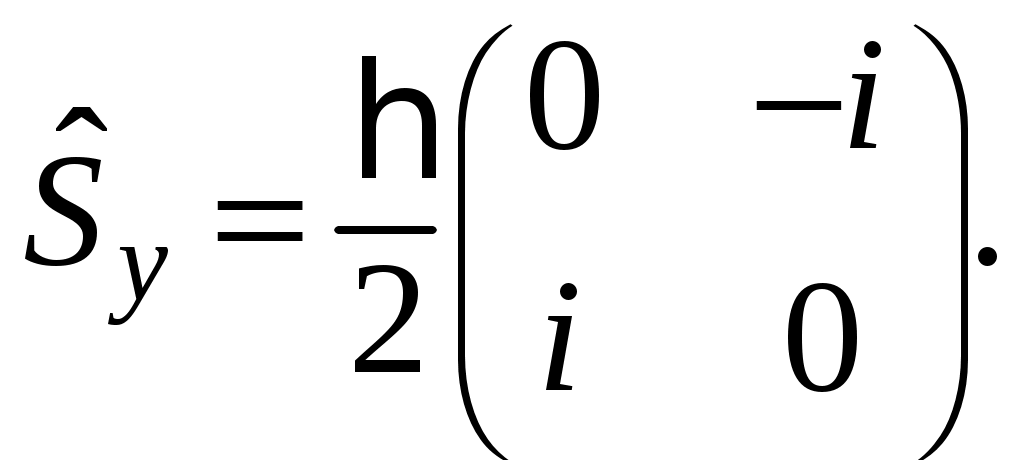 (22.10) (22.10)Таким образом, для случая где 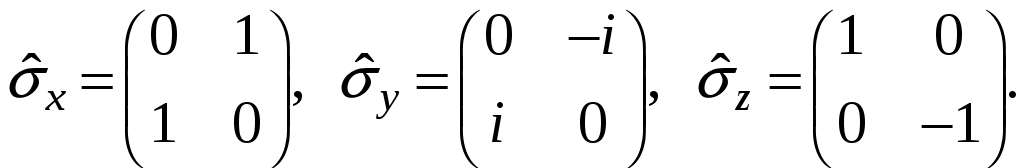 (22.12) (22.12)Матрицы Паули обладают следующими свойствами. Свойство 1. Любая двухрядная матрица может быть представлена через матрицы Паули и единичную матрицу: 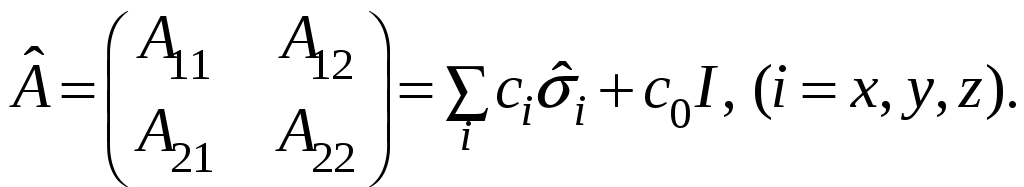 (22.13) (22.13)Свойство 2. Собственные значения любой матрицы Паули равны Найдём матричное представление собственных векторов матрицы Паули (например С одной стороны, 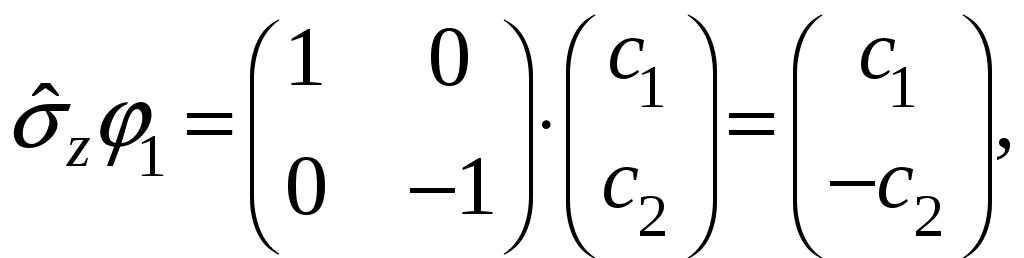 с другой – 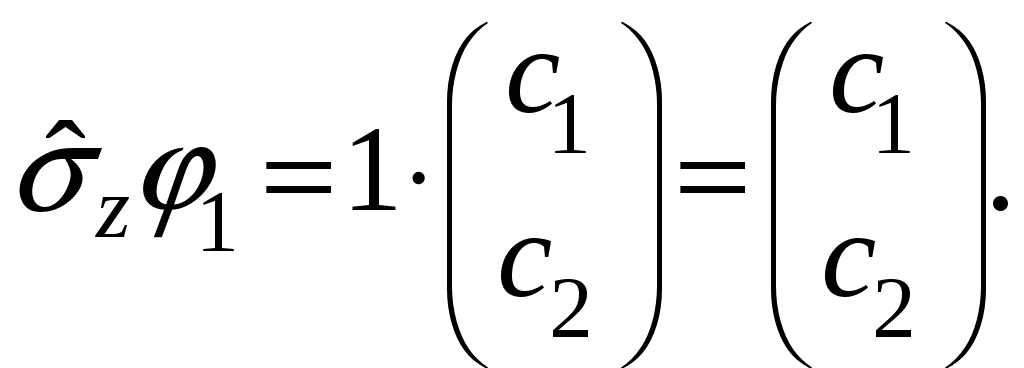 Откуда 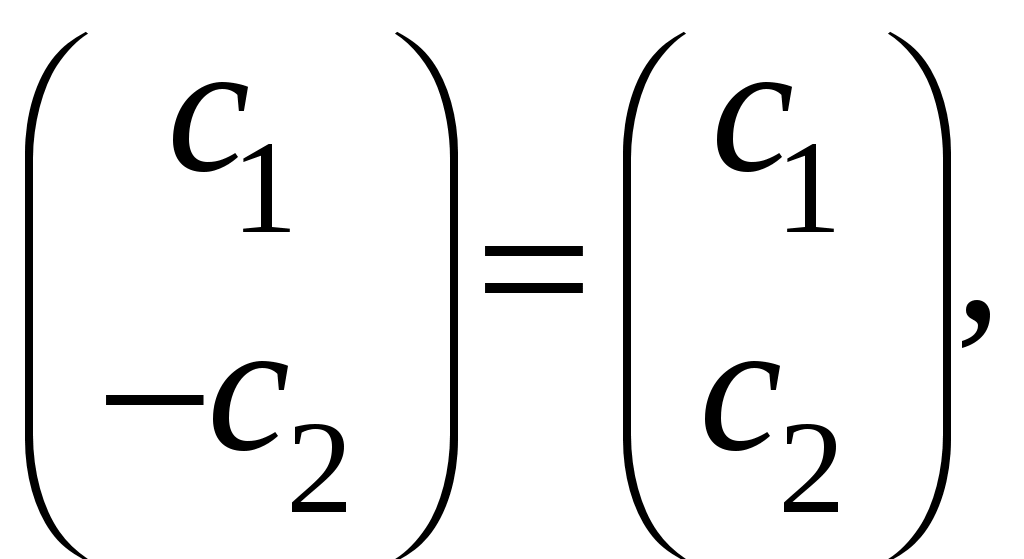 Таким образом, 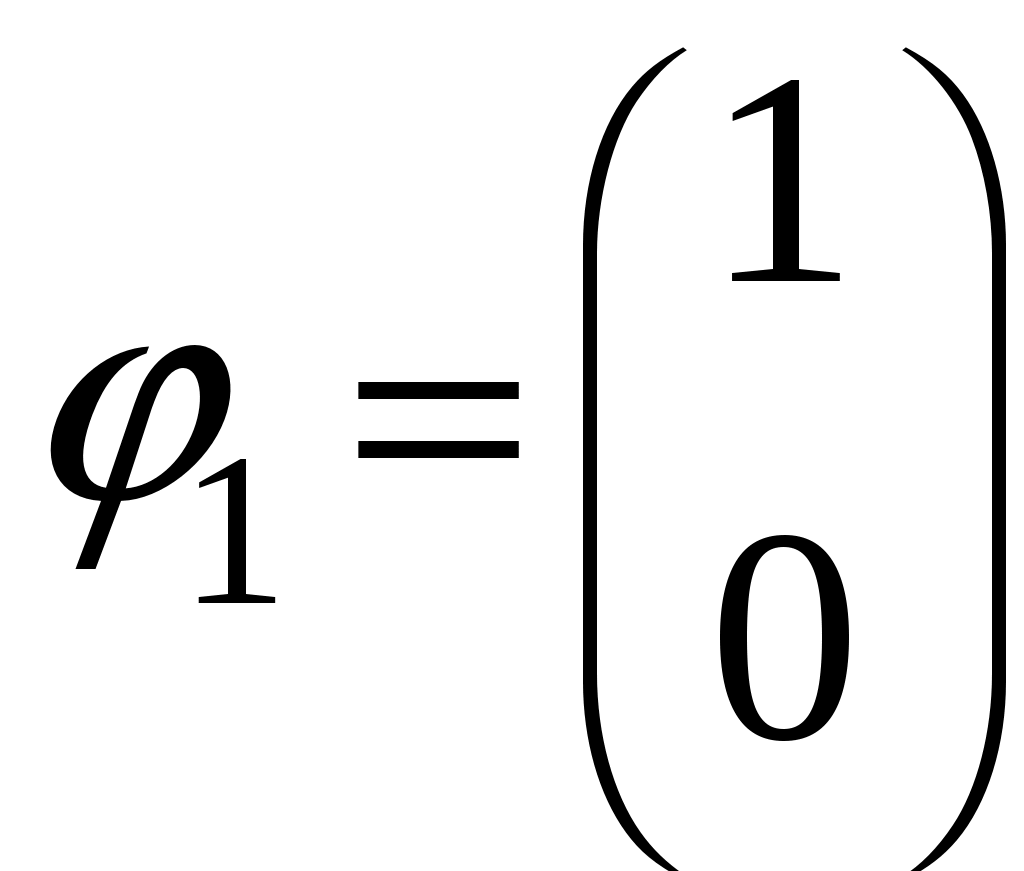 . Аналогичным образом находим . Аналогичным образом находим 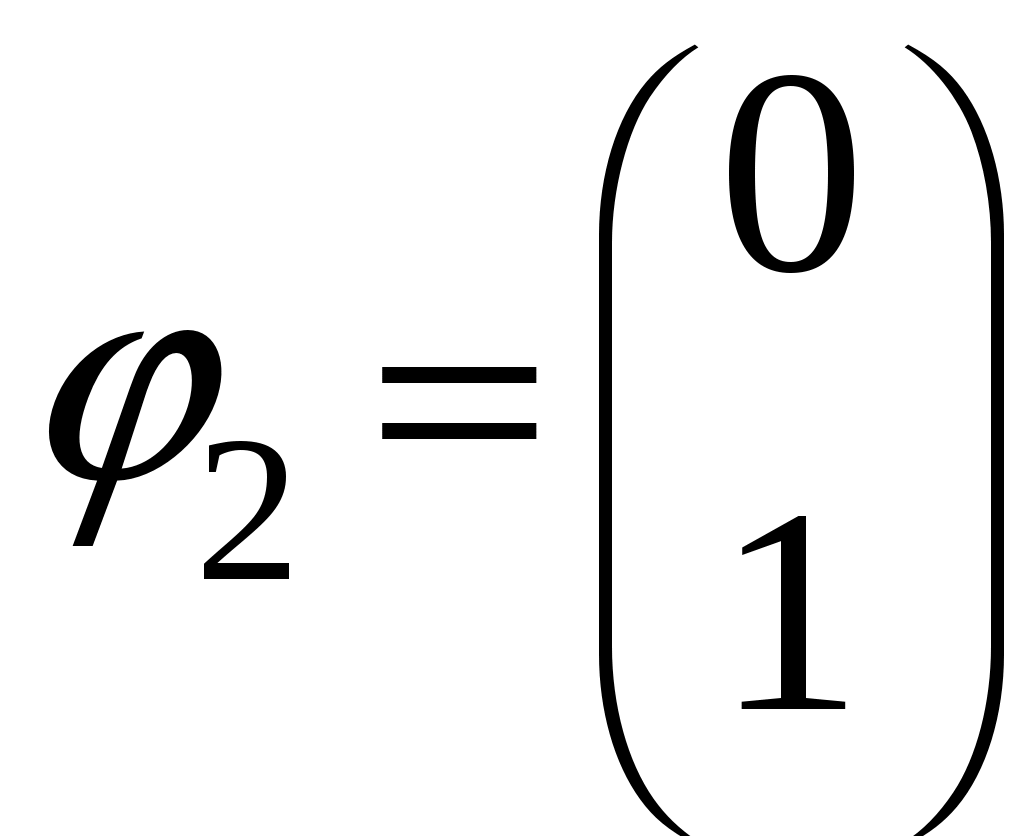 и собственные вектора операторов и собственные вектора операторов Свойство 3. Доказательство. Доказательство проведём для оператора 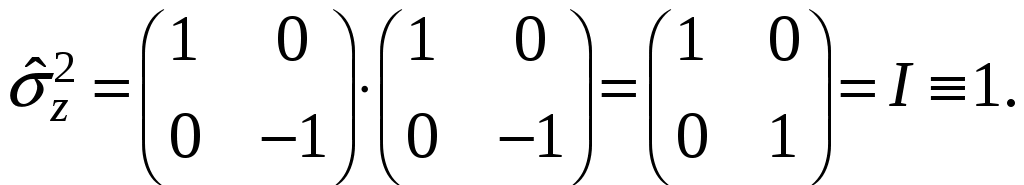 Свойство 4. Свойство 5. Доказательство. Следует из Свойства 4. С учётом спина волновая функция должна зависеть не только от пространственных переменных, но и от спиновых: Рассмотрим состояние электрона с учётом спина: 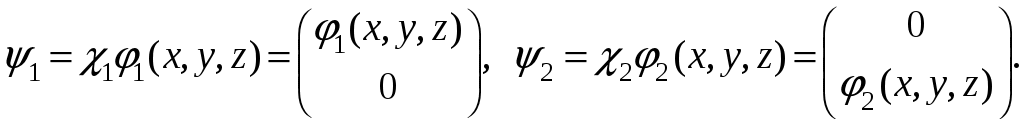 Согласно принципу суперпозиции состояний, если система может находиться в состояниях 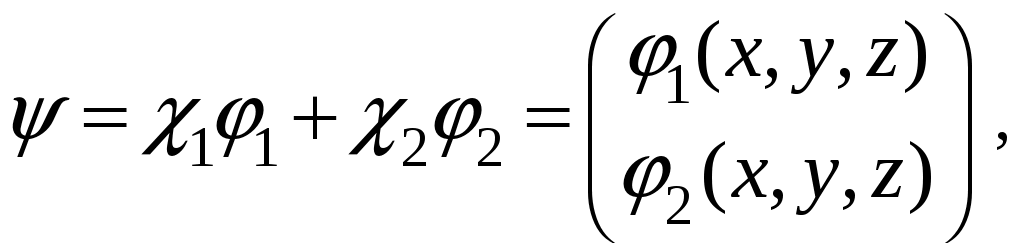 (22.17) (22.17)где |
