момент. Осциллятор и Момент Импульса. Vi. Квантовая теория гармонических колебаний и волн
 Скачать 1.55 Mb. Скачать 1.55 Mb.
|
§ 18. Стационарные состояния гармонического осциллятора. Координатное, импульсное и матричное представленияПроанализируем особенности стационарных состояний гармонического осциллятора в различных представлениях. 18.1. Координатное представлениеДля нахождения стационарных состояний гармонического осциллятора воспользуемся стационарным уравнением Шредингера Введём безразмерные переменные 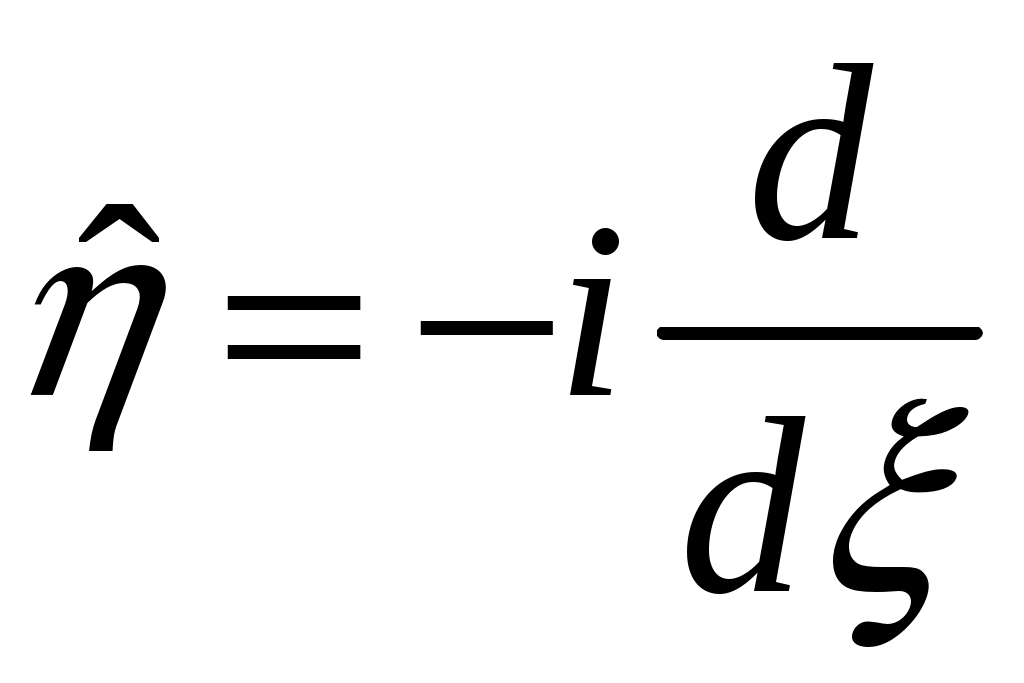 . Откуда согласно (17.6) получим . Откуда согласно (17.6) получим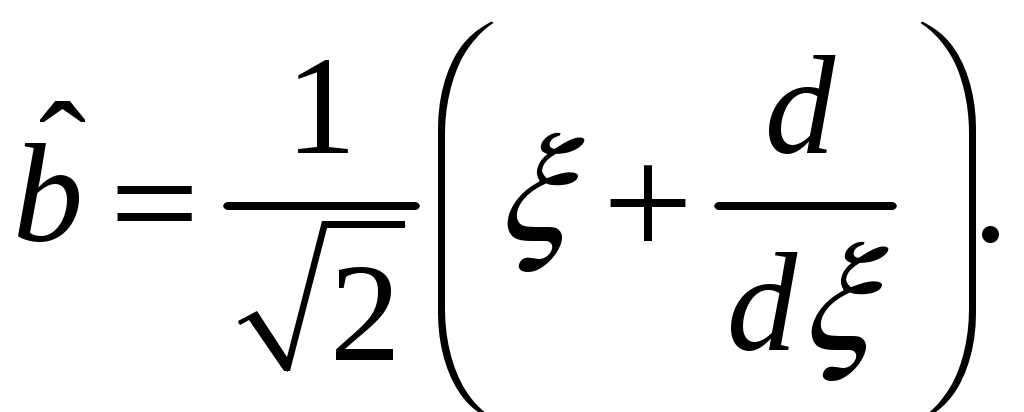 (18.1) (18.1)Используя равенство (17.19), найдём  Аналогично Определим вид собственной функции 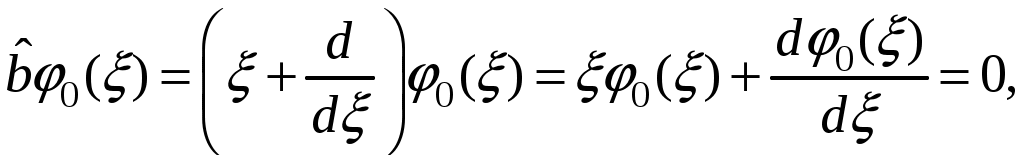 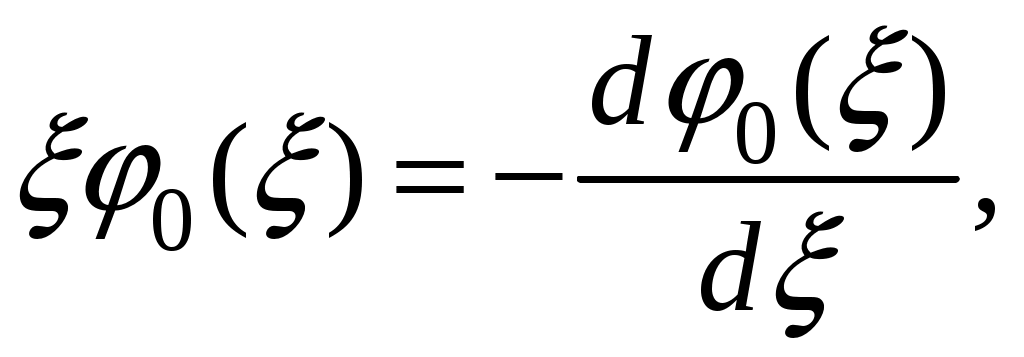 что дает Постоянную  Откуда 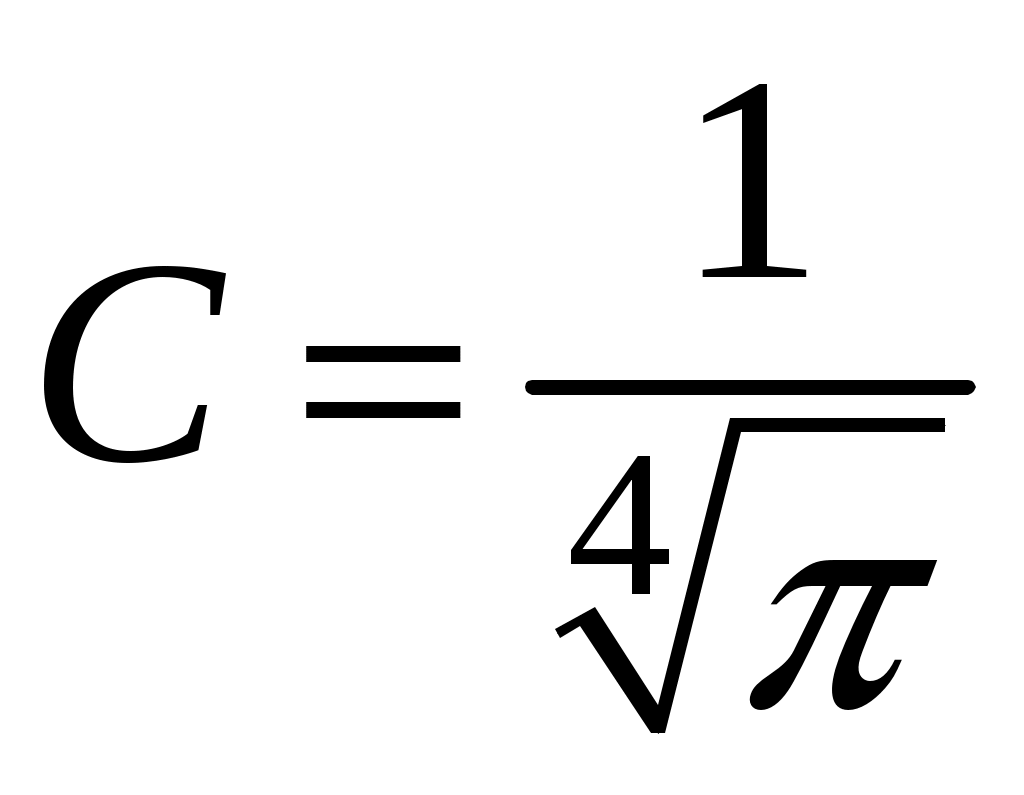 и согласно выражению (18.3) 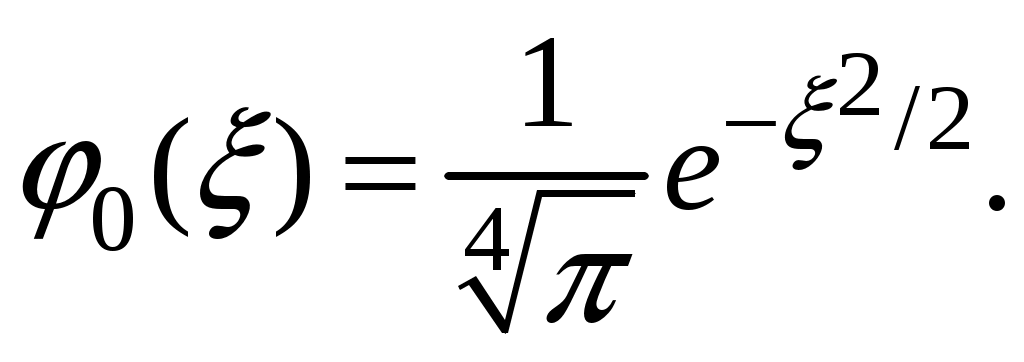 (18.4) (18.4)Воспользуемся соотношением (18.1) для нахождения вектора  т.е.  (18.5) (18.5)где 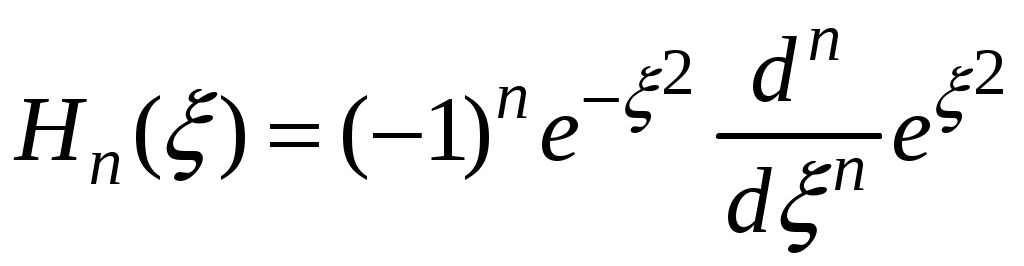 (18.6) (18.6)или в развёрнутом виде 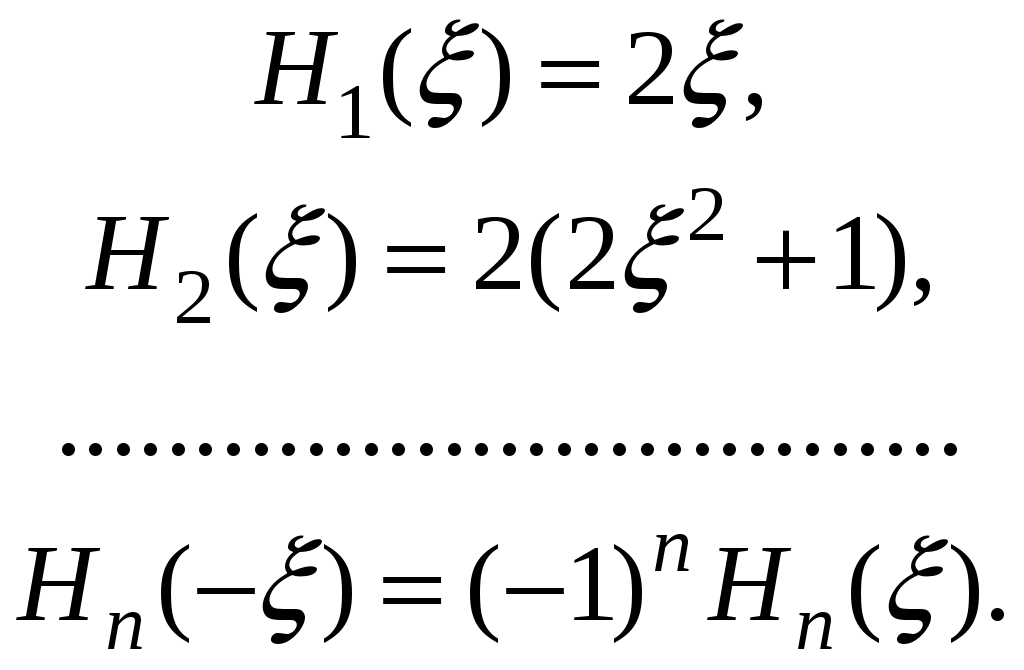 (18.6`) (18.6`)Из последних соотношений очевидно, что состояния гармонического осциллятора могут быть как чётными, так и нечётными. 18.2. Импульсное представлениеПо аналогии с выше рассмотренным представлением определим операторы 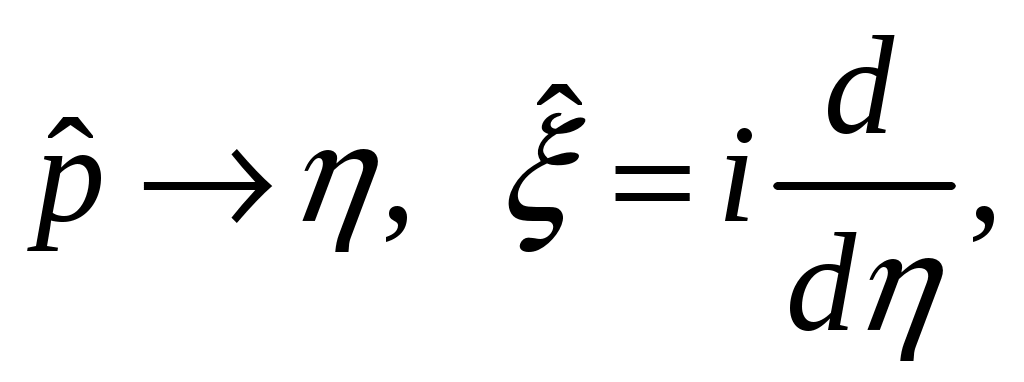 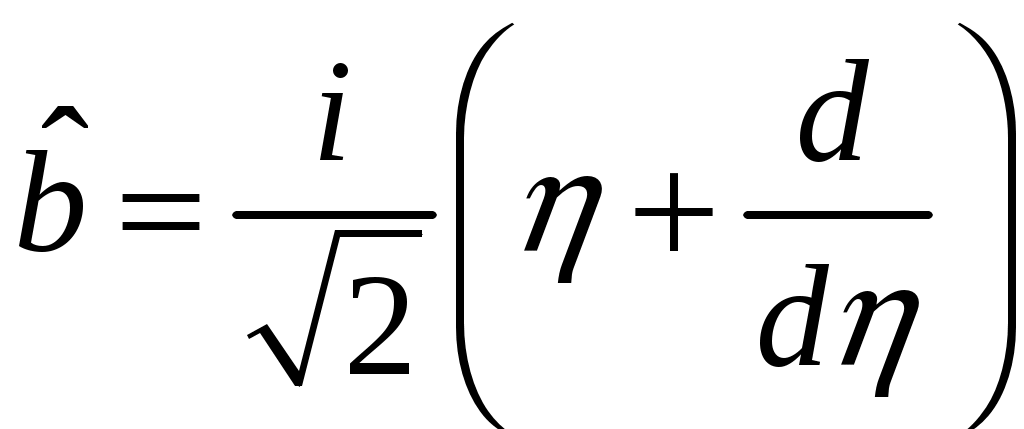 . (18.7) . (18.7)После чего получим следующие выражения для волновых функций стационарных состояний гармонического осциллятора в импульсном представлении: 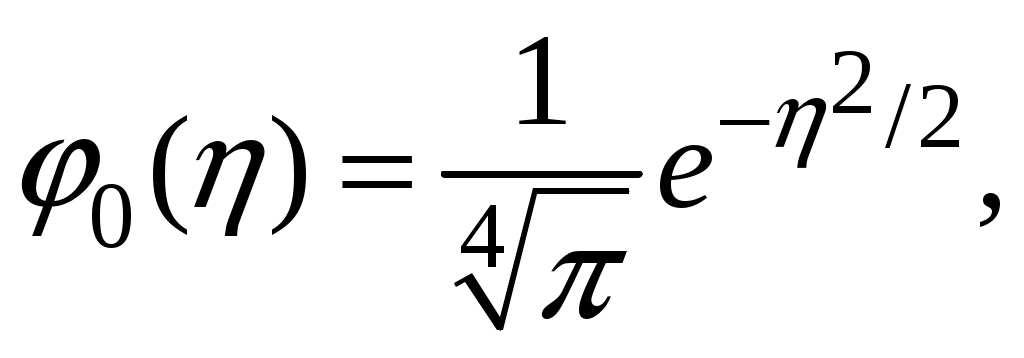  (18.8) (18.8)18.3. Матричное представлениеСогласно (17.4) и (17.10) 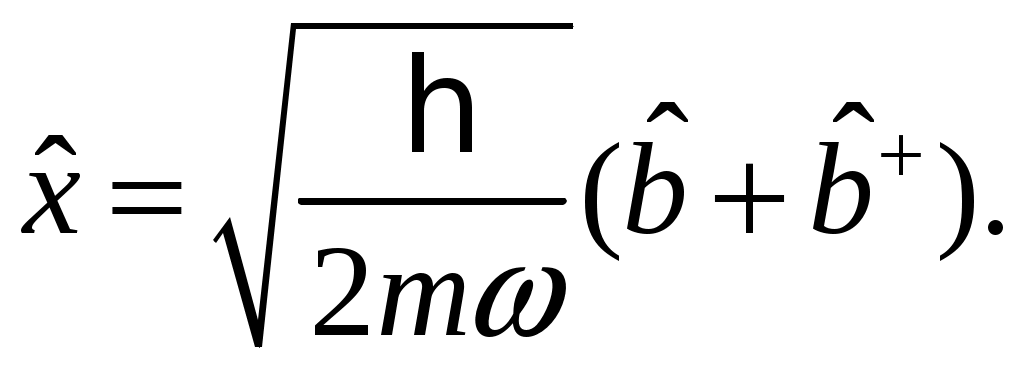 (18.9) (18.9)Найдём матричные элементы оператора Откуда получим Найдём минимальное значение Таким образом, матрица оператора b примет вид:  (18.10) (18.10)Матрица 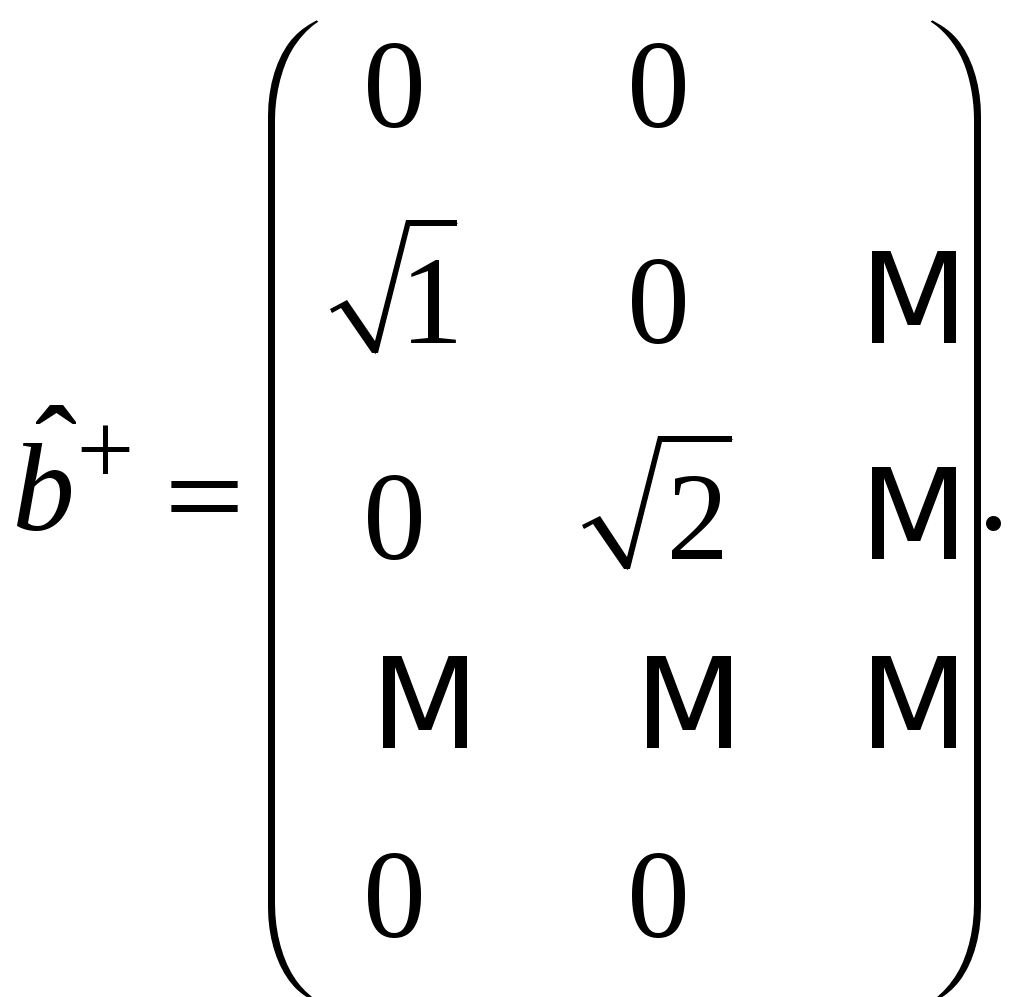 (18.11) (18.11)Подставляя (18.10) и (18.11) в (18.9) находим вид оператора координаты в матричном представлении: 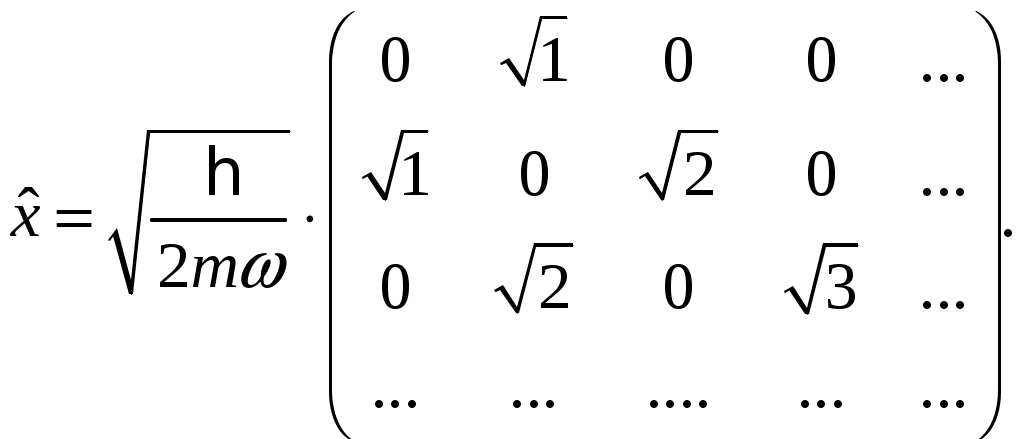 (18.12) (18.12)Используя соотношения (17.3), (17.11), можно получить оператор импульса в матричном представлении. Глава VII. Квантовая теория моментаНаряду с энергией и импульсом момент количества движения относится к фундаментальным физическим величинам, связанным с наиболее общими свойствами пространства-времени. Из однородности пространства-времени следует сохранение энергии-импульса для замкнутой системы. Изотропность пространства (симметрия относительно вращения) приводит к сохранению момента количества движения. В квантовой механике моменту количества движения отводится особое место в силу его специфических квантовых свойств. |
