момент. Осциллятор и Момент Импульса. Vi. Квантовая теория гармонических колебаний и волн

• Название: Vi. Квантовая теория гармонических колебаний и волн
• Анкор: момент
• Дата: 15.12.2021
• Размер: 1.55 Mb.
• Имя файла: Осциллятор и Момент Импульса.doc
• Тип: Закон; #304460
• страница: 7 из 7

§ 24. Уравнение Паули. Собственный магнитный момент электрона

Основным уравнением нерелятивистской квантовой механики является уравнение Шредингера, описывающее движение нерелятивистской частицы без учета спина:



где – оператор Гамильтона. Теория Шредингера исходила из предположения, что электрон обладает лишь степенями свободы, которые соответствуют движению материальной точки в пространстве координат , , .

Введение новой степени свободы, связанной со спином, дает новые возможности для перехода от величин классической механики к квантовым операторам и позволяет построить оператор

(24.1)

где – матрицы Паули, а – импульс частицы. Оператор (24.1) может быть использован при построении оператора энергии.

Произвольное состояние электрона при учете спина записывается в виде двухрядной матрицы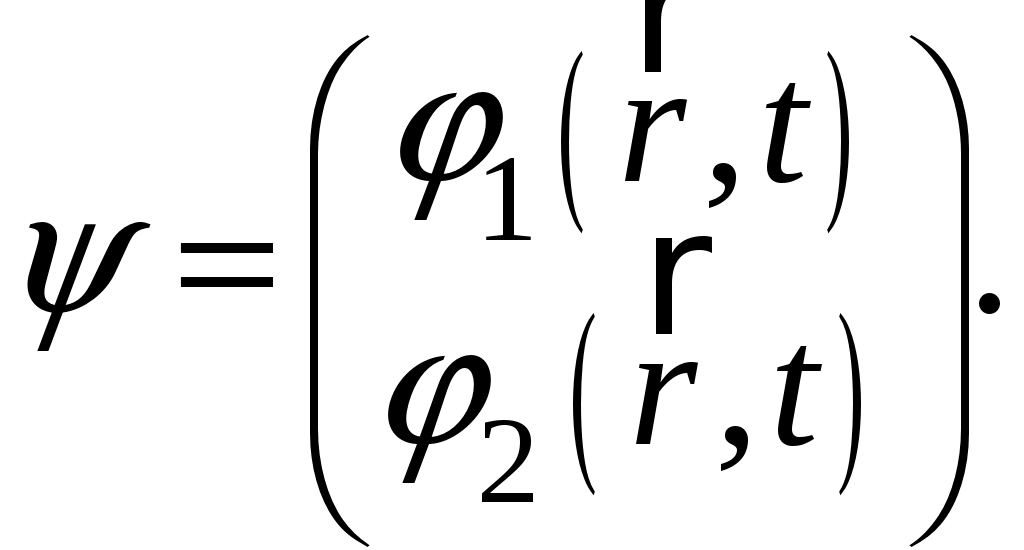



Вследствие этого гамильтониан должен быть двухрядной матрицей и, согласно свойствам матриц Паули, может быть представлен через матрицы Паули и единичную матрицу .

Гамильтониан не должен зависеть от направлений, т.е. пространственные переменные должны входить в гамильтониан равноправным образом, и в то же время он должен включать в себя матрицы Паули . Таким образом, из соображений размерности можно положить, что гамильтониан свободной частицы с учетом спина имеет вид

(24.2)

Используя свойства матриц , , , а именно,



и коммутативность операторов , ,



вычислим квадрат скалярного произведения :



Откуда



Как и следовало ожидать, в отсутствие внешних полей наличие спина никоим образом не проявляется, и введение оператора, определяемого формулой (24.1), здесь ничего не вносит.

Иначе обстоит дело при наличии магнитного поля, когда классическая функция Гамильтона электрона в электромагнитном поле с векторным потенциалом 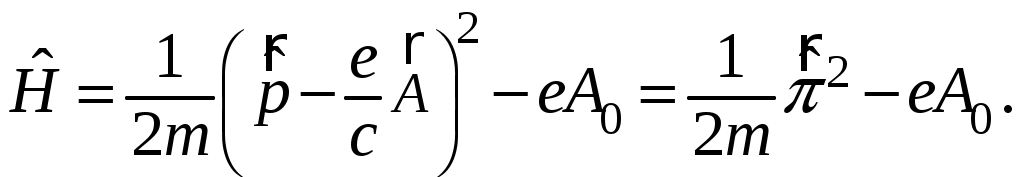и скалярным потенциалом имеет вид



Согласно правилам квантования



учитывая наличие спина у электрона



оператор Гамильтона примет вид

(24.3)

Рассмотрим квадрат скалярного произведения операторов и :



Используя свойства матриц Паули, получим



Учитывая выражения, справедливые для



квадрат скалярного произведения примет вид

(24.4)

В данном случае операторы 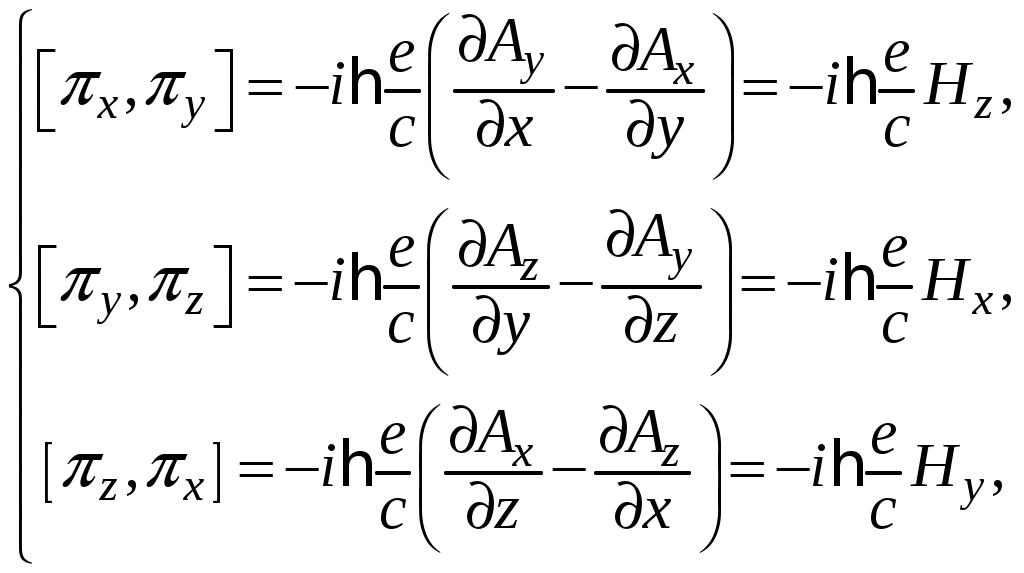, , не коммутативны, а удовлетворяют перестановочным соотношениям

(24.5)

где , , – составляющие магнитного поля.

Оператор Гамильтона (24.3) с учетом (24.4), (24.5) примет вид

(24.6)

или

(24.7)

где постоянная есть магнитный момент электрона. Таким образом, наличие спина у электрона влечет за собой наличие собственного магнитного момента электрона.

Определив выражение оператора Гамильтона (24.7), запишем волновое уравнение, называемое уравнением Паули, которое описывает состояние электрона в магнитном поле без поправки на теорию относительности: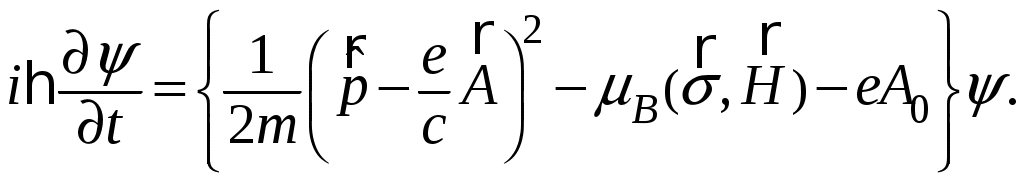

(24.8)

Список литературы

1. 
   Давыдов А.С. Квантовая механика. 2-е изд. – М.: Наука, 1973. – 704 с.
   
2. 
   Блохинцев Д.И. Основы квантовой механики. 5-е изд. – М.: Наука, 1976. – 664 с.
   
3. 
   Ландау Л.Д., Лифшиц Е.М. Квантовая механика (Нерелятивистская теория). 4-е изд., испр. – М.: Наука, 1989. – 768 с.
   
4. 
   Мессиа А. Квантовая механика. Том 1. – М.: Наука, 1978. – 480 с.
   
5. 
   Бом Д. Квантовая теория. 2-е изд. – М.: Наука, 1965. – 731 с.