момент. Осциллятор и Момент Импульса. Vi. Квантовая теория гармонических колебаний и волн

• Название: Vi. Квантовая теория гармонических колебаний и волн
• Анкор: момент
• Дата: 15.12.2021
• Размер: 1.55 Mb.
• Имя файла: Осциллятор и Момент Импульса.doc
• Тип: Закон; #304460
• страница: 3 из 7

§ 19. Общие свойства и особенности квантового момента

При построении квантовой теории момента количества движения воспользуемся принципом соответствия, согласно которому каждой физической величине ставится в соответствие линейный эрмитов оператор



Следовательно, соотношения между физическими величинами в классической теории должны перейти в соотношения между операторами физических величин в квантовой механике. В частности, классическим скобкам Пуассона

(19.1)

ставятся в соответствие квантовые скобки :

(19.2)

Это своеобразное применение принципа соответствия между классической и квантовой механиками оказалось очень плодотворным.

Учитывая выражение момента импульса



с помощью (19.1) можно получить следующие классические соотношения:





Откуда, согласно принципу соответствия, сопоставив классическим скобкам Пуассона квантовые, получаем следующие соотношения для квантово-механического момента импульса :





т.е. согласно (19.2)

(19.3)

(19.4)

Из соотношений (19.3) и (19.4) следует, что одновременно измеримыми величинами являются квадрат момента и одна из его проекций. В качестве последней примем :



Геометрически это можно представить с помощью так называемого «конуса состояния».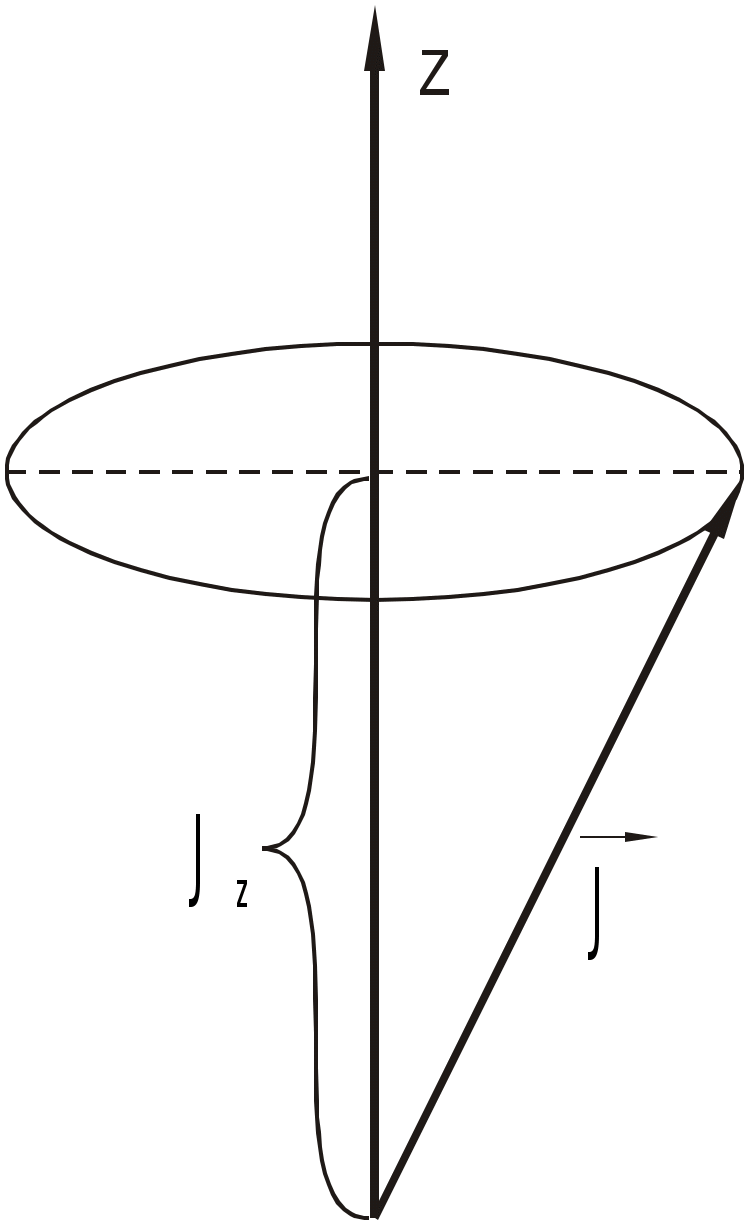



Одновременно точные значения могут иметь лишь величины и .

§ 20. Собственные значения и собственные векторы проекции и квадрата момента

Основная задача квантовой теории момента заключается в определении общих собственных векторов и собственных значений проекции и квадрата момента. Из одновременной измеримости и следует, что соответствующие операторы этих величин имеют общую систему собственных функций :

(20.1)

(20.2)

Рассмотрим некоторые свойства оператора момента количества движения.

Свойство 1. При фиксированном значении квадрата момента количества движения проекция момента принимает значения из интервала:

(20.3)

Доказательство. Для доказательства этого свойства воспользуемся определением:



Подействуем оператором квадрата момента на вектор состояния :



Умножая последнее выражение на и интегрируя по всей области изменения переменных, получим



Тогда, учитывая, что средние значения не отрицательны, приходим к выводу



т.е. максимальная проекция момента не превосходит длины вектора момента количества движения:



что и требовалось доказать.

Свойство 2. Если – собственный вектор оператора квадрата момента с собственным значением , то и также собственные вектора оператора квадрата момента с тем же собственным значением , т.е.

(20.4)

(20.5)

Доказательство. Подействуем оператором на вектор состояния и воспользуемся свойством (19.4):





Аналогично проводится доказательство для вектора .

Таким образом, из коммутируемости операторов проекций и с оператором квадрата момента импульса следует, что их действие на вектор состояния не меняет .

Вместо операторов , удобно перейти к их комплексным комбинациям:

(20.6)

(20.7)

Выразим имеющиеся соотношения через введенные комплексные операторы. Для этого найдем коммутатор :



Для дальнейших вычислений воспользуемся свойством коммутатора:



Тогда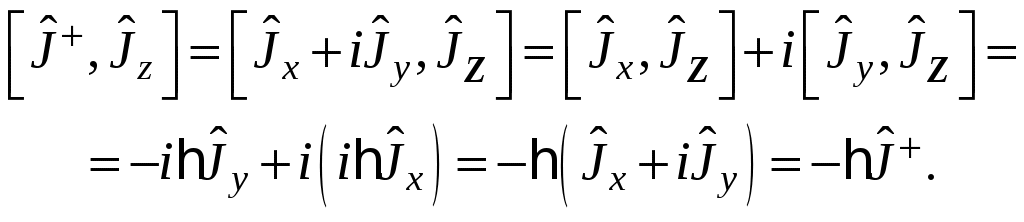

(20.8)

Можно показать, что

(20.9)

Аналогично проводятся вычисления для :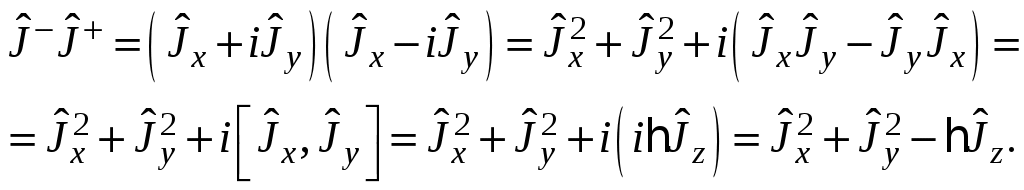

(20.10)

(20.11)

(20.12)

Откуда, учитывая определение квадрата момента , следует, что

(20.13)

или

(20.14)

Для решения задачи о нахождении спектра собственных значений операторов и рассмотрим несколько вспомогательных лемм.

Лемма 4. Если – собственный вектор оператора с собственным значением , то вектор – собственный вектор оператора с собственным значением , т.е.



Доказательство. Подействуем оператором 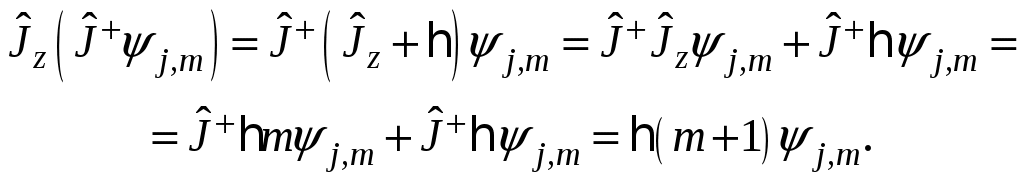на вектор . С учетом равенств (20.9) и (20.1) получаем:



Что и требовалось доказать.

Лемма 5. Если – собственный вектор оператора с собственным значением , то тоже есть собственный вектор с собственным значением , т.е.



Доказательство. Проводится аналогично с учетом (20.11) и (20.1).

Из рассмотренных вспомогательных лемм в дальнейшем нам понадобятся два следствия:

1. 
   (20.15)
   
2. 
   (20.16)
   

где , – некоторые постоянные.

Данные леммы и их следствия помогают ответить на вопрос о спектре собственных значений проекции момента, если нам известно хотя бы одно значение. Согласно леммам 4 и 5 собственные значения проекции момента количества движения , которым принадлежат собственные функции , , , отличаются на единицу и находятся, согласно доказанной теореме, в интервале . Таким образом, при фиксированном значении значения ограничены сверху и снизу. Пусть и соответственно наименьшее и наибольшее значения при заданном , т.е. . Тогда

(20.17)

(20.18)

С учетом равенств (20.17), (20.14) и (20.18), (20.1) можно записать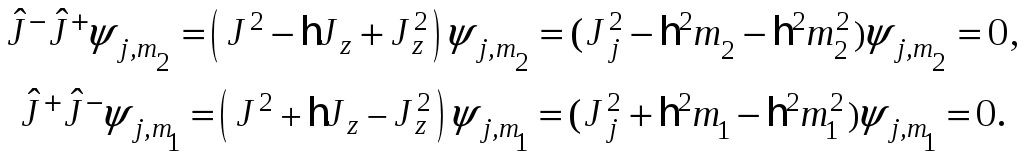



Откуда следует, что



Так как по условию , то , откуда

(20.19)

Определим значения постоянных и в выражениях (20.15), (20.16). Для этого применим условие нормировки



С другой стороны,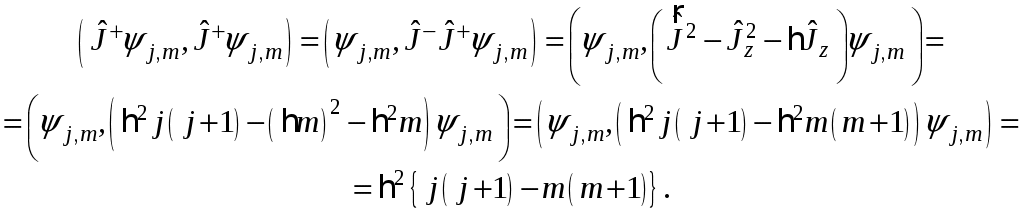



Сравнивая полученные выражения, делаем вывод, что

(20.20)

(20.21)

Согласно (20.15), (20.16), (20.20), (20.21):

(20.22)

(20.23)