задачи линейного и нелинейного программирования. Задачи ЛП и НП. Задачи линейного программирования
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
Задачи линейного программирования Решить графическим методом задачу линейного программирования. F(x) = 2x1 + 3x2 min 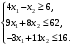 x1 0, x2 0. Решение: Геометрический (графический) метод решения задачи линейного программирования состоит в следующем. Строится допустимый многоугольник решений системы неравенств. Сначала в декартовой системе координат строим прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств: 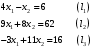 Каждое ограничение-неравенство определяет координатную полуплоскость. В зависимости от знака неравенств стрелок укажем требуемые полуплоскости. Для построения прямой 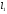 из уравнения выразим из уравнения выразим 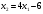 . . Прямая 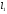 делит плоскость на две полуплоскости, в одной из которых справедливо неравенство делит плоскость на две полуплоскости, в одной из которых справедливо неравенство 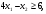 а в другой – противоположное ему. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. а в другой – противоположное ему. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. Для того чтобы проверить, какая из полуплоскостей состоит из решений неравенства 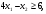 следует взять точку из какой-либо полуплоскости и проверить, выполняется ли это равенство в этой точке. Возьмем точку с координатами х1=0, х2=0. Неравенство следует взять точку из какой-либо полуплоскости и проверить, выполняется ли это равенство в этой точке. Возьмем точку с координатами х1=0, х2=0. Неравенство 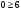 неверное, поэтому данная точка лежит не в той полуплоскости (рис. 1.1). неверное, поэтому данная точка лежит не в той полуплоскости (рис. 1.1).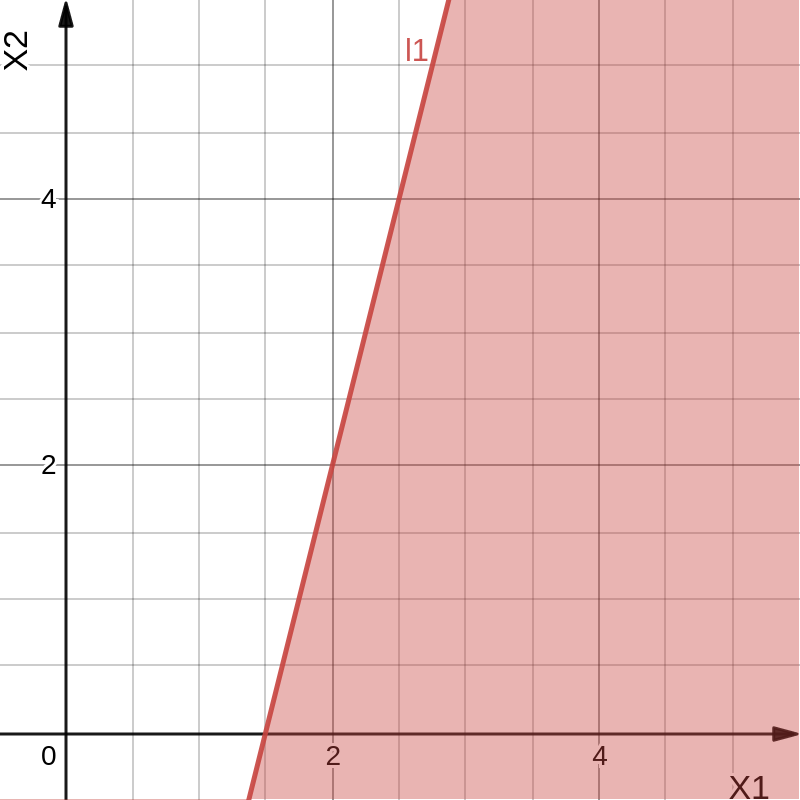 Рис. 1.1. Нахождение нужной полуплоскости Аналогично строим остальные прямые. Множество точек на плоскости, удовлетворяющих системе ограничений, составляет некоторую выпуклую многоугольную область. Условия неотрицательности переменных X1 0 и X2 0 приводят к тому, что эта область находится в первой координатной четверти. В результате пересечения всех полуплоскостей находим неограниченный многоугольник решений - треугольник ABС (рис. 1.2). 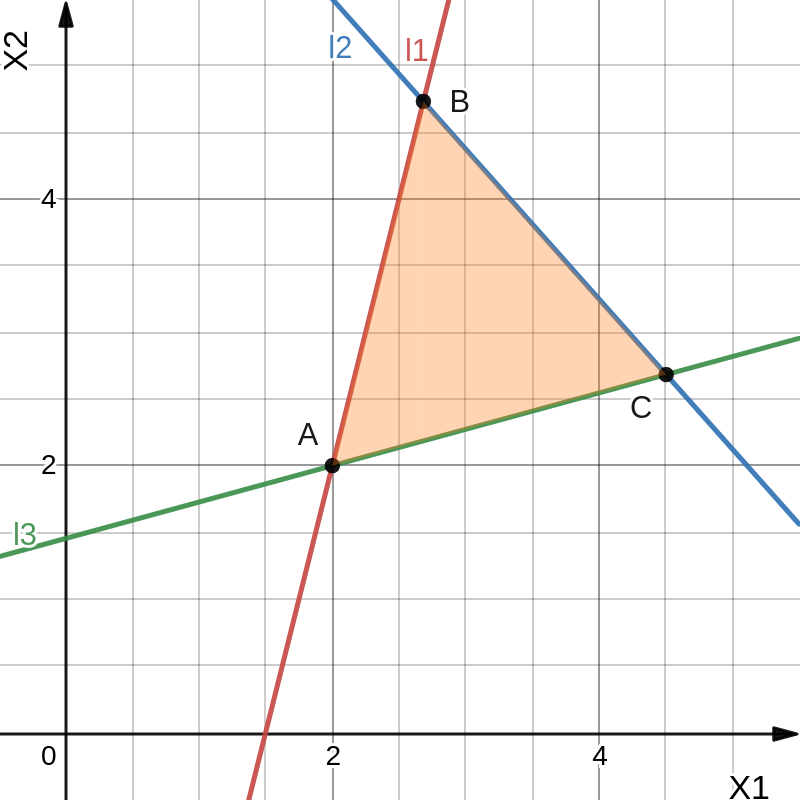 Рис. 1.2. Построение многоугольника решений Построим линию уровня целевой функции F(x) = 2x1 + 3x2, и градиент целевой функции 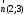 . . Передвигая линию уровня вдоль градиента параллельно самой себе, находим точки экстремума. Точкой минимума будет точка первого касания линии уровня с допустимым многоугольником (рис.1.3). 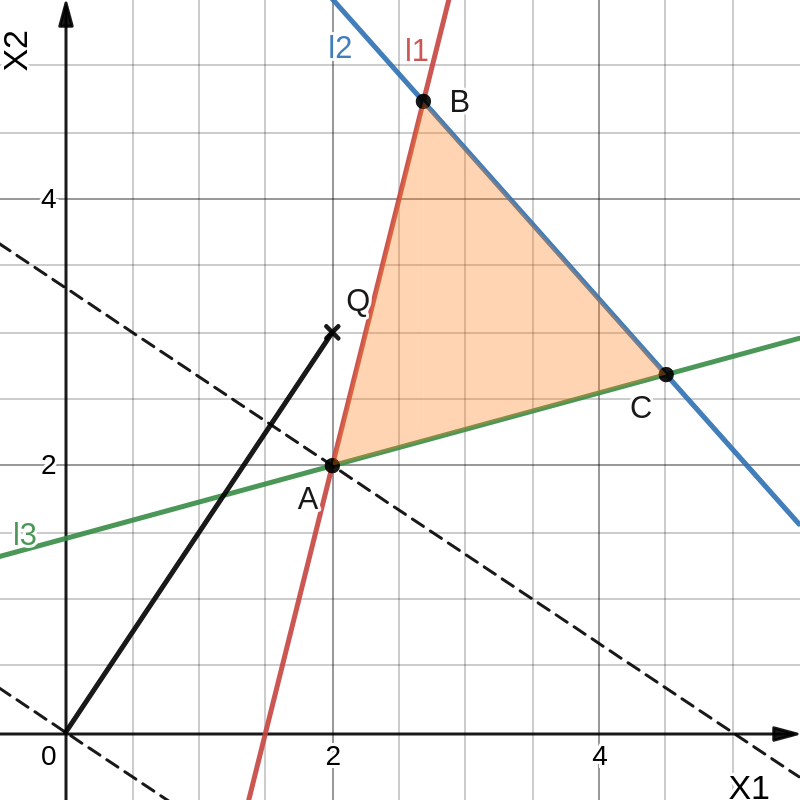 Рис.1. 3. Линия уровня целевой функции. Минимум целевой функции достигается в точке А. Найдем ее координаты: 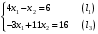 Решая систему линейных уравнений, находим координаты точки А (2;2). Значение целевой функции в точке А: Fmin=F(А) = 4+ 6=10 Точкой максимума – точка отрыва линии уровня от допустимого многоугольника. В нашем это точка В. Решить задачу симплекс-методом F(x) = x1 + 3x2 + 3x3 max 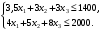 x1 0, x2 0, x3 0. Решение: Решим данную задачу симплекс-методом. Введем дополнительные переменные х4, х5 для приведения задачи к каноническому виду. Перепишем ограничения в каноническом виде: 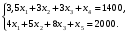 Решим систему уравнений относительно базисных переменных: x4, x5 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,1400,2000) Составим симплекс-таблицу
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. Определение новой базисной переменной: В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю. Определение новой свободной переменной: Вычислим значения Di по строкам как частное от деления: bi / ai3 и из них выберем наименьшее: min (1400 : 4,2; 2000 : 8 ) = 250 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (8) и находится на пересечении ведущего столбца и ведущей строки
Вместо переменной x5 в план 1 войдет переменная x3. Строка, соответствующая переменной x3, получена в результате деления всех элементов строки x5 предыдущего плана на разрешающий элемент 8. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Таким образом, в новом плане заполнены строка x3 и столбец x3. Все остальные элементы нового плана, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент. Получаем новую симплекс-таблицу:
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (350 : 43/8 , 250 : 5/8 ) = 80 Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен (43/8) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x4 в план 2 войдет переменная x2. Строка, соответствующая переменной x2 в плане 2, получена в результате деления всех элементов строки x4 плана 1 на разрешающий элемент 43/8. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Таким образом, в новом плане заполнены строка x2 и столбец x2. Все остальные элементы нового плана, включая элементы индексной строки, определяются по правилу прямоугольника. Получаем новую симплекс-таблицу:
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Оптимальный план можно записать так: x1 = 0, x2 = 80, x3 = 200 F(X) = 1*0 + 3*80 + 3*200 = 840 Проверка решения с помощью надстройки Поиск решения 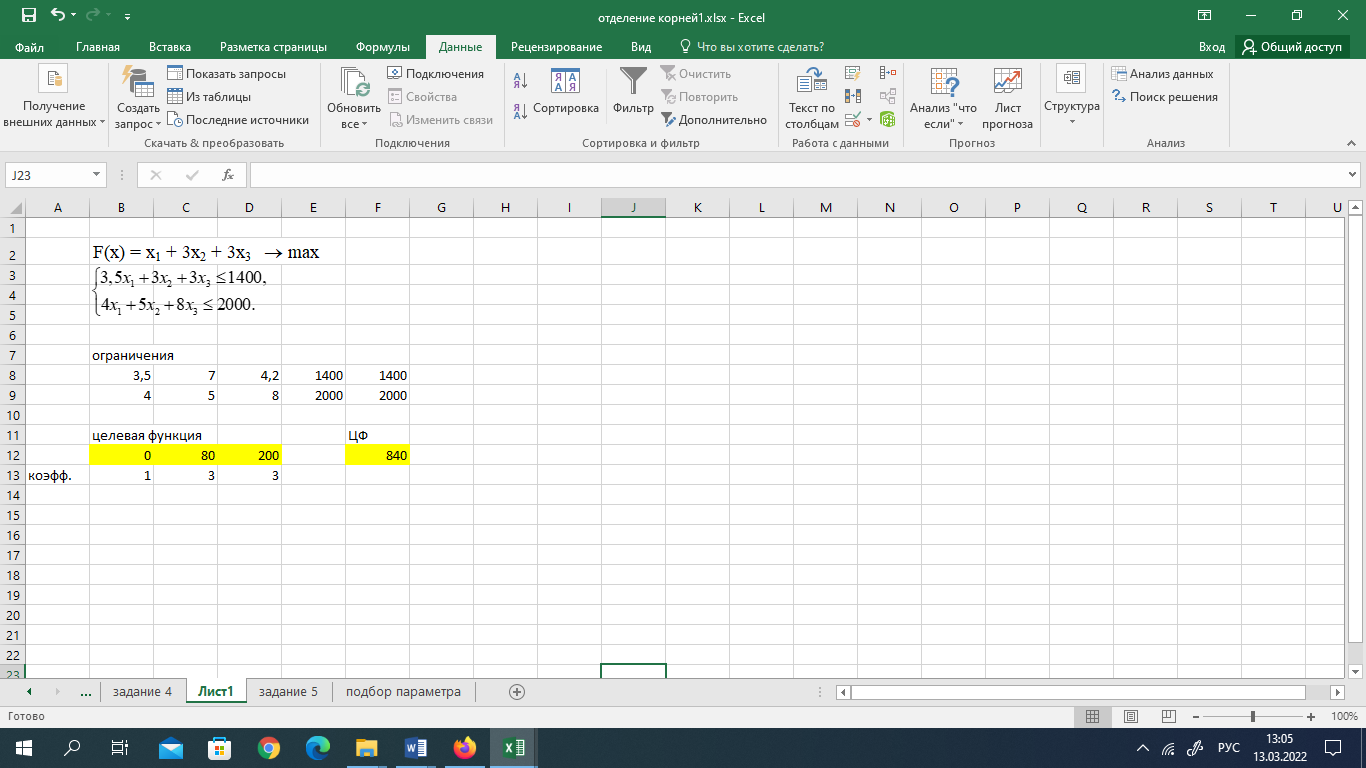 Транспортная задача
Решение: Опорный план перевозок найдем методом северо-западного угла и методом минимального элемента, проведем сравнение транспортных издержек по этим двум планам. Общее наличие груза у поставщиков 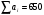 Общая потребность в грузе у потребителей 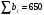 Так как 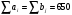 , то модель транспортной задачи является закрытой. , то модель транспортной задачи является закрытой.Решим задачу методом северо-западного угла: Опорный план должен содержать 3+5-1=7 заполненных клеток. Заполнение таблицы начинаем с левого верхнего угла, используем запасы поставщиков, спускаясь вниз полностью удовлетворяя потребности потребителей.
Получили опорный план: 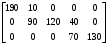 Общая стоимость перевозок: 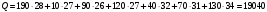 Решим задачу методом минимального элемента. Метод минимального элемента основан на выборе клетки с минимальным тарифом (на каждом шаге выбирают клетку с минимальным тарифом и рассматривают пункты назначения и пункты отправлений, соответствующие выбранной клетке).
1) C21 =18 – min; рассматриваем А2 и B1; исключаем клетки В1 из потребности А2 равны 60. 2) С13=18 –min; рассматриваем А1 и B3 исключаем клетки В3 из потребности А1 становится равным 80 3) С25=21 – min; рассматриваем А2 и B5 исключаем клетки А2 из потребности B5 становится равным 70 4) С15=24- min; рассматриваем А1 и B5 исключаем клетки B5 из запасов А1 становится равным 10 5) С12=27 - min; рассматриваем А1 и B2 исключаем клетки А1 из запасов В2 становится равным 90 6) С32=33; рассматриваем А3 и B2 исключаем клетки B2 из запасов А3 исключаем из потребностей. Опорный план: 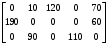 Общая стоимость перевозок: 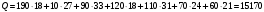 . . Сравнивая полученные результаты делаем вывод, что при нахождении плана методом минимальных элементов, общая стоимость перевозок значительно ниже, чем при нахождении методом северо-западного угла. Это основано на том, что метод северо-западного угла не ориентируется на тарифы. Уточним опорный план методом потенциалов. Считаем потенциалы клеток. За минимальное 0 выбираем ту строку, у которой больше заполненных клеток: V1=0. Считаем потенциалы строк и столбцов, используя заполненные клетки:
Считаем потенциалы незаполненных клеток
Так как есть клетка в которой вычисленный потенциал больше, чем необходимо, то составим цикл пересчета. Найдем потенциалы заполненных клеток.
Считаем потенциалы незаполненных клеток
Так как для каждой клетки выполняется равенство 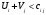 , то опорный план найден. , то опорный план найден.Опорный план: 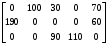 Общая стоимость перевозок: 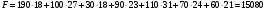 Проверим правильность нахождения решения с помощью надстройки Поиск решения. Запишем решение: 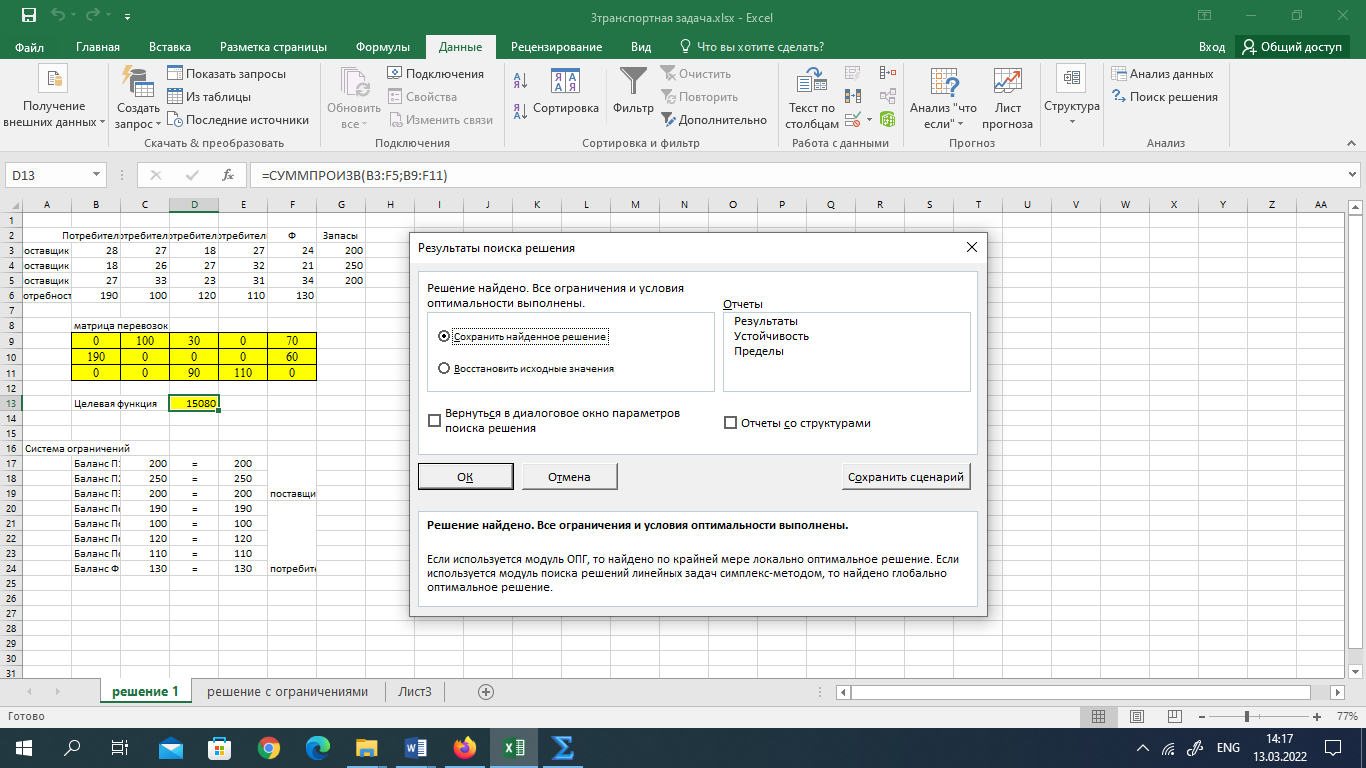 4. Решить с применением теорем двойственности F(x) =6 x1 -2x2 -4x3-3x4 min 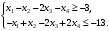 x1 0, x2 0, x3, х4 0. Решение: Упорядочим задачу линейного программирования. Решаем задачу на минимум. Так как если есть ограничения в виде "≤", то умножим данную строку на −1: F(x) =6 x1 -2x2 -4x3-3x4 min 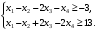 x1 0, x2 0, x3, х4 0. Вектор коэффициентов целевой функции прямой задачи: 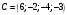 Свободные члены системы ограничений прямой задачи: B=(−3;13) Матрица коэффициентов прямой задачи: 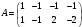 Так как целевая функция исходной задачи исследуется на минимум, до целевая функция двойственной задачи исследуется на максимум. Коэффициенты целевой функции двойственной задачи совпадают с свободными членами системы ограничений прямой задачи: Cдв=BT=(−3;13) Свободные члены двойственной задачи равны коэффициентам целевой функции прямой задачи 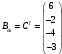 Матрица коэффициентов двойственной задачи равно матрице коэффициентов прямой задачи, взятой в транспонированном виде. 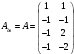 Количество переменных двойственной задачи равно количеству ограничений прямой задачи, а количество ограничений двойственной задачи равно количеству переменных прямой задачи. Двойственная задача линейного программирования: Q(y) =-3y1 +13y2 max 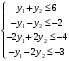 y1 0, y2 0. Решим задачу графическим методом: Построим допустимый многоугольник решений системы неравенств. Получили четырехугольник ABCD (рис. 4.1). 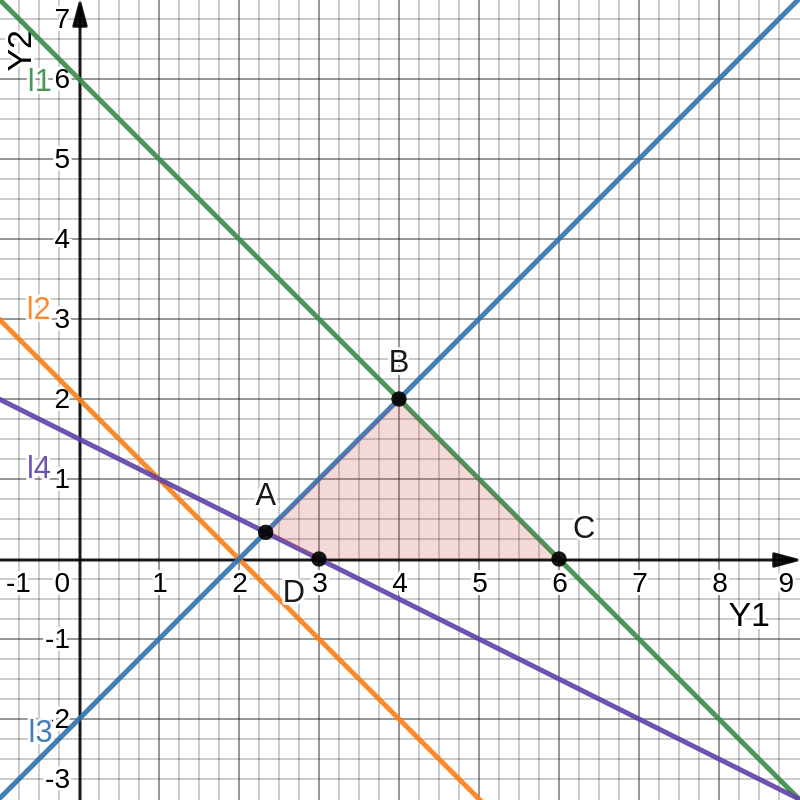 Рис. 4.1 Построим линию уровня целевой функции Q(y) = -3y1 + 13y2, и градиент целевой функции 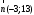 . . Передвигая линию уровня вдоль градиента параллельно самой себе, находим точки экстремума. Точкой минимума (точкой входа) будет точка С. Точкой максимума – точка В (рис. 4.2). Найдем координаты точки В. 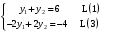 Решая систему линейных уравнений, находим координаты точки 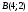 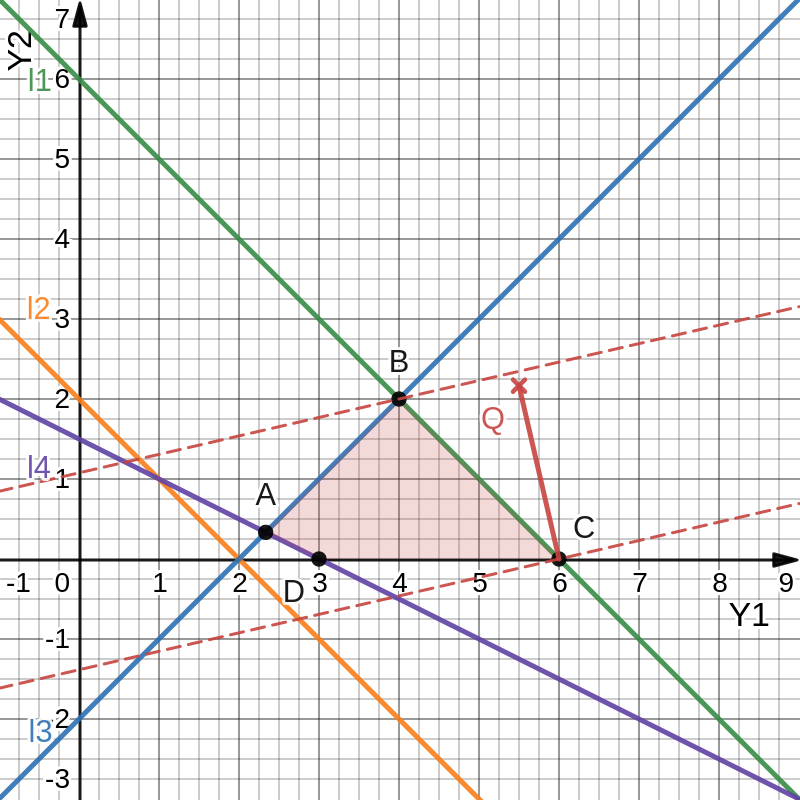 Рис. 4.2. Двойственный оптимальный план: 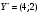 . В результате получим Q*(y) =14, . В результате получим Q*(y) =14, 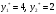 . . Для решения двойственной задачи используем теоремы двойственности. По теореме 1 исходная (прямая) задача также имеет оптимальный план 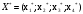 Чтобы найти X*, подставим 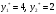 в систему уравнений из теоремы 2. в систему уравнений из теоремы 2.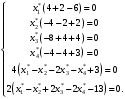 Получаем 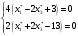 Решая систему, находим 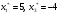 Оптимальный план: 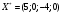 Решить графическим методом F(x1,х2) = 2x1 + 4x2 - x12- 2x22 max 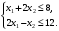 x1 0, x2 0. Решение: Сначала построим область допустимых решений в первой четверти, ограниченную прямыми: 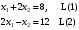 Получаем выпуклый многоугольник ОABC (рис. 5.1) 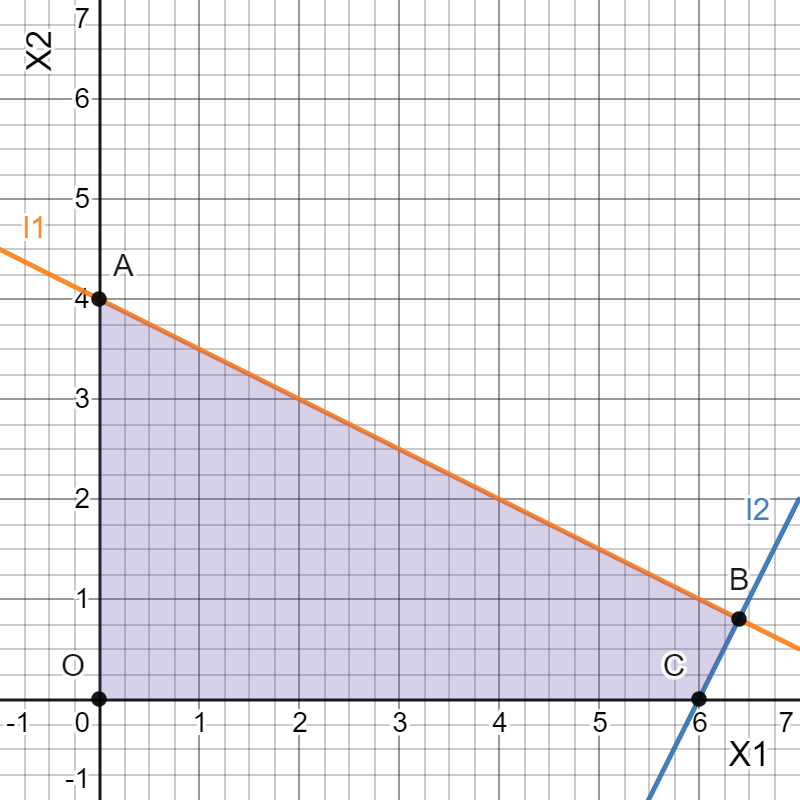 Рис. 5.1 Построение области допустимых значений Преобразуем целевую функцию 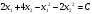 Получим 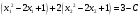 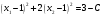 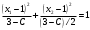 - уравнение эллипса с центром в точке (1;1) - уравнение эллипса с центром в точке (1;1)Теперь строим линии уровня целевой функции: концентрические эллипсы с центром в точке (1,1). Чем больше радиус, тем меньше значение целевой функции. Таким образом, наибольшее значение функция примет в точке (1;1), так как центр эллипса находится в области допустимых значений функции. 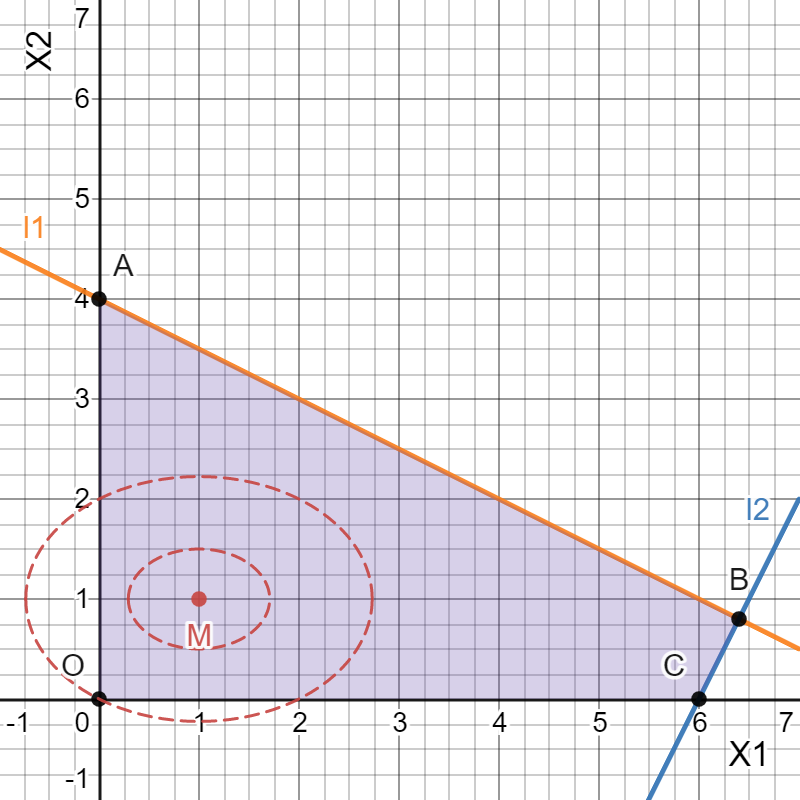 Максимальное значение функции: F(x1,х2) = 2x1 + 4x2 - x12- 2x22=2+4-1-2=3 6. Решить методом множителей Лагранжа Используя метод множителей Лагранжа найти условный экстремум функции 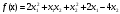 при при 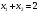 , , 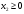 Решение: Решая задачу графически, можно заметить, что максимального значения функция не достигает. Минимальное значение найдем, используя метод множителей Лагранжа. 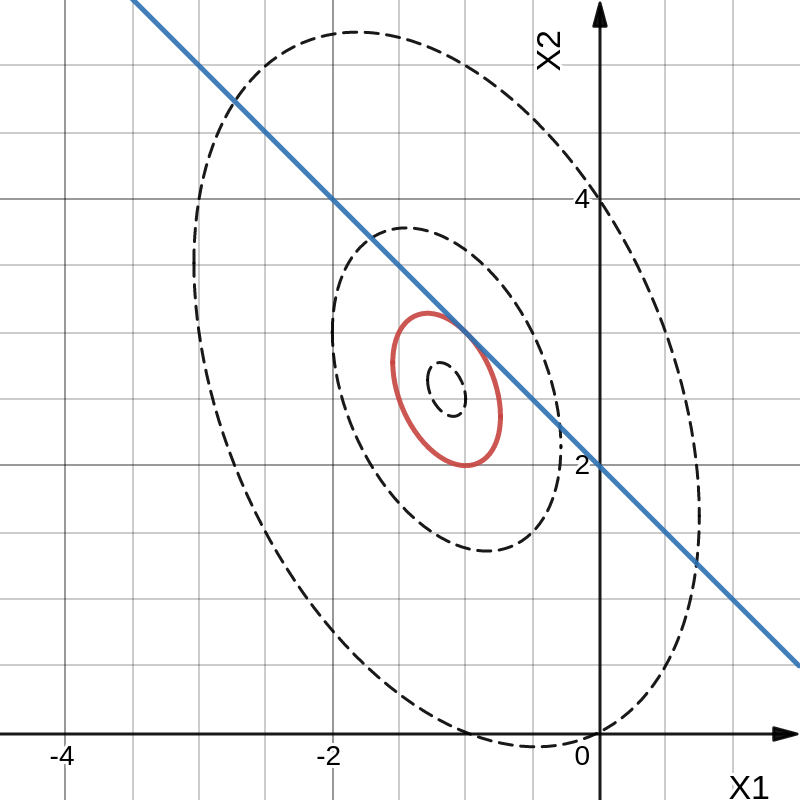 Обозначив 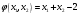 , составим функцию Лагранжа: , составим функцию Лагранжа: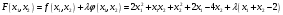 Найдем частные производные: 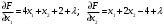 Запишем систему уравнений для определения стационарных точек функции Лагранжа: 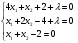 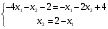 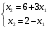 Решая систему находим координаты стационарной точки 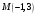 Выясним характер экстремума в каждой стационарной точке: 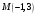 Вычислим определитель Н в точке: 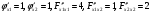 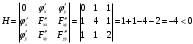 Следовательно, в точке 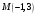 функция функция 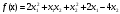 имеет условный минимум, имеет условный минимум, 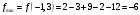 . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 10 27
10 27
 120 18
120 18 70 24
70 24 190 18
190 18
 26
26 60 21
60 21 90 33
90 33