Эконометрика. Задание Парная регрессия и корреляция

• Название: Задание Парная регрессия и корреляция
• Дата: 02.11.2021
• Размер: 119.8 Kb.
• Имя файла: Эконометрика.docx
• Тип: Документы; #261418
• страница: 3 из 3

Задание № 3. Временные ряды

1. 
   Построить график временного ряда.
   
2. 
   Построить аддитивную и мультипликативную модели временного ряда.
   
3. 
   Оценить качество каждой модели и выбрать лучшую из них.
   
4. 
   Оформить выводы в аналитической записке.
   

Исходные данные:

Год	Центральный федеральный округ (средняя пенсия)
2000	823,5
2001	1148
2002	1480,5
2003	1766,5
2004	2031,9
2005	2536,7
2006	2837,1
2007	3657,5
2008	4518,8
2009	6146,7

Решение:

Рассчитаем параметры аддитивной модели временного ряда.

Y=T+S+E

Таблица 3.1

Расчет оценок циклической компоненты:

	Года	Средняя пенсия	Итого за 2 года	Скользящая средняя за 2 года	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2000	823,5
2	2001	1148	1971,5	985,75
3	2002	1480,5	2628,5	1314,25	1150,00	330,50
4	2003	1766,5	3247	1623,50	1468,88	297,63
5	2004	2031,9	3798,4	1899,20	1761,35	270,55
6	2005	2536,7	4568,6	2284,30	2091,75	444,95
7	2006	2837,1	5373,8	2686,90	2485,60	351,50
8	2007	3657,5	6494,6	3247,30	2967,10	690,40
9	2008	4518,8	8176,3	4088,15	3667,73	851,08
10	2009	6146,7	10665,5

Найдем оценки циклической компоненты как разность между фактическими

уровнями ряда и центрированными скользящими средними. Используем эти

оценки для расчета значений циклической компоненты S (табл. 3.4). Для этого найдем средние оценки циклической компоненты Si. В моделях с циклической компонентой обычно предполагается, что циклические воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений циклической компоненты за восемь лет должна быть равна нулю.

Для данной модели имеем:

257,66+477,66=735,32

Определим корректирующий элемент:

K=735,32/2 =367,6

Таблица 3.2

Расчет значений циклической компоненты.

Показатели	1	2
1	-	-
2	-	-
3	330,5	297,63
4	270,55	444,95
5	351,5	690,4
6	851,08	-
Всего за период	1803,63	1432,98
Средняя оценка циклической компоненты, Si	257,66	477,66
Скорректированная циклическая компонеты, Si	-110,00	110,00

Рассчитаем скорректированные значения циклической компоненты как раз-

ности между их средними оценками и корректирующим коэффициентом k:

Si=Si-k

Таблица 3.3

Расчет компонентов аддитивной модели

t	у	s	T+E	Tt	Tt+Si	E	E^2
1	823,5	-110	933,5	2700,54	2590,54	-1767,04	3122430,36
2	1148	110	1038	2701,44	2811,44	-1663,44	2767032,63
3	1480,5	-110	1590,5	2702,34	2592,34	-1111,84	1236188,19
4	1766,5	110	1656,5	2703,24	2813,24	-1046,74	1095664,63
5	2031,9	-110	2141,9	2704,14	2594,14	-562,24	316113,82
6	2536,7	110	2426,7	2705,04	2815,04	-278,34	77473,16
7	2837,1	-110	2947,1	2705,94	2595,94	241,16	58158,15
8	3657,5	110	3547,5	2706,84	2816,84	840,66	706709,24
9	4518,8	-110	4628,8	2707,74	2597,74	1921,06	3690471,52
10	6146,7	110	6036,7	2708,64	2818,64	3328,06	11075983,36
55	26947,2						24146225,05

Уравнение тренда имеет вид:

Tt=a+bt

b=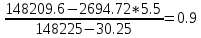

a=2694,72+0,9*5.5=2699.67

T=2699,67+0,9t

Для оценки качества аддитивной модели используем сумму квадратов

полученных абсолютных ошибок:

Е=у-(Т+S) = 1-24146225,05/(26947,2-2694,72)²=0,95

Аддитивная модель объясняет 95 % общей вариации уровней временного ряда.

Рассчитаем параметры мультипликативной модели временного ряда:

Y=T*S+E

Найдем оценки циклической компоненты как частное от деления

фактических уровней ряда на центрированные скользящие средние.

Таблица 3.4

Расчет оценок циклической компоненты

	Года	Средняя пенсия	Итого за 2 года	Скользящая средняя за 2 года	Центрированная скользящая средняя	Оценка циклической компоненты
1	2000	823,5
2	2001	1148	1971,5	985,75
3	2002	1480,5	2628,5	1314,25	1150,00	1,29
4	2003	1766,5	3247	1623,50	1468,88	1,20
5	2004	2031,9	3798,4	1899,20	1761,35	1,15
6	2005	2536,7	4568,6	2284,30	2091,75	1,21
7	2006	2837,1	5373,8	2686,90	2485,60	1,14
8	2007	3657,5	6494,6	3247,30	2967,10	1,23
9	2008	4518,8	8176,3	4088,15	3667,73	1,23
10	2009	6146,7	10665,5

Эти оценки используются для расчета циклической компоненты S. Для этого найдем средние за каждые период оценки циклической компоненты Si.

Циклические воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений циклической компоненты за 2 года должна быть равна 2.

Таблица 3.5

Расчет значений циклической компоненты

Показатели	1	2
1	-	-
2	1,29	1,2
3	1,15	1,21
4	1,14	1,23
5	1,23
Всего за период	4,81	3,64
Средняя оценка циклической компоненты, Si	1,20	1,21
Скорректированная циклическая компонеты, Si	1,00	1,00

Для данной модели имеем:

1,20+1,21=2,42

Определим корректирующий элемент:

K=2/2,42=0,82

Рассчитаем скорректированные значения циклической компоненты как произведение между их средними оценками и корректирующим коэффициентом k: Si=Si*k

Таблица 3.6

Расчет компонентов мультипликативной модели

t	у	s	T+E	Tt	Tt+Si	E	E^2
1	823,5	1	823,5	2700,54	2701,54	-1878,04	3527034,24
2	1148	1	1148	2701,44	2702,44	-1554,44	2416283,71
3	1480,5	1	1480,5	2702,34	2703,34	-1222,84	1495337,67
4	1766,5	1	1766,5	2703,24	2704,24	-937,74	879356,31
5	2031,9	1	2031,9	2704,14	2705,14	-673,24	453252,10
6	2536,7	1	2536,7	2705,04	2706,04	-169,34	28676,04
7	2837,1	1	2837,1	2705,94	2706,94	130,16	16941,63
8	3657,5	1	3657,5	2706,84	2707,84	949,66	901854,12
9	4518,8	1	4518,8	2707,74	2708,74	1810,06	3276317,20
10	6146,7	1	6146,7	2708,64	2709,64	3437,06	11813381,44
55	26947,2						24808434,45

Уравнение тренда имеет вид:

Tt=a+bt

b=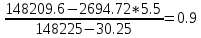

a=2694,72+0,9*5.5=2699.67

T=2699,67+0,9t

Для оценки качества мультипликативной модели используем сумму квадратов полученных абсолютных ошибок:

R=1- 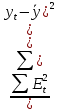= 1-24808434/(26947,2-2694,72)²=0,97

Мультипликативная модель объясняет 97 % общей вариации уровней временного ряда.

Список литературы

1. 
   Орлов А.И. Эконометрика, Учебник. М.: Экзамен, 2009
   
2. 
   Практикум по эконометрике: Учебное пособие/Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2012.
   
3. 
   Тихомиров Н.П., Дорохина Е.Ю. Эконометрика. М.: Экзамен, 2010.
   
4. 
   Эконометрика. Под ред. И.И. Елисеевой. М.: Финансы и статистика, 2007.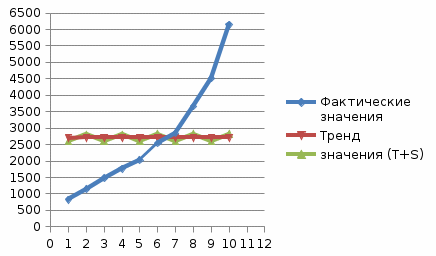
   

Рис. 4 Средняя пенсия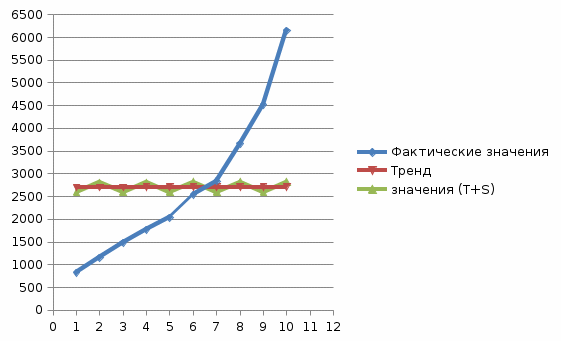


Рис. 5 Средняя пенсия