Эконометрика. Задание Парная регрессия и корреляция
 Скачать 119.8 Kb. Скачать 119.8 Kb.
|
|
Задание №2 . Множественная регрессия и корреляция Построить уравнение множественной регрессии в стандартизованной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с 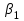 и и  , пояснить различия между ними. , пояснить различия между ними.Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними. Рассчитать общий и частные F-критерии Фишера. Оценить полученные результаты. Оформить выводы в аналитической записке. Решение: Таблица 2.1 Исходные данные
Система трех линейных уравнений с тремя неизвестными b0, b1, b2: ∑yi = nb0 + b1∑x1i + b2∑x2i ∑x1iyi = b0∑x1i + b1∑x1i2 + b2∑x1ix2i ∑x2iyi = b0∑x2i + b1∑x1ix2i + b2∑x2i2 Таблица 2.2.
Для наших данных система уравнений имеет вид: 107040.9 = 18 b0 + 87334b1 + 10682b2 522262495.2 = 87334b0 + 434065038b1 + 58933269b2 65659346.1 = 10682b0 + 58933269b1 + 12570628b2 Решая систему методом Крамера, находим: b0 = 4851.75 b1 = 0.21 b2 = 0.0994 Уравнение регрессии: Y = 4851.75 + 0.21 X1 + 0.0994 X2 Таблица 2.3.
Коэффициенты регрессии bi можно также найти по следующим формулам: где ryx1, ryx2, rx1x2 - коэффициенты парной корреляции между результатом и каждым из факторов и между факторами; s(x1), s(x2) - среднее квадратическое отклонение 1-го и 2-го факторов соответственно; s(y) - среднее квадратическое отклонение результативного признака. Параметр a можно определить по формуле: Указанные параметры рассчитаны в разделе Оценка мультиколлинеарности факторов. 2. Анализ качества эмпирического уравнения множественной линейной регрессии. Построение эмпирического уравнения регрессии является начальным этапом эконометрического анализа. Первое же построенное по выборке уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей оценкой является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки, которая проводится по следующим направлениям: • проверка статистической значимости коэффициентов уравнения регрессии; • проверка общего качества уравнения регрессии; • проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК). Прежде, чем проводить анализ качества уравнения регрессии, необходимо определить дисперсии и стандартные ошибки коэффициентов, а также интервальные оценки коэффициентов. При этом: где m=2 – количество объясняющих переменных модели. Стандартные ошибки коэффициентов: Таблица 2.4
Парные коэффициенты корреляции. Для y и x1 Средние значения Дисперсия Среднеквадратическое отклонение Коэффициент корреляции Для y и x2 Средние значения Дисперсия Среднеквадратическое отклонение Коэффициент корреляции Для x1 и x2 Средние значения Дисперсия Среднеквадратическое отклонение Коэффициент корреляции Матрица парных коэффициентов корреляции.
При оценке мультиколлинеарности факторов следует учитывать, что чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. Для отбора наиболее значимых факторов xi учитываются следующие условия: - связь между результативным признаком и факторным должна быть выше межфакторной связи; - связь между факторами должна быть не более 0.7; - при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними; Более объективную характеристику тесноты связи дают частные коэффициенты корреляции, измеряющие влияние на результат фактора xi при неизменном уровне других факторов. Частные коэффициенты корреляции. Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и xi) при условии, что влияние на них остальных факторов (xj) устранено. Теснота связи не сильная Теснота связи низкая. Теснота связи не сильная Теснота связи умеренная Теснота связи низкая. Теснота связи умеренная Уравнение регрессии в стандартизированном масштабе. Другим видом уравнения множественной регрессии может быть уравнение регрессии в стандартизированном масштабе: ty = β1tx1 + β2tx2. где βi – стандартные коэффициенты регрессии. К уравнению множественной регрессии в стандартизированном масштабе применим МНК. Стандартизированные коэффициенты регрессии (β-коэффициенты) определяются из следующей системы уравнений: ryx1 = β1 + β2rx2x1 ryx2 = β1rx2x1 + β2 Связь коэффициентов множественной регрессии bi со стандартизированными коэффициентами βi описывается соотношением: Параметр α определяется как: α = 5946.72 - 0.21 • 4851.89 - 0.0994 • 593.44 = 4851.75 4. Оценка тесноты связи. 4. Теснота связи результативного признака с факторными определятся величиной коэффициента линейной множественной корреляции и детерминации, который могут быть исчислены на основе матрицы парных коэффициентов корреляции: Более объективную оценку качества построенной модели дает скорректированный индекс множественной детерминации, учитывающий поправку на число степеней свободы: где n- число наблюдений, m – число факторов. Сравнительная оценка влияния анализируемых факторов на результативный признак. 5. Сравнительная оценка влияния анализируемых факторов на результативный признак производится: - средним коэффициентом эластичности, показывающим на сколько процентов среднем по совокупности изменится результат y от своей средней величины при измени фактора xi на 1% от своего среднего значения; Частный коэффициент эластичности E1 < 1. Следовательно, его влияние на результативный признак Y незначительно. Частный коэффициент эластичности E2 < 1. Следовательно, его влияние на результативный признак Y незначительно. - β–коэффициенты, показывающие, что, если величина фактора изменится на одно среднеквадратическое отклонение Sxi, то значение результативного признака изменится в среднем на β своего среднеквадратического отклонения; - долю каждого фактора в общей вариации результативного признака определяют коэффициенты раздельной детерминации (отдельного определения): d2i = ryxiβi. d21 = 0.82 • 0.000143 = 0.000118. d22 = 0.78 • 8.6E-5 = 6.7E-5. При этом должно выполняться равенство: d21 + d22 = R2yx1x2. Результаты сравнительного анализа факторов оформляются в таблице: Проверка гипотезы о статистической значимости уравнения регрессии. Проверка гипотезы H0 о статистической значимости уравнения регрессии и показателя тесноты связи (R2 = 0) производится по F-критерию Фишера сравнением Fфакт с Fтабл. Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели. Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой. где m – число факторов в модели. Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму: 1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α. 2. Далее определяют фактическое значение F-критерия: где m=2 для множественной регрессии с двумя факторами. 3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 2 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2-1. 4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом. Табличное значение критерия со степенями свободы k1=2 и k2=15, Fkp = 3.68 Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). Частные критерии. Частные критерии Fx1 и Fx2 оценивают статистическую значимость включения факторов x1 и x2 в уравнение множественной регрессии и целесообразность включения в уравнение одного фактора после другого, т.е. Fx1 оценивает целесообразность включения в уравнение x1 после включения в него фактора x2. Соответственно Fx2 указывает на целесообразность включения в модель фактора x2 после включения фактора x1. Поскольку фактическое значение F > Fkp, то коэффициент Fx1 статистически значим, т.е. целесообразно включать в уравнение x1 после включения в него фактора x2. Поскольку фактическое значение F < Fkp, то коэффициент Fx2 статистически не значим, т.е. не целесообразно включать в уравнение x2 после включения в него фактора x1. |
