сопромуть. Задание Расчет стержня на прочность и

• Название: Задание Расчет стержня на прочность и
• Анкор: сопромуть
• Дата: 16.06.2022
• Размер: 1.13 Mb.
• Имя файла: Sopromat_okonchatelno.doc
• Тип: Конспект; #595911
• страница: 3 из 5

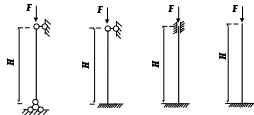
Таблица 10

Виды закрепления стержней

Номер расчетной схемы	I	II	III	IV
Конструкция опорных закреплений сжатой стойки

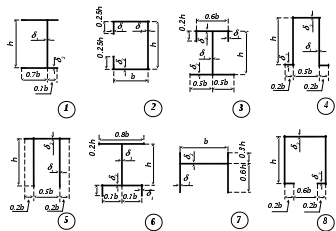
Задание № 9. Определение секториальных

характеристик тонкостенного стержня
Для заданного типа поперечного сечения тонкостенного стержня требуется:

1. 
   определить положения центра тяжести сечения;
   
2. 
   построить эпюры линейных координат z и y;
   
3. 
   по построенным эпюрам вычислить величину осевых моментов инерции сечения I_zсиI_yс ;
   
4. 
   построить эпюру секториальных координат ;
   
5. 
   перемножением эпюр zиyна эпюру рассчитать секториально-линейные статические моменты сечения S_zи S_y и определить координаты центра изгиба;
   
6. 
   построить эпюру главных секториальных координат _о;
   
7. 
   используя эпюру _о, вычислить главный секториальный момент инерции сечения I_o;
   
8. 
   вычислить момент инерции сечения при чистом кручении I_t .
   

Типы поперечного сечения балки приведены на рис. 8. Исходные данные о размерах сечения следует принять по табл. 11.

Перед решением этой задачи необходимо изучить материал, изложенный в [1], [2], [11].



Рис. 8
Таблица 11

Исходные данные к заданию № 9

№ строки	h, см	b, см	1 , см	2 см
1	20	24	1,2	1,4
2	22	28	1,1	1,3
3	24	22	1,2	1,3
4	26	20	1,0	1,1
5	28	26	1,4	1,2
6	30	18	1,3	1,2
7	32	26	1,4	1,2
8	34	24	1,0	1,1
9	36	22	1,2	1,3
10	20	30	1,3	1,5
11	24	28	1,2	1,4
12	26	32	1,4	1,2
13	28	20	1,1	1,3
14	30	26	1,4	1,5
15	32	24	1,3	1,4

Задание № 10. Расчет пластины методом Ритца
Для прямоугольной пластины, загруженной равномерно распределенной нагрузкой интенсивностью q и сосредоточенной силой величиной F, расположенной в точке K с координатами x_F, y_F при заданном выражении функции прогибов требуется:

1. 
   установить условия опирания пластины;
   
2. 
   методом Ритца определить коэффициент C;
   
3. 
   построить эпюры прогибов для указанных сечений пластин;
   
4. 
   построить эпюры изгибающих моментов, поперечных сил, крутящих моментов;
   
5. 
   построить эпюры нормальных и касательных напряжений для указанных сечений.
   

Расчетная схема плиты приведена на рис. 9.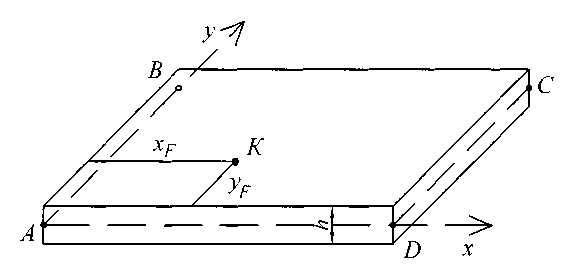



Рис. 9
Из табл. 12 требуется выбрать функцию прогибов, удовлетворяющую граничным условиям на гранях пластины, т.е.
w(x,y) = C f _i (x)_j (y),
где i – номер функции в направлении оси х; j – номер функции в направлении оси y.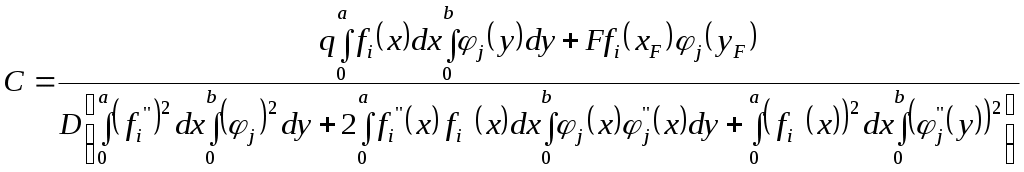
.
Цилиндрическая жесткость .

Эпюры внутренних усилий построить по формулам:
;
;
;
;
.
Эпюры строить, исходя из того, что в заданном сечении пластины ее длину и ширину разделить на четыре части.

Эпюры напряжений в заданной точке пластины по ее толщине построить согласно формулам:
;
;
,
где z – расстояние по толщине пластины от ее нейтральной плоскости до точки, в которой определяется напряжение.

Исходные данные для расчета следует принять по табл. 13.

Таблица 12

Функции прогибов

Вариант	Функция направления х	Функция направления у
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Таблица 13

Исходные данные к заданию № 10

Вариант	а, см	b, см	h, см	Е, МПа		q, кН/м2	F, кН	xF, см	уF, см
1	280	140	8	1,0105	0,30	30	30	60	35
2	320	160	10	1,2105	0,31	32	32	80	30
3	360	180	12	1,4105	0,30	34	30	60	30
4	400	200	14	1,6105	0,30	40	30	60	40
5	440	220	16	1,8105	0,30	38	30	110	55
6	480	240	18	2,0105	0,31	40	32	120	60
7	520	260	20	2,1105	0,30	42	30	120	70
8	560	280	22	2,2105	0,31	44	32	130	70
9	600	300	24	2,1105	0,31	40	32	140	80
10	640	320	26	1,8105	0,30	38	34	130	40
11	460	230	12	1,2105	0,31	36	32	100	60
12	520	260	16	1,4105	0,30	46	34	120	75
13	560	280	20	1,6105	0,31	32	36	130	50
14	580	240	24	1,8105	0,31	34	30	150	45
15	620	310	26	2,0105	0,30	40	32	90	80