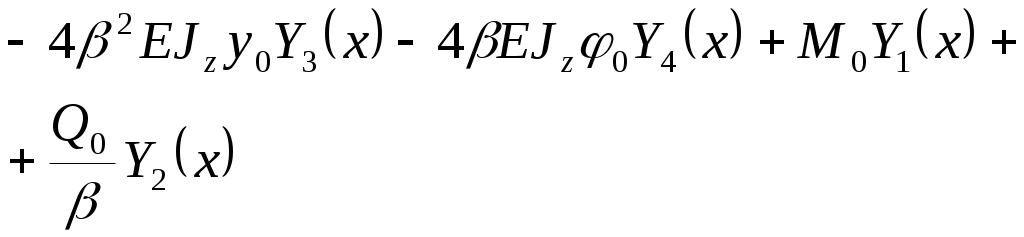сопромуть. Задание Расчет стержня на прочность и
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
|
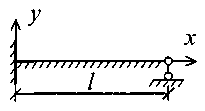
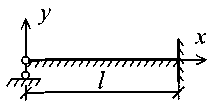
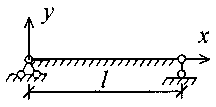
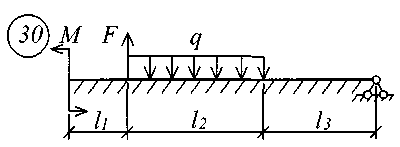
Задание № 11. Расчет балки на сплошном упругом основании Для балки, лежащей на сплошном упругом основании требуется определить внутренние усилия и перемещения, используя соответствующие уравнения метода начальных параметров. Работа выполняется в два этапа. На первом этапе необходимо записать уравнения деформаций и внутренних усилий для каждого участка балки. Напряженно-деформированное состояние балки, лежащей на сплошном упругом основании, зависит от жесткостных характеристик балки и упругого основания. Этими характеристиками являются: EJz – изгибная жесткость балки; где Е – модуль упругости материала балки, кН/м2; Jz – момент инерции поперечного сечения балки, м4; K0 – коэффициент податливости упругого основания, зависящий от свойств грунта, кН/м3; b – ширина поперечного сечения балки, м. При расчете методом начальных параметров начало координат выбирается в крайней левой точке балки. Поскольку реакция упругого основания изменяется непрерывно по длине балки, то для построения криволинейных эпюр деформаций и внутренних усилий необходимо определить их значения для нескольких точек по длине. Начальные параметры зависят от граничных условий. В табл. 14 представлены уравнения в зависимости от действующих внешних нагрузок. В этих уравнениях y0, 0, M0, Q0 – начальные параметры, из которых два всегда равны нулю (табл. 15). Неизвестные начальные параметры определяются из условий закрепления правого края балки. В уравнения y, , M, Q (табл. 14) входят функции Y1(x), Y2(x),Y3(x),Y4(x), названные функциями Крылова-Коши, значения которых определяются в зависимости от аргумента x, где x – координаты точек балки в принятой системе координат: Y1(x) = chx cosx; Y2(x) = 0,5(chx sinx + shx cosx); Y3(x) = 0,5shx sinx; Y4(x) = 0,25(chx sinx – shx cosx). В зависимости от характера действующих нагрузок и от условий закреплений левого конца балки для каждого участка необходимо записать уравнение по форме, представленной в табл. 14. Поскольку при составлении уравнений для различных сечений каждый раз рассматривается часть балки слева от сечения, то в уравнение для каждого последующего сечения входят все слагаемые уравнения в предыдущих сечениях. Поэтому запись уравнений для любого сечения может быть представлена в виде табл. 16. Исходные данные для расчета на ЭВМ 1) Фамилия студента и номер группы. 2) Коэффициент жесткости, жесткость балки, внешние нагрузки и граничные условия. Коэффициент жесткости должен иметь размерность 1/м. Таблица 14 Начальные параметры
Таблица 15 Зависимость от закрепления балки
Жесткость балки EJz имеет размерность кНм2. При записи исходных данных эта величина должна быть умножена на 10-5. Внешние нагрузки записываются в следующем порядке: M, F,q. Для определения неизвестных начальных параметров необходимо описание граничных условий. Вводится условная нумерация параметров: y = 1; = 2; М = 3; Q = 4. В качестве исходных данных в программу вводятся последовательно номера начальных параметров, не равных нулю, и номера известных параметров на правом конце балки. Например, для балки
граничные условия записываются так: 1 2 1 3. 3) Коэффициенты уравнений для всех участков балки (табл. 16). Таблица 16 Коэффициенты уравнений
В табл. 16 приняты следующие обозначения: Aij – коэффициенты слагаемых, содержащих начальные параметры; Bij – коэффициенты слагаемых от действия изгибающих моментов; Сij – коэффициенты слагаемых от действия сосредоточенных сил; Dij – коэффициенты слагаемых от действия равномерно распределенной нагрузки. Если в начале координат приложен изгибающий момент или сосредоточенная сила, то коэффициент слагаемых от действия этих нагрузок записываются в таблице в графахA3j или A4j, так как эти нагрузки будут являться известными начальными параметрами. Если на конце балки приложен изгибающий момент или сосредоточенная сила, то коэффициенты от действия этих нагрузок записываются в таблице в графах В3j или С3j. При заполнении таблицы для уравнений y(x) и (x) все коэффициенты, кроме тех, которые при y0 и 0, должны быть умножены на 105; для уравнений M(x) и Q(x) коэффициенты при y0 и 0 должны быть умножены на 10-5. Если какое-либо слагаемое отсутствует, то в соответствующей графе ставится ноль. 4) Приложение внешних нагрузок и размеры балки (табл. 17). Таблица 17 Исходные данные по нагрузке и размерам
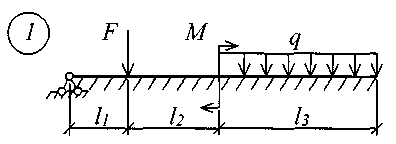
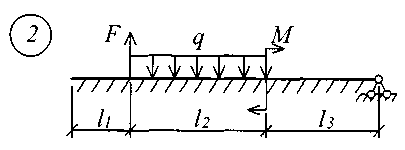
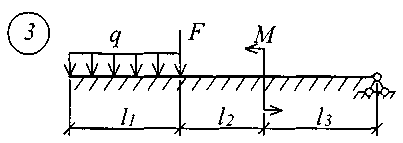
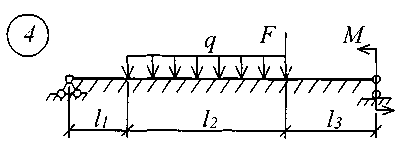
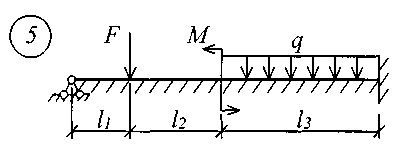
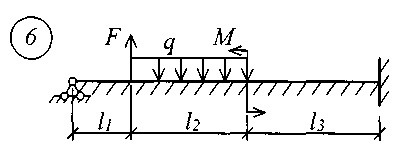
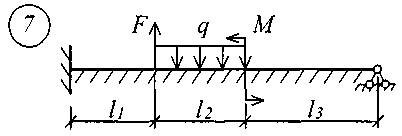
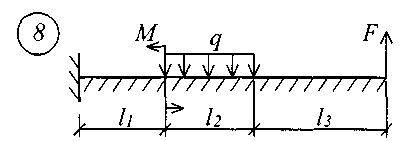
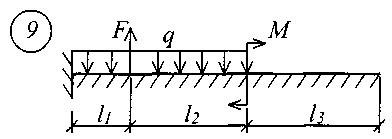
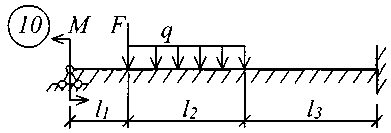
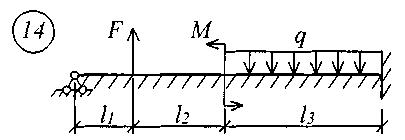
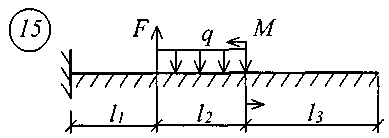
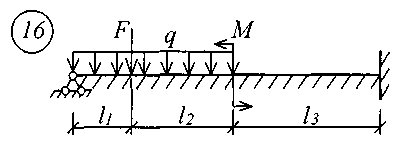
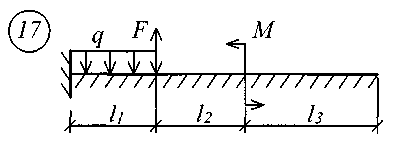
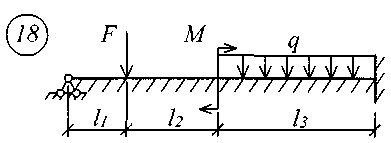
В табл. 17 приняты следующие обозначения: А, В – расстояние от начала координат до точки приложения соответственно момента или сосредоточенной силы; С2, С3 – расстояние от начала координат до начала действия равномерно распределенной нагрузки соответственно на втором и третьем участках балки; D2, D3 – расстояние от начала координат до конца действия равномерно распределенной нагрузки соответственно на втором и третьем участках балки; L – полная длина балки; L1, L2 – расстояние от начала координат до границы соответственно первого и второго участков. Все размеры принимаются в метрах. Пример записи исходных данных Для балки (рис. 10) требуется записать исходные данные для расчета на ЭВМ при следующих условиях: F = 400 кН; М = 200 кНм; q = 100 кН/м; Е = 8106 кН/м2; l1 = 3 м;l2 = 2 м;l3 = 2 м;l = 7 м;K0 = 6,2104 кН/м3. Балка прямоугольного сечения шириной b = 1,0 м и высотой h = 0,6 м. 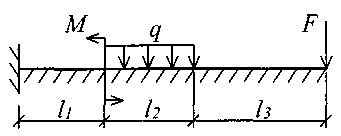 Рис. 10. Расчетная схема Определение расчетных параметров: Определение начальных параметров в соответствии с табл. 15. y0 = 0; 0 = 0; M0 0; Q0 0; yl 0; l 0; Ml= 0; Ql = F = 400 кН. Для определения неизвестных начальных параметров M0 и Q0 записываем уравнения: Ml= 0 и Ql = F. Определение начальных параметров выполняется на ЭВМ. Для каждого участка балки составляются уравнения y, , М и Q. Запись исходных данных для ЭВМ выглядит следующим образом: 1) Макеев С.А. 22МТ 2) 0,572 1,44 -200 400 100 3 4 3 4 3) 0 0 2,122493 3,711 0 -424,498 0 162,178 0 -1484,258 0 0 0 1,214 2,12249 0 -242,812 0 -371,064 0 -848,996 0 0 0 1 1,748 0 -200 0 -305,638 0 -699,301 0 0 0 -2,289 1 0 457,6 0 -174,825 0 -400 0 4) 3 7 3 0 0 5 7 3 5 Для решения задачи исходные данные приведены в табл. 18, расчетные схемы балок показаны на рис. 11.
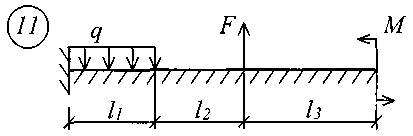
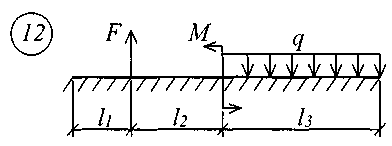
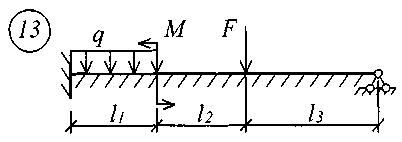
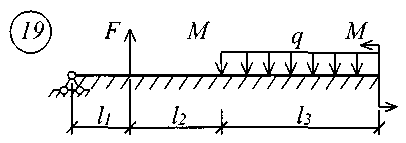
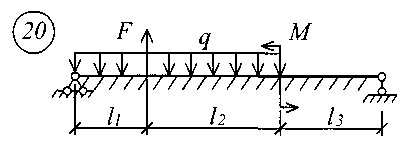
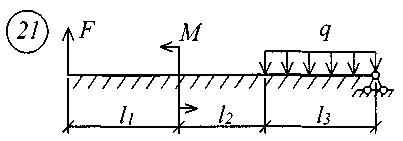
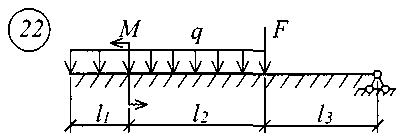
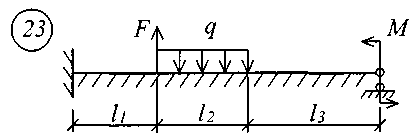
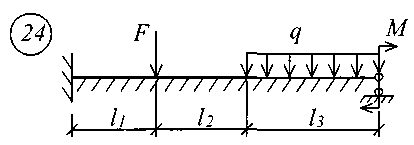
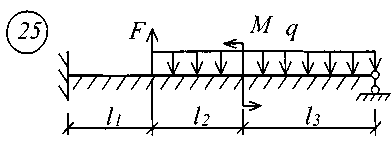
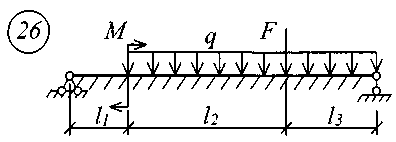
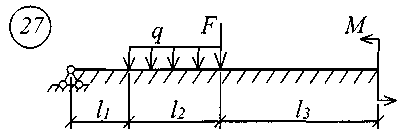
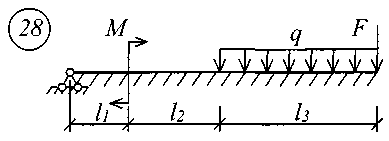
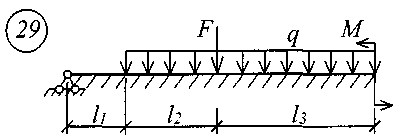
Рис. 11 (начало)
Рис. 11 (окончание) Таблица 18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

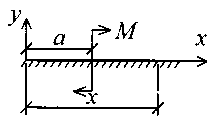
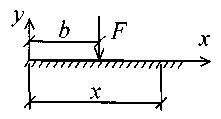
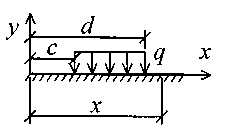
 (x)
(x)