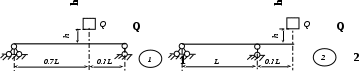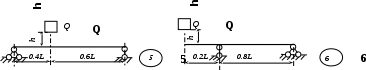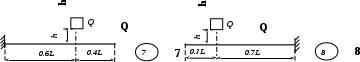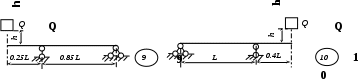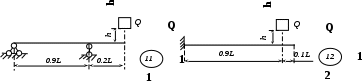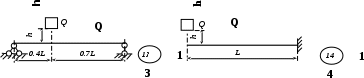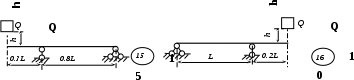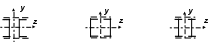сопромуть. Задание Расчет стержня на прочность и
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
|
Исходные данные к заданию № 3
Для выполнения этой задачи предварительно следует изучить теоретический материал, изложенный в [1], [2], сведения о геометрических характеристиках прокатных профилей (сортаменты) приводятся в этих учебниках и в справочниках [6], [8], [9].
Рис. 3 (начало)
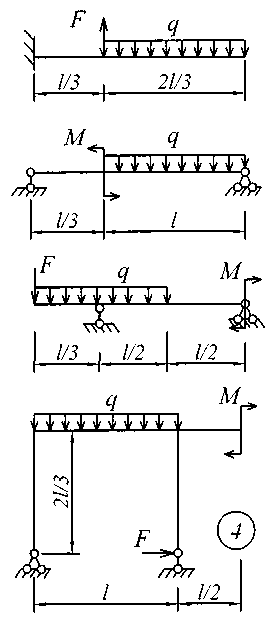
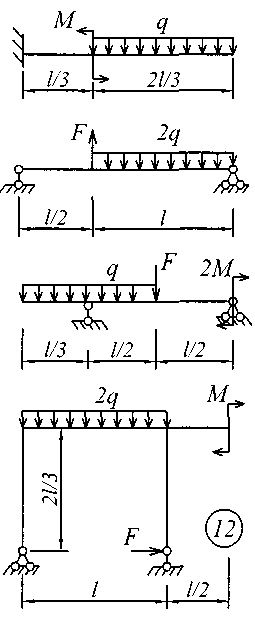
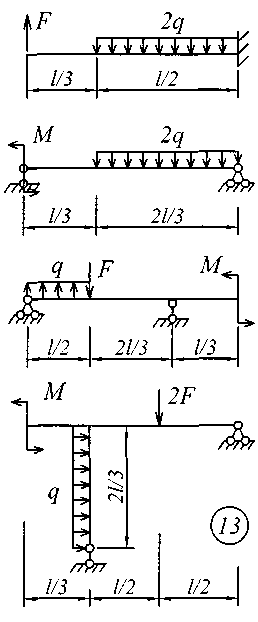
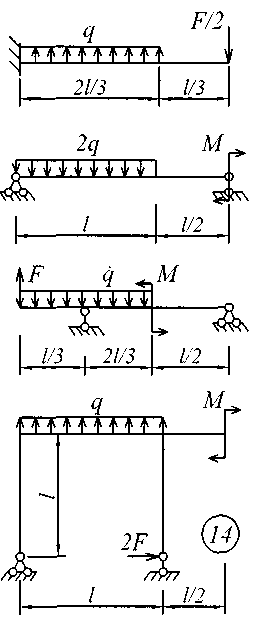
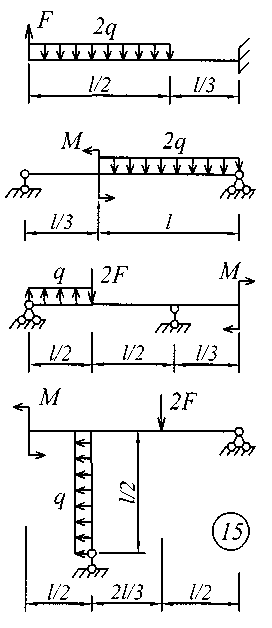
Рис. 3 (окончание) Задание № 4. Построение эпюр внутренних усилий при поперечном изгибе Для четырех заданных расчетных схем стержней требуется: определить опорные реакции; разбить стержень на характерные участки и, пользуясь уравнениями статики, составить аналитические выражения для определения внутренних усилий в произвольном сечении для каждого участка; определить сечения, в которых изгибающий момент имеет экстремальные значения; для каждой схемы построить эпюры внутренних усилий в выбранном масштабе; проверить правильность построения эпюр по дифференциальным зависимостям междуМ, Qиq. Исходные данные для решения этой задачи принять по табл. 4, а расчетные схемы – по рис. 4. Для решения этой задачи необходимо изучить материал, изложенный в [1] – [3], [8], и проанализировать приведенные в этих разделах примеры построения эпюр внутренних усилий. Необходимо запомнить, что инженеры-строители эпюры изгибающих моментов всегда строят только на растянутом волокне! Таблица 4 Исходные данные к заданию № 4
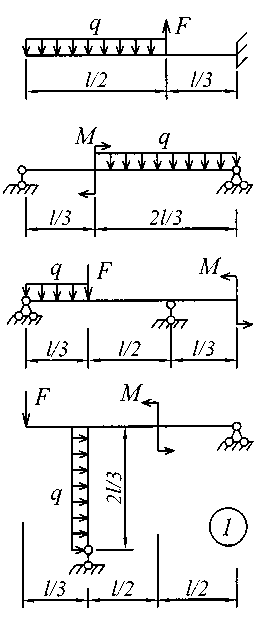
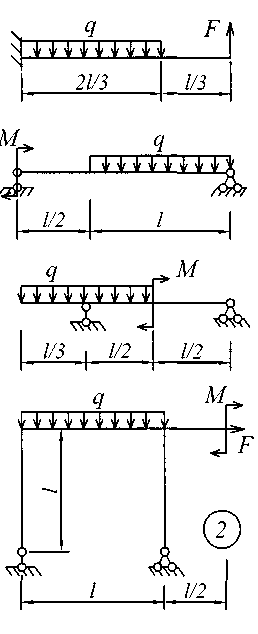
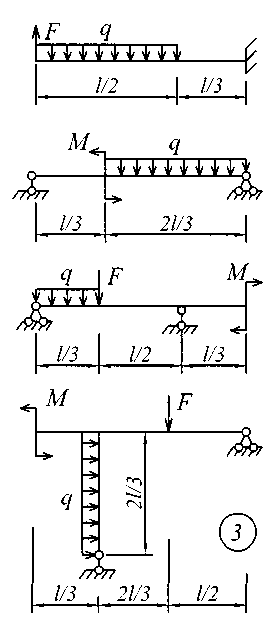
Рис. 4 (начало)
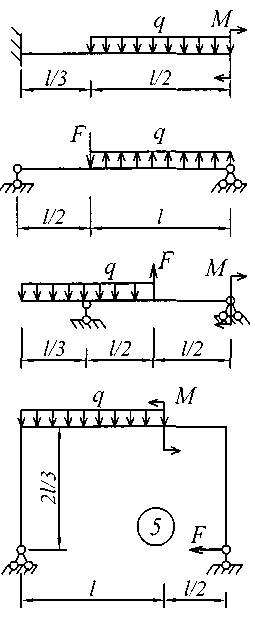
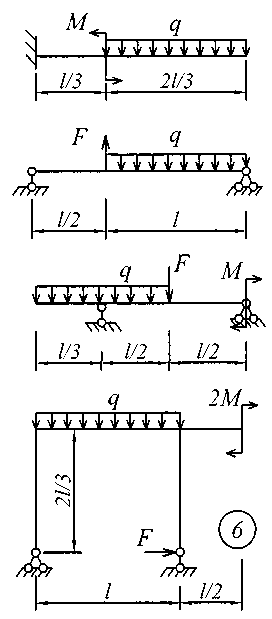
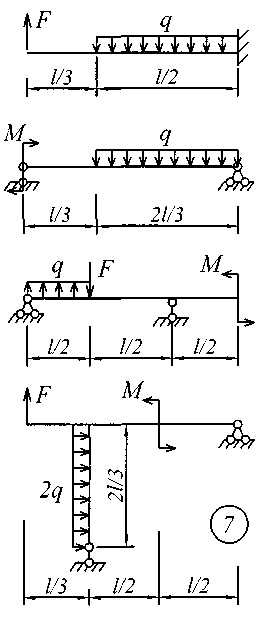
Рис. 4 (продолжение)
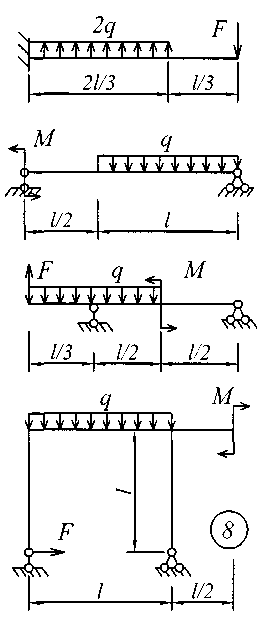
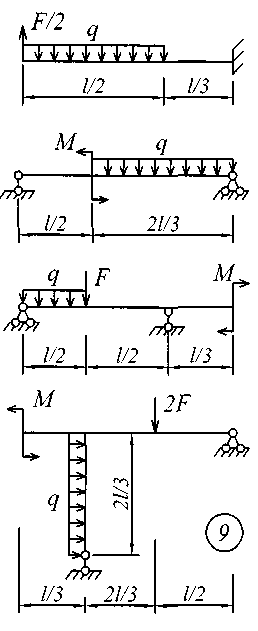
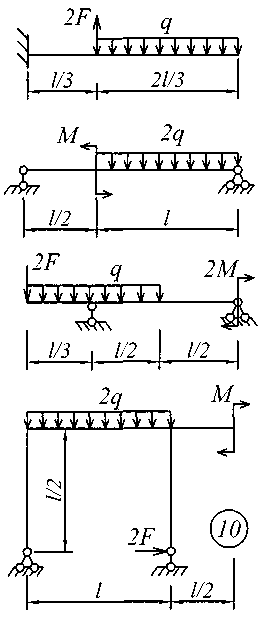
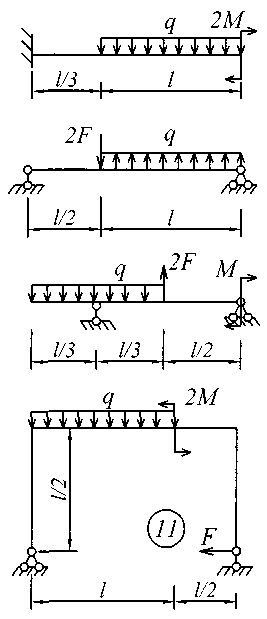
Рис. 4 (окончание) ЗадаНИЕ № 5. Расчеты на прочность и жесткость при поперечном изгибе Для заданной расчетной схемы балки требуется: определить величину и направление опорных реакций; балку разбить на характерные участки, записать аналитические выражения для внутренних усилий на каждом участке, определить усилия в характерных точках каждого участка, построить эпюры внутренних усилий в выбранном масштабе; по экстремальному значению изгибающего момента из условия прочности по нормальным напряжениям назначить размеры поперечного сечения; используя универсальные уравнения метода начальных параметров, определить величины вертикальных перемещений и углов поворота в характерных сечениях балки и построить эпюру прогибов и эпюру углов поворота; по дифференциальным зависимостям проконтролировать правильность построенных эпюр; составить условие жесткости и назначить размеры поперечного сечения из условия жесткости; сравнить размеры поперечного сечения, назначенные из условия прочности и из условия жесткости; установить окончательные размеры поперечного сечения из обоих условий. Для всех вариантов задания принять: поперечное сечение балки двутавровый профиль; расчетные сопротивления стали при изгибе Rи = 200МПа, допускаемый прогиб [f] = L / 300;модуль упругости Е = 2,0610 5 МПа . Остальные исходные данные для решения этой задачи (размеры пролета и значения приложенных к балке нагрузок для всех вариантов задания) приведены в табл. 5; расчетные схемы балок показаны на рис. 5. Таблица 5 Исходные данные к заданию № 5
Для выполнения расчетов на прочность и жесткость при поперечном изгибе необходимо изучить материал, который изложен в учебной литературе [1] – [3], [10].
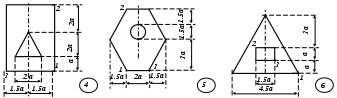
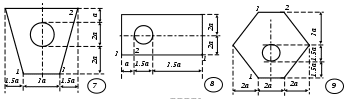
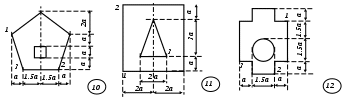
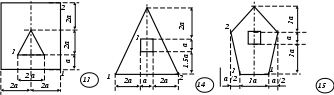
Рис. 5 ЗадаНИЕ № 6. Расчет жесткого бруса на внецентренное сжатие Для заданного поперечного сечения жесткого бруса с известными координатами точки, в которой приложена сжимающая сила F, требуется: определить положение центра тяжести поперечного сечения; определить положение нейтральной линии и показать ее положение в сечении бруса, вычерченном в выбранном масштабе; из условий прочности на сжатие и растяжение найти предельную величину сжимающей силы; при найденной силе определить нормальные напряжения в характерных точках контура сечения и построить эпюру напряжений в изометрической проекции; построить ядро сечения. Исходные данные для решения этой задачи приведены в табл. 6, а расчетные схемы поперечных сечений бруса показаны на рис. 6. Напряженное состояние брусьев при внецентренном приложении нагрузки анализируется в [1] – [3]; теоретические предпосылки и пример расчета изложены в [5]. Таблица 6 Исходные данные к заданию № 6
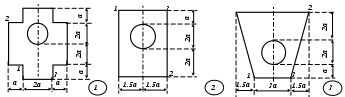
Рис. 6 ЗадаНИЕ № 7. Расчет балки на динамическое действие нагрузки Для заданной расчетной схемы балки, на которую c высоты h падает груз Q, требуется: построить эпюру изгибающих моментов МF от статического действия грузаQ; из условия прочности по нормальным напряжениям назначить размеры поперечного сечения (№ прокатного профиля); методом начальных параметров определить статический прогиб балки в сечении падения груза; определить динамический коэффициент kд (при определении динамического коэффициента массу балки не учитывать); определить величину максимального изгибающего момента с учетом динамического коэффициента и уточнить ранее назначенные размеры сечения балки. Для всех вариантов этой задачи принять модуль упругости материала балки Е = 210 5 МПа, остальные исходные данные для решения приведены в табл. 7; расчетные схемы балок показаны на рис. 7. Таблица 7 Исходные данные к заданию № 7
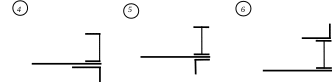
Рис. 7 ЗАДАНИЕ № 8. Расчет сжатого гибкого стержня на устойчивость Для заданной расчетной схемы сжатого однопролетного стержня требуется: из условия устойчивости назначить размеры поперечного сечения равноустойчивой (z = y) двухветвевой стойки (ветви объединены соединительными планками), применяя метод последовательных итераций; установить возможность применения формул Эйлера или Ясинского для определения критической силы; определить величину критической силы по формуле Эйлера или Ясинского; найти коэффициент запаса устойчивости. Для всех вариантов задачи принять: материал стойки – сталь с расчетным сопротивлением R = 240 МПа, модулем упругости Е = 2,06105 МПа тип поперечного сечения – по табл. 8; длину стойки и величину сжимающей силы – по табл. 9, расчетные схемы стоек показаны в табл. 10. Таблица 8 Типы сечений двухветвевых стоек
Таблица 9 Исходные данные к заданию № 8
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






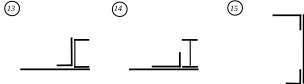
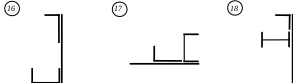
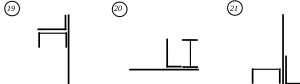
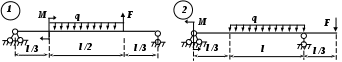
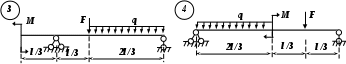
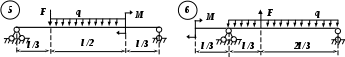
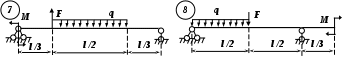
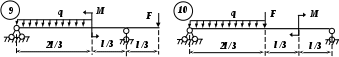
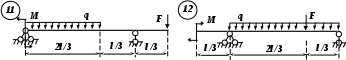
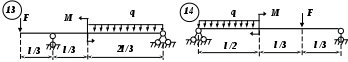
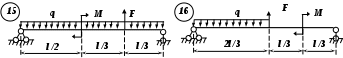

 5
5