сопромуть. Задание Расчет стержня на прочность и

• Название: Задание Расчет стержня на прочность и
• Анкор: сопромуть
• Дата: 16.06.2022
• Размер: 1.13 Mb.
• Имя файла: Sopromat_okonchatelno.doc
• Тип: Конспект; #595911
• страница: 1 из 5

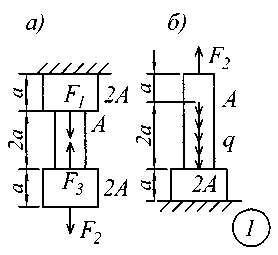
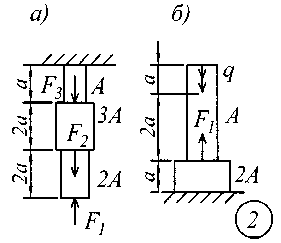
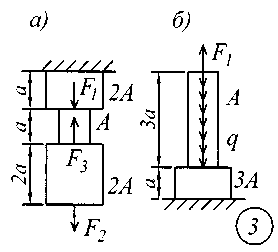
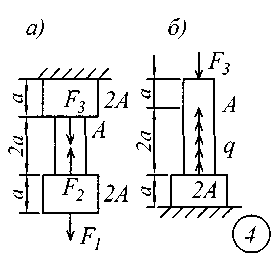
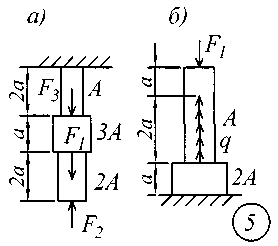
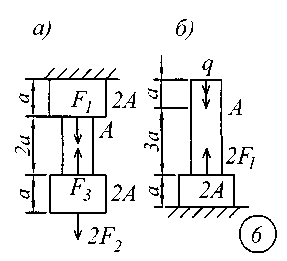
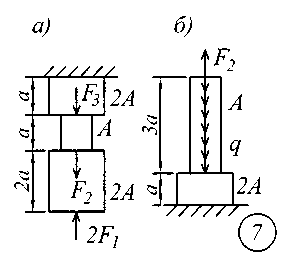
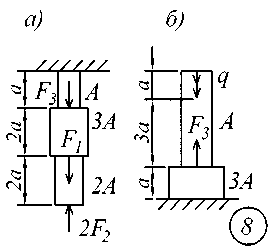
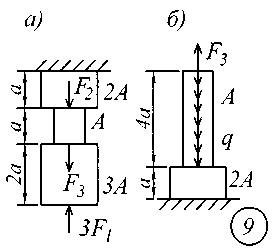
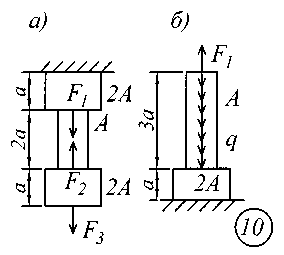
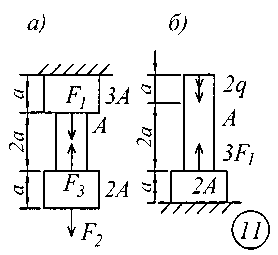
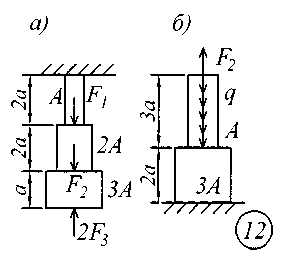
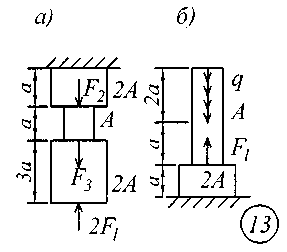
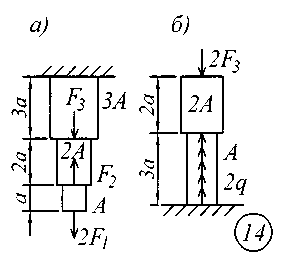
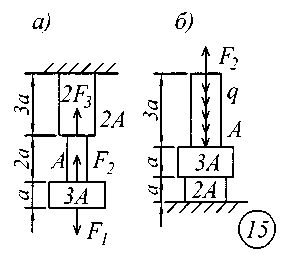
ВВЕДЕНИЕ

Сопротивление материалов – одна из основоположных и трудоемких общетехнических дисциплин, изучаемых в вузе, поэтому занятия по курсу должны обязательно сопровождаться составлением конспекта и решением задач.

Если при решении задачи возникают трудности, следует обратиться к примерам и указаниям, приведенным в литературе, рекомендованной для изучения рассматриваемого раздела. При этом следует обращать особое внимание на физическую сущность рассматриваемого явления и на те допущения и ограничения, которые делаются в процессе выводов.

Задание № 1. Расчет стержня на прочность и

жесткость при осевом действии нагрузок
К ступенчатому стержню приложены продольные внешние воздействия: сосредоточенные силы Fи распределенная нагрузка интенсивностью q.

Для всех вариантов этой задачи принять:

- расчетное сопротивление материала R = 200МПа;

- нормативное удлинение (укорочение) участка стержня [l]= а / 500;

- модуль упругости материала Е = 2,0610⁵ МПа.

Требуется:

1. 
   начиная с незакрепленного края стержня, разбить его на характерные участки в зависимости от схемы приложения нагрузок и изменения поперечного сечения;
   
2. 
   записать аналитические выражения для определения внутренних усилий на каждом участке, рассчитать их величину в характерных точках и построить их эпюру;
   
3. 
   определить величину нормальных напряжений, выраженную через площадь А на каждом участке и построить их эпюру ( эп. );
   
4. 
   исходя из условия прочности в опасном сечении, определить площадь А поперечного сечения стержня;
   
5. 
   с учетом найденного значения площади А найти величину продольных деформаций для каждого участка и построить эпюру перемещений (эп. а);
   
6. 
   по полученным данным оценить жесткость стержня.
   

Расчетные схемы стержней показаны на рис.1, а исходные данные для решения задачи приведены в табл. 1. Теоретический материал и примеры расчетов на осевое действие нагрузок приводятся в [1] – [4], [6], [8].


Рис. 1

Таблица 1

Исходные данные к заданию № 1

Номер строки	F1 , кН	F2 , кН	F3 , кН	q, кН/м	а, м
1	15	12	18	45	0.30
2	10	15	20	40	0.40
3	20	14	8	30	0.35
4	8	16	10	20	0.50
5	30	10	12	40	0.55
6	12	8	15	25	0.60
7	14	20	10	40	0.45
8	15	10	12	25	0.70
9	20	15	15	30	0.55
10	16	10	12	15	0.80
11	18	12	10	30	0.65
12	22	10	15	20	0.75
13	30	12	18	35	0.40
14	35	20	10	50	0.55
15	10	25	30	30	0.50

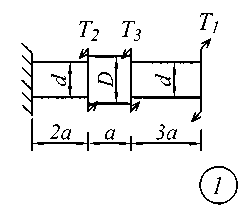
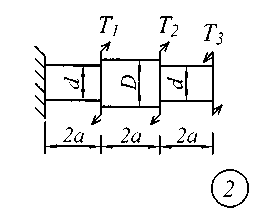
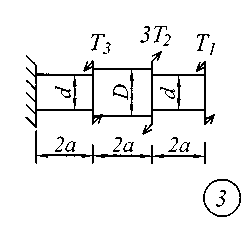
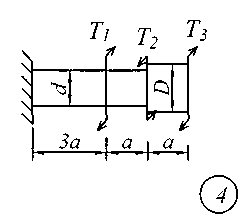
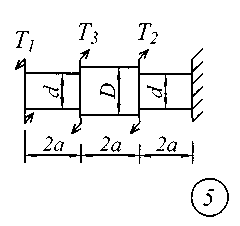
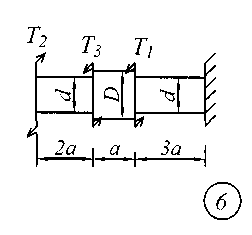
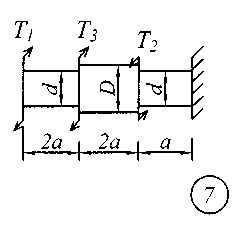
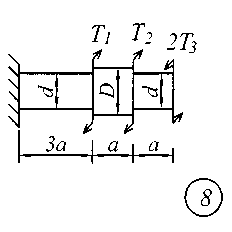
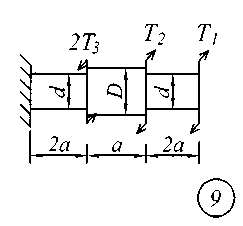
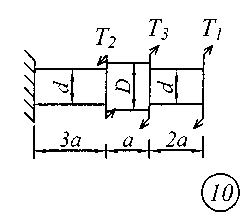
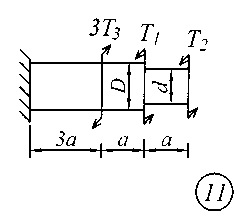
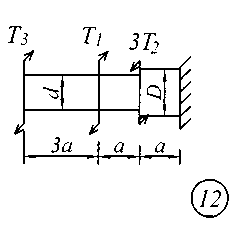
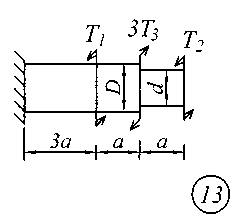
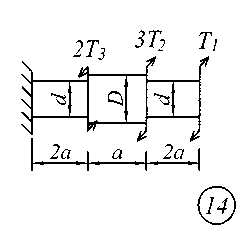
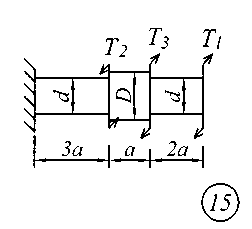
Задание № 2. Расчет стержня на прочность

и жесткость при кручении
Ступенчатый брус с круглым поперечным сечением нагружен сосредоточенными крутящими моментами Т. Материал  сталь с расчетным сопротивлением на сдвиг R_s = 130 МПа.Нормативный угол закручивания []=0,5 ⁰; G = 0,8 10 ⁵ МПа.

Требуется:

1. 
   начиная с незакрепленного края стержня, записать аналитические выражения для определения внутренних усилий для каждого участка рассчитываемого вала, определить их величину в характерных точках и построить эпюру крутящих моментов (эп. Т, кНм );
   
2. 
   исходя из соотношения D = 1.2d, определить величину касательных напряжений в характерных точках каждого участка и построить эпюру напряжений (эп. ), выраженную через диаметр d;
   
3. 
   исходя из условия прочности при кручении в опасном сечении, определить диаметр бруса на каждом участке;
   
4. 
   определить величину угловых деформаций на каждом участке и построить эпюру углов закручивания (эп. , рад);
   
5. 
   по полученным данным оценить жесткость вала.
   

Исходные данные для решения задачи приведены в табл. 2, расчетные схемы показаны на рис. 2.


Рис. 2

Таблица 2

Исходные данные к заданию № 2

Номер строки	Т1 , кНм	Т2 , кНм	Т3 , кНм	а, м
1	2	5	4	0.50
2	4	7	6	0.40
3	6	9	2	0.35
4	8	3	3	0.60
5	10	1	5	0.70
6	3	8	1	0.40
7	5	6	8	0.55
8	7	4	9	0.80
9	9	2	7	0.25
10	1	8	3	0.30
11	4	5	6	0.65
12	7	6	2	0.20
13	2	7	8	0.45
14	5	6	9	0.15
15	8	9	4	0.25
16	8	2	3	0.65
17	11	4	2	0.20
18	6	7	9	0.25
19	7	5	2	0.45
20	13	9	5	0.40
21	9	10	4	0.35

Определение внутренних усилий в сечениях и методика расчета валов с круглым поперечным сечением на прочность и жесткость приводятся в [1] – [4], [6], [8].


Задание № 3. Определение геометрических

характеристик плоских сечений
Задано сечение, составленное из двух элементов прокатного профиля и листа.

Требуется:

1. 
   определить положение центра тяжести сечения;
   
2. 
   вычислить осевые и центробежный моменты инерции сечения относительно центральных осей;
   
3. 
   определить положение главных центральных осей инерции сечения;
   
4. 
   вычислить величину главных центральных моментов инерции сечения;
   
5. 
   вычертить в масштабе 1:1 или 1:2 сечение, показать все необходимые оси с указанием расстояний между ними и всеми размерами элементов, входящими в состав сечения;
   
6. 
   построить эллипс инерции.
   

Исходные данные для решения задачи следует принять по табл. 3, а расчетную схему сечения  по рис. 3.
Таблица 3