КР+ПРАКТ_alena_suhova. Задание 1
 Скачать 288.35 Kb. Скачать 288.35 Kb.
|
|
Задача 1. Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов. Решение: 1) Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе, определяется по формуле средней арифметической взвешенной: 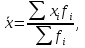 где xi 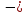 удельный вес студентов ВУЗов, обучающихся на коммерческой основе; удельный вес студентов ВУЗов, обучающихся на коммерческой основе;fi 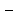 число студентов ВУЗов. число студентов ВУЗов.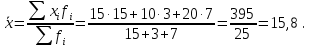 2) Число этих студентов ВУЗов, обучающихся на коммерческой основе Поскольку количество студентов, обучающихся на коммерческой основе, занимает небольшой удельный вес, запишем общее количество студентов не в тысячах, а в единицах (человек). Таблица – Расчет числа студентов ВУЗов, обучающихся на коммерческой основе
Общее число студентов ВУЗов, обучающихся на коммерческой основе равняется: 2250+300+1400=3950 чел. Задача 1 При изучении влияния рекламы на размер среднемесячного вклада в банках района обследовано 2 банка. Получены следующие результаты:
Определить:
Таблица 1.1 - Данные для расчетов всех видов дисперсий
а) Средний размер вклада за месяц для каждой группы банков находим по формуле средней арифметической взвешенной 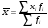 где хi - значения осредняемого признака; fi - веса. Группа банков с рекламой: 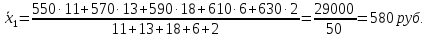 Группа банков без рекламы: 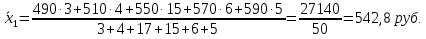 б) Дисперсия групповая: Групповую (частную) дисперсию размера вкладов по каждой группе банков определяем по формуле: 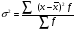 Группа банков с рекламой
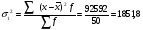 Группа банков без рекламы
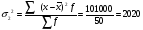 2. Средний размер вклада за месяц для двух банков вместе: 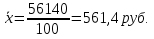 3. Дисперсия вклада для 2-х банков, зависящая от рекламы
Дисперсия вклада для 2-х банков, зависящая от рекламы 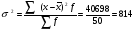 4) Дисперсия вклада для 2-х банков, зависящая от всех факторов, кроме рекламы
Дисперсия вклада для 2-х банков, зависящая от всех факторов, кроме рекламы 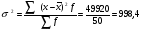 5) находим общую дисперсию по правилу сложения дисперсий: 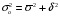 , ,где 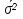 - средняя из внутригрупповых дисперсий; - средняя из внутригрупповых дисперсий;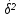 - межгрупповая дисперсия. - межгрупповая дисперсия.Вычисляем среднюю из внутригрупповых дисперсий: 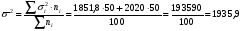 . .Определяем межгрупповую дисперсию:
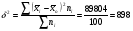 Общая дисперсия: 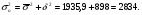 6) Коэффициент детерминации определяется по формуле 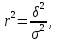 где - общая дисперсия;- межгрупповая дисперсия. где - общая дисперсия;- межгрупповая дисперсия.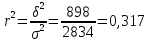 7) Эмпирическое корреляционное отношение рассчитываем по формуле: 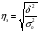 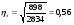 Полученное эмпирическое корреляционное отношение свидетельствует о том, что связь между признаками заметная. Размер вкладов в банках на 56% зависит от количества вкладчиков в банках. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

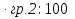
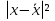
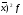
 3=24300
3=24300 4=19600
4=19600