КР+ПРАКТ_alena_suhova. Задание 1
 Скачать 288.35 Kb. Скачать 288.35 Kb.
|
|
Задание 1 Вариант 4 с Определите индивидуальные и общие индексы: физического объема, цены, стоимости (или товарооборота); абсолютные изменения данных показателей. Сделайте вывод.
Решение:
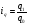 , где , где 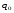 , , 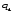 – объем продукции определенного вида в натуральном выражении соответственно в 1 и 2 квартале; – объем продукции определенного вида в натуральном выражении соответственно в 1 и 2 квартале;
Вывод: Количество реализации продукции во втором квартале по сравнению с первым кварталом увеличилось по продукции А на 7,1%, или на 4 тыс. м; по продукции В на – 15,8%., или на 6 тыс. шт.; по продукции D – на 1,8% или на 2 тыс. кв. м. Уменьшение количества реализации продукции во втором квартале по сравнению с первым кварталом произошло по продукции С на 10,6% или на 5 тыс. кг; и по продукции F на 5,1% или на 15 тыс. л. 2) Индивидуальный индекс цены одного вида продукции вычисляем по формуле: 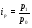 где 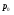 , , 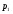 – цена единицы продукции конкретного вида соответственно в 1 и 2 квартале. – цена единицы продукции конкретного вида соответственно в 1 и 2 квартале.
Вывод: Цена единицы продукции во втором квартале по сравнению с первым кварталом снизилась по продукции В на 5,9% ; по продукции D на – 2,6%; и по продукции F – на 2,2% или на 2 денежных. ед. по каждому виду продукции (34-32=-2 и т.д. аналогично). Рост цен во втором квартале по сравнению с первым кварталом произошел по продукции А на 36,4% или на 4 денежных ед. и по продукции С на 16,1% или на 9 денежных единиц. 3) Индивидуальный индекс товарооборота вычисляем по формуле: 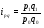 где p0q0 – товарооборот за первый квартал; p1q1 – товарооборот за второй квартал.
Вывод: Товарооборот (стоимость реализованной продукции) во втором квартале по сравнению с первым кварталом по трем видам продукции А, В и С увеличился: по продукции А на 46,1% или на 284 тыс. денежных. ед.; по продукции В на 9,0% или на 116 тыс. денежных ед., по продукции С на 3,7% или на 98,0 тыс. денежных ед. По продукции D товарооборот снизился на 0,8% или на 66 тыс. денежных ед. и по продукции F снизился на 7,2% или на 1910 тыс. денежных ед. 4) Для определения общих индексов расчетные данные заполним в таблице 1.1. Таблица 1.1 – Расчетные данные для определения общих индексов
Общий индекс физического объема товарооборота определяется по формуле:  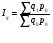 ; ;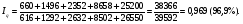 Физический объем (количество продукции), в среднем по всем видам продукции во втором квартале по сравнению с первым кварталом, уменьшился на 3,1%. Общий индекс цен определяется по формуле: 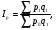 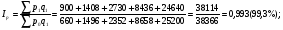 Цены, в среднем по всем видам продукции во втором квартале по сравнению с первым кварталом, снизилась на 0,7%. Общий индекс товарооборота определяется по формуле: 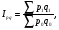 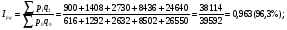 Товарооборот, в среднем по всем видам продукции во втором квартале по сравнению с первым кварталом, снизился на 3,7%. Абсолютное изменение товарооборота во втором квартале по сравнению с первым кварталом составляет: 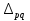 = =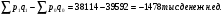 В том числе: Абсолютное изменение товарооборота в результате изменения цен:  = =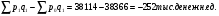 Абсолютное изменение товарооборота в результате изменения физического объема продукции: 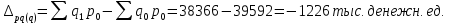 Снижение товарооборота на 1478 тыс. денежных ед. произошло за счет уменьшения количества реализованной продукции на 1226 тыс. денежных единиц и снижения цен на 252 тыс. денежных ед. 2. Вариант под буквой "С" Уровень использования среднегодовой производственной мощности организаций по выпуску отдельных видов продукции1) (в процентах)
Данные Росстата. Необходимо спрогнозировать изменение использования среднегодовой мощности организаций по производству пищевых продуктов по водам минеральным на 2010-2013 гг. методом составления уравнения линейной регрессии. Решение: Линейное уравнение тренда имеет вид: 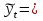 a0 + a1t. a0 + a1t.где : 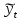 – выравненные (теоретические) уровни ряда динамики; – выравненные (теоретические) уровни ряда динамики;t – время, то есть порядковые номера периодов времени (годы); а0 , а1 – параметры уравнения: а0 – начало отсчета; а1 – коэффициент регрессии или пропорциональности, который показывает средний ежегодный прирост (снижение) в частности изменение использования среднегодовой мощности по производству минеральных вод. Находим параметры уравнения методом наименьших квадратов. Система уравнений имеет вид: a0n + a1∑t = ∑y a0∑t + a1∑t2 = ∑y  t tТаблица 1 – Расчетные данные для выравнивания ряда динамики по линейному тренду
Для наших данных система уравнений имеет вид: a0 9+ a145= 489 a0 15+ a1 55= 2379 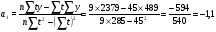 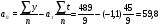 Получаем a0 = 59,8; a1 =-1,1. Уравнение тренда: 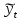 = a0 + a1t = a0 + a1t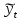 = 59,8 + (-1,1) t = 59,8 + (-1,1) tДля 2010 года (10 период) значение тренда рассчитывается по следующей схеме: в уравнение подставляем t=10 и получаем y = 59,8 + (-1,1·10)=48,8%. Для 2011 года (11 период) значение тренда рассчитывается по следующей схеме: в уравнение подставляем t=11 и получаем y = 59,8 + (-1,1·11)=47,7%. Для 2012 года (12 период) значение тренда рассчитывается по следующей схеме: в уравнение подставляем t=12 и получаем y = 59,8 + (-1,1·12)=46,6%. Для 2013 года (13 период) значение тренда рассчитывается по следующей схеме: в уравнение подставляем t=13 и получаем y = 59,8 + (-1,1·13)=42,2%. Таким образом, прогнозируем уровень использования среднегодовой производственной мощности организаций по выпуску минеральных вод на 2010 год 48,8%, на 2011 г. – 47,7%, на 2012 г. – 46,6%, на 2013 г. – 42,2. 3. Вариант под буквой "С" ДЕНЕЖНО - КРЕДИТНАЯ СИСТЕМА ДЕЯТЕЛЬНОСТЬ СТРАХОВЫХ ОРГАНИЗАЦИЙ 1)
1) Приведены данные по страховым организациям, зарегистрированным в Свердловской области
Решение: 1.Определяем показатели динамического ряда на цепной и базисной основе. Цепной способ – сравнение каждого уровня с предыдущим уровнем. Абсолютный прирост определяется по формуле: 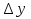 = = 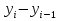 1505,6 –1714,7 = –209,1 тыс. единиц; 1649,8–1505,6 = 144,2 тыс. единиц; 1549,5 –1649,8 = –100,3 тыс. единиц; 1274,2 –1549,5 = –275,3 тыс. единиц. Темп роста определяется по формуле: Тр = 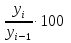 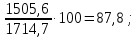 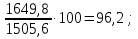 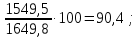 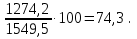 Темп прироста определяется по формуле: Тпр = Тр – 100% 87,8 –100,0 = –12,2% ; 96,2 – 100,0 = 9,6%; 90,4 –100,0 = –6,1% ; 74,3 – 100,0 = –17,8. Базисный способ – сравнение каждого уровня с базой сравнения. За базу сравнения берется I уровень, т.е. 2003 год. Абсолютный прирост определяется по формуле: 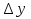 = = 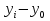 . . 1505,6 –1714,7 = –209,1 тыс. единиц; 1649,8–1714,7 = -64,9 тыс. единиц; 1549,5 –1714,7 = –165,2 тыс. единиц; 1274,2 –1714,7 = –440,5 тыс. единиц. Темп роста определяется по формуле: Тр = 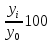 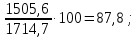 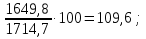 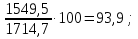 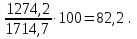 Темп прироста определяется по формуле: Тпр = Тр – 100% 87,8 –100,0 = –12,2% ; 109,6 – 100,0 = –3,8%; 93,9 –100,0 = –9,6%; 82,2 – 100,0 = –25,7% . Абсолютное значение 1% прироста определяем по цепным показателям как отношение 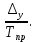 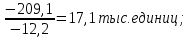 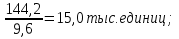 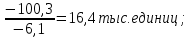 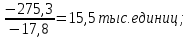 Результаты расчетов представлены в таблице 1. Таблица 1  Аналитические показатели динамики числа заключенных договоров страхования Аналитические показатели динамики числа заключенных договоров страхования
Среднегодовое число заключенных договоров страхования определяется по формуле средней арифметической простой (для интервального ряда динамики): 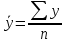 , ,где 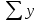 – сумма уровней ряда; n – число уровней ряда (количество лет). – сумма уровней ряда; n – число уровней ряда (количество лет).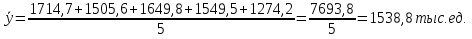 3. Среднегодовой темп роста (снижения) равен 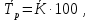 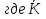 - среднегодовой коэффициент роста (снижения ) - среднегодовой коэффициент роста (снижения )Среднегодовой коэффициент роста (снижения) может быть исчислен на базе ежегодных коэффициентов роста (снижения) по формуле средней геометрической 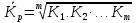 , ,где m – число коэффициентов. 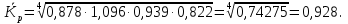 Коэффициенты роста исчислены из цепных темпов роста: 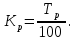 Среднегодовой коэффициент роста (снижения) может быть исчислен также на базе абсолютных показателей ряда динамики по формуле: 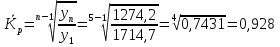 n– число уровней ряда; (n – 1)– число лет; 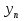 – последний уровень ряда; – последний уровень ряда;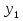 – первый уровень ряда. – первый уровень ряда.Среднегодовой темп роста (снижения) равен: 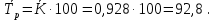 Среднегодовой темп прироста (снижения) определяется путем вычитания из среднегодового темпа роста 100%. В нашем примере среднегодовой темп снижения равен: 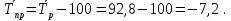 Средний абсолютный прирост исчисляется по формуле средней арифметической простой: 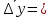 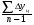 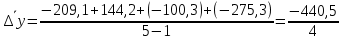 =-110,1 тыс. единиц. =-110,1 тыс. единиц.Прогнозирование числа заключенных договоров страхования на 2008 год с помощью среднего абсолютного прироста: Расчетный уровень динамического ряда на любую дату yt определяется по формуле: 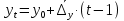 где y0 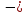 начальный уровень ряда; начальный уровень ряда;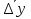 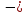 средний абсолютный прирост; средний абсолютный прирост;t 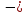 порядковый номер даты (года); порядковый номер даты (года);Уровень динамического ряда на 2008 год (6 период) 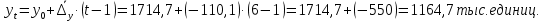 Прогнозирование числа заключенных договоров страхования на 2008 год с помощью среднего темпа роста:
где K 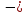 средний темп роста. средний темп роста.Прогноз на 2008 год (6 период) yt = 1714,7 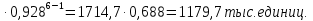 Выводы: На протяжении 2003-2007 гг. наблюдается динамика снижения числа заключенных договоров страхования. Только в 2005 г. по сравнению с 2004 г. количество заключенных договоров страхования увеличивается на 144,2 тыс. единиц или на 9,6%, хотя по сравнению с 2003 годом, взятым за базу сравнения, этот показатель снижается на 3,8%. В 2007 г. происходит максимальное снижение показателя на 275,3 тыс. единиц договоров, или на 17,8%. Среднегодовое число заключенных договоров страхования составляет 1538,8 тыс. единиц. Среднегодовой темп роста составляет 92,8%., соответственно среднегодовой темп снижения 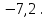 Абсолютное снижение числа заключенных договоров в среднем за год составляет 110,1 тысяч. Предполагая, что выявленная закономерность сохранится и в дальнейшем, спрогнозировано число заключенных договоров страхования на 2008 год: с помощью среднего темпа роста прогнозное число договоров страхования составляет 1179,7тысяч, и с помощью среднего абсолютного прироста - 1164,7тыс. единиц. 4. Задача 3.5. Крестьянские хозяйства подразделяются по размерам земельных угодий следующим образом;
Рассчитайте:
Сделать выводы. Решение: Для проведения расчетов необходимо определить середину интервала по каждой группе, например, для второго интервала 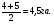 и т.д. На первый открытый интервал распространим размер соседнего интервала (5-4=1) и тогда будем считать интервал от 2 до 3, и его середина – 2,5. Аналогично определим границу по последнему интервалу: 200-101=99; 201+99=300. Размер последнего интервала 201- 300. и т.д. На первый открытый интервал распространим размер соседнего интервала (5-4=1) и тогда будем считать интервал от 2 до 3, и его середина – 2,5. Аналогично определим границу по последнему интервалу: 200-101=99; 201+99=300. Размер последнего интервала 201- 300.Для определения показателей вариации построим вспомогательную таблицу 4.1. Таблица 4.1 – Расчетные данные для определения показателей вариации
Средний размер земельных угодий хозяйств, поставляющих продукцию только высшего и первого сорта, определяем по формуле средней арифметической взвешенной 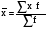 Значения суммы xf и суммы f берем в итоговой графе таблицы и подставляем в формулу 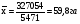 Таким образом, средний размер земельных угодий хозяйств, поставляющих продукцию только высшего и первого сорта, составляет 59,8 га. Этот показатель используем при расчете гр.5. Результаты расчетов проставляем без учета знаков +, 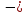 . .Размах вариации R=xmax –xmin =300 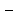 2 = 208 га. 2 = 208 га.Среднее линейное отклонение определяется по формуле: d= 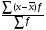
Аналогично проведены все расчеты и отображены во вспомогательной таблице. d= 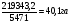 Среднее квадратическое отклонение определяется по формуле: 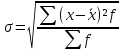 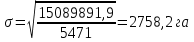 Это означает, что на 2758,2 га в среднем отклоняются индивидуальные значения земельных угодий от их среднего значения, которое составляет 59,8 га. Отклонение очень значительное. Коэффициент вариации равен 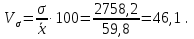 Такой высокий процент (˃33%) говорит о большой колеблемости совокупности крестьянских хозяйств по размеру земельных угодий. То есть совокупность является неоднородной и средний размер земельных угодий не типичный для данной совокупности. Таблица 4.2 – Расчетные данные для определения моды и медианы
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

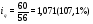 .
.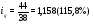 .
.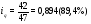 .
.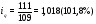 .
.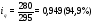 .
.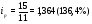 .
.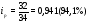 .
.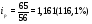 .
.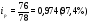
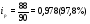 .
.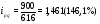 .
.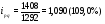 .
.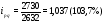 .
.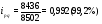 .
.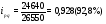
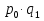
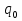
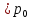
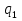
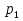
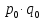
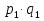
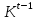 ,
,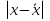
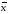 )f
)f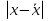
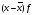
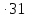 =1776,3
=1776,3