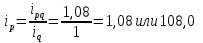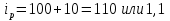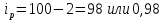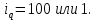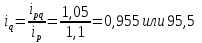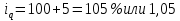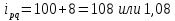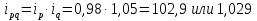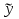КР+ПРАКТ_alena_suhova. Задание 1
 Скачать 288.35 Kb. Скачать 288.35 Kb.
|
|
Задача 1. Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:
Определить: 1) по предприятиям, включенным в выборку: а) средний размер произведенной продукции на одно предприятие; б) дисперсию объема производства; в) долю предприятий с объемом производства продукции более 400 тыс. руб.; 2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать: а) средний объем производства продукции на одно предприятие; б) долю предприятий с объемом производства продукции более 400 тыс. руб.; 3) общий объем выпуска продукции по области. Решение: Для определения среднего размера и дисперсии необходимо определить середину интервала по каждой группе, например, для второго интервала 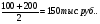 и т.д. На первый открытый интервал распространим размер соседнего интервала (200 – 100 =100) и тогда будем считать интервал от 0 до 100, и его середина – 50. Аналогично определим границу по последнему интервалу. и т.д. На первый открытый интервал распространим размер соседнего интервала (200 – 100 =100) и тогда будем считать интервал от 0 до 100, и его середина – 50. Аналогично определим границу по последнему интервалу.По исходным данным составим таблицу для проведения расчетов. Таблица 1.1 – Расчетные данные для определения среднего объема продукции и дисперсии
1. а) Cредний размер произведенной продукции на одно предприятие определяем по формуле средней арифметической взвешенной: 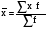 Значения суммы xf и суммы f берем в итоговой графе таблицы и подставляем в формулу 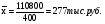 Таким образом, cредний размер произведенной продукции на одно предприятие составляет 277 тыс. руб. Этот показатель используем при расчете гр.5. Результаты расчетов проставляем без учета знаков +, 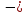 . .б) Дисперсия определяется по формуле: 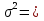 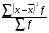 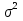 = = 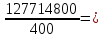 319287 . 319287 .в) Доля предприятий с объемом производства продукции более 400 тыс. руб. w= 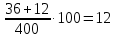 . .2. a) С вероятностью 0,954 определяем предельную ошибку выборочной средней и возможные границы, в которых ожидается средний объем производства продукции на одно предприятие. Предельная ошибка признака равна 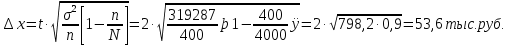 где N – генеральная совокупность (4000 при 10% выборке); n – выборочная совокупность (400 предприятий); t – коэффициент доверия, при вероятности 0,954 равняется 2. Определим возможные границы, в которых ожидается средний объем производства продукции на одно предприятие: 277 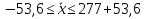 или 223,4 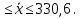 Следовательно, с вероятностью 0,954 можно утверждать, что средний объем производства продукции на одно предприятие в генеральной совокупности находится в пределах от 223,4 до 330,6 тыс. руб. б) С вероятностью 0,954 определяем предельную ошибку выборочной доли и возможные границы, удельного веса предприятий с объемом производства продукции более 400 тыс. руб. Доля предприятий с объемом производства продукции более 400 тыс. руб. составляет 12%. Предельная ошибка доли равна: 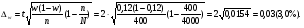 Пределы доли признака в генеральной совокупности: 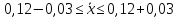 или 0,09 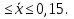 Таким образом, с вероятностью 0,954 можно утверждать, что доля предприятий с объемом производства продукции более 400 тыс. руб. находится в пределах от 9 % до 15%. 3) Объем выпуска продукции по выборочной совокупности составляет  110800 тыс. руб. (см. таблицу 1.1 гр.4). 110800 тыс. руб. (см. таблицу 1.1 гр.4).Общий объем выпуска продукции по области 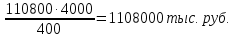 Задача1. Данные о площадях под картофелем до и после изменения границ района, тысяч гектаров:
Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района. Решение: Таблица – Площадь под картофелем в условиях изменения границ района, тыс. га
Задача 1. По нижеприведенным данным ответить на вопросы, поставленные в таблице, т.е. определить недостающие показатели.
Решение: Недостающие показатели можно определить исходя из взаимосвязи индексов, а именно: индекс товарооборота равняется произведению индексов цены и натурального объема продаж 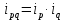
Цена во II квартале увеличилась на 8,0%. Натуральный объем продаж в III квартале снизился на 4,5%. Товарооборот в денежном выражении в IV квартале увеличился на 2,9%. Заполним таблицу с исходящими данными и недостающими показателями.
Задача 1. По пяти рабочим цеха имеются данные о квалификации и месячной выработке. Для изучения связи между квалификацией рабочих и их выработкой определить линейное уравнение связи и коэффициент корреляции. Дать интерпретацию коэффициентам регрессии и корреляции.
Решение Уравнение линейной регрессии, выражающее взаимосвязь между между квалификацией рабочих и их выработкой: 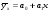 Рассчитать параметры уравнения регрессии по методу наименьших квадратов можно, используя следующую систему нормальных уравнений: 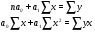 , ,где 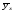 – теоретические значения выработки продукции за смену; – теоретические значения выработки продукции за смену;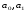 – параметры уравнения регрессии; – параметры уравнения регрессии;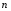 – число единиц наблюдения (рабочих). – число единиц наблюдения (рабочих).Решение указанной системы уравнений дает следующие формулы для нахождения параметров 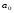 и и 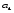 : :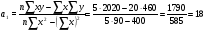 ; ;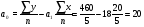 Параметр 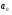 показывает, сколько составила бы выработка продукции за смену, при отсутствии влияния квалификации рабочего. Выработка продукции за смену составила бы 20шт. показывает, сколько составила бы выработка продукции за смену, при отсутствии влияния квалификации рабочего. Выработка продукции за смену составила бы 20шт.Показатель а1 означает, что при увеличении тарифного разряда на 1единицу выработка продукции увеличится на 18 шт. Расчетные данные для определения теоретического значения выработки продукции за смену
Сумма теоретических значений выработки продукции за смену совпадает с фактической выработкой продукции. Коэффициент корреляции r определим по формуле: 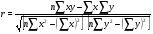 . .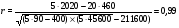 Показатель 0,99 свидетельствует о весьма высокойтесноте связи между квалификацией рабочих и их выработкой. Коэффициент детерминации r2 = 0,992 =0,98 Коэффициент детерминации показывает, что на 98% вариации полученной выработки продукции за смену зависит от вариации квалификации рабочих и только на 2% от других факторов. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

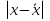
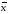 )2
)2