Санкт-Петербург
2021
вмваиавиуауауаув Задание №12222333333R2R4543543efe4234234234wwуауауe2435345345345eifjwiefu89wefu8ew4wegwegwegw3232332wwwqqуауаqwwwsdsdsddsdsуауауregergregergreg
Спроектировать, реализовать и провесуауати тестовые испытания АТД «BST – дерево» для коллекции, содержащей данные произвольного типа. Тип коллекции задаётся клиентской программой.
Интерфейс АТД «BST – дерево» включает следующие операции:
опрос размера дерева,
очистка дерева,
проверка дерева на пустоту,
поиск объекта с заданным ключом,
включение нового объекта с заданным ключом,
удаление объекта с заданным ключом,
обход объектов в дереве по схеме, заданной в варианте задания,
дополнительная операция, заданная в варианте задания.
Для тестирования коллекции интерфейс АТД «BST – дерево» включает дополнительные операции:
вывод структуры дерева на экран,
опрос числа просмотренных операцией узлов дерева.
Выполнить отладку и тестирование всех операций АТД «BST – дерево» с помощью меню операций.
Выполнить тестирование средней трудоёмкости операций поиска, вставки и удаления элементов для среднего и худшего случаев.
Провести сравнительный анализ экспериментальных показателей трудоёмкости операций.
Составить отчёт. Отчёт должен содержать следующие пункты:
титульный лист,
общее задание (пункты 1 – 4) и вариант задания,
формат АТД,
определение класса для коллекции «BST – дерево»,
описание методики тестирования трудоёмкости операций,
описание методики тестирования трудоёмкости операций,
таблицы и графики с полученными оценками трудоёмкости операций для худшего и среднего случаев функционирования АТД. Должны быть приведены графики среднего числа пройденных узлов для операций поиска, вставки и удаления (графики совмещены в одной системе координат),
выводы,
список использованной литературы,
приложение с текстами программ:
Алгоритмы операций АТД реализуются в рекурсивной форме.
Схема операции обхода: Схема операции обхода: Lt → t → Rt.
Дополнительная операция: определение критерия сбалансированности для узлов дерева.
Формат АТД «Двоичное дерево поиска» (BST):
Двоичное дерево поиска. Дерево представляет собой связную структуру данных, связь между элементами которой имеет вид – правый и левый потомки.
Данные:
Двоичное дерево поиска на базе адресных указателей.
Единица хранимых данных объединяет ключ key и данные data.
Данные в дереве упорядочиваются по ключу.
size – размер дерева.
Операции:
Конструктор:
Вход: Нет
Начальные значения: Нет
Процесс: Создание дерева
Постусловия: Дерево создано, size=0
Конструктор копирования
Вход:Копируемое дерево
Начальные значения:Нет
Процесс:Создание копии дерева
Постусловия:Дерево создано.
Опрос размера дерева:
Вход: Нет
Предусловия: Нет
Процесс: Нет
Выход: Размер дерева size
Постусловия: Нет
Очистка дерева:
Вход: Нет
Предусловия: Нет
Процесс: Очистка дерева
Выход: Нет
Постусловия: Дерево пустое. size=0
Добавление нового узла в дерево:
Вход: Ключ key и данные data для добавления
Предусловия: Узла с ключом key еще нет в дереве
Процесс: Добавление нового узла в дерево
Выход: True/False
Постусловие: В дерево добавлен новый узел. size= size+1
Удаление узла из дерева:
Вход: Ключ key удаляемого узла.
Предусловия: В дереве имеется узел с ключомkey
Процесс: Удаление из дерева узла с ключомkey
Выход: True/False
Постусловие: Из дерева удален узел. size= size-1
Поиск данных с заданным ключом:
Вход: Ключ для поиска – key
Предусловия: В дереве имеется узел с ключомkey
Процесс: Получение данных по заданному ключу
Выход: Найденные данные/Ошибка
Постусловие: Нет
Обход дерева по схеме Lt – t – Rt:
Вход: функция для выполнения
Предусловия: нет
Процесс: обход дерева по схеме Lt – t – Rt, с выполнением для каждого узла заданной программы, в которую в качестве аргумента передается ключ текущего узла
Выход: нет
Постусловие: для ключей каждого элемента в дереве выполнена заданная функция
АТД «Итератор»
Итератор позволяет перемещаться по объектам коллекции и получать к ним доступ.
Имеет статус – в дереве(Указывает на узел)/вне дерева(Не указывает)
Операции:
Конструктор:
Вход: Двоичное дерево поиска
Начальные значения: Нет
Процесс: Создание итератора
Постусловия: Итератор создан
Установка на начало:
Вход: Нет
Предусловия: В дереве есть хотя бы один узел
Процесс: Перемещение итератора на узел дерева с минимальным ключом
Выход: True/False
Постусловия: Итератор установлен на узел дерева с минимальным ключом
Установка на конец:
Вход: Нет
Предусловия: В дереве есть хотя бы один узел
Процесс: Перемещение итератора на узел дерева с максимальным ключом
Выход: True/False
Постусловия: Итератор установлен на узел дерева с максимальным ключом
Установка на следующий узел дерева:
Вход: Нет
Предусловия: size>0,конец дерева не достигнут
Процесс: Перемещение итератора на следующий узел дерева
Выход: True/False
Постусловия: Итератор установлен на следующий узел дерева/Или статус=Вне
Установка на предыдущий узел дерева:
Вход: Нет
Предусловия: size>0,указатель не в начале дерева
Процесс: Перемещение итератора на предыдущий узел дерева
Выход: True/False
Постусловия: Итератор установлен на предыдущий узел дерева/Или статус=Вне
Доступ к данным текущего узла на чтение/запись:
Вход: Нет
Предусловия: Итератор не выходит за пределы дерева
Процесс: Осуществление доступа к данным текущего узла на чтение/запись
Выход: Данные текущего узла/Ошибка
Постусловия: Нет
Определение шаблонного класса для коллекции «Двоичное дерево поиска»:
template class BST
BST(); //Конструктор
BST(BST *C); //Конструктор копирования
BST(); //Деструктор
void Balance(); //Определение критерия сбалансированности
bool Add(int,T &new_data); //Добавление элемента
bool Change(int,T &new_data); //Изменить значение
void RandTree(int,int,int); //Заполнить случайно
void SucessTree(int); //Заполнить упорядоченно
bool Delete(int); //Удаление
T& Get(int); //Чтение элемента по ключу
int GetBal(int); //Получение критерия сбалансированности
void Clear(); //Очистка дерева
int Search(T &val); //Поиск ключа по значению
void Show(); //Вывод дерева на экран
void L_t_R(); //L-t_R обход дерева
int SumCount(){return sum_oper;}; //Опрос количества операций
int Size(){return size;}; //Опрос размера списка
class iterator
iterator(BST *BT); //Конструктор итератора
bool Next(); //Установка на следующий узел
bool Prev(); //Установка на предыдущий узел
bool Begin(); //Установка на начало
bool End(); //Установка на конец
int Key(); //Считать текущий ключ
T& operator *(); //Доступ к значению текущего узла
bool Status(){return status;} //Получить статус итератора
};
};
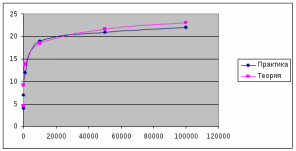
Таблицы и графики с полученными оценками трудоемкости операций.
Экспериментальная оценка средней трудоемкости операций дерева для среднего случая.
Размер
|
10
|
100
|
1000
|
10000
|
50000
|
100000
|
Поиск
|
3
|
6
|
11
|
18
|
20
|
20
|
Удаление
|
5
|
9
|
13
|
20
|
22
|
22
|
Вставка
|
4
|
7
|
12
|
19
|
20
|
21
|
Теоретически(1.39log2n)
|
5
|
9
|
14
|
18
|
22
|
23
|
Экспериментальная оценка средней трудоемкости дерева для худшего случая.
Размер
|
10
|
100
|
1000
|
10000
|
50000
|
100000
|
Поиск
|
6
|
55
|
466
|
4656
|
24867
|
55390
|
Удаление
|
6
|
51
|
533
|
5326
|
25548
|
52683
|
Вставка
|
6
|
49
|
458
|
4583
|
24345
|
48931
|
Теоретически(O(n/2))
|
5
|
50
|
500
|
5000
|
25000
|
50000
|
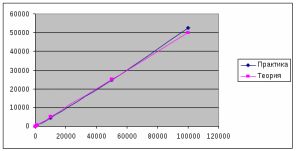
Вывод: Из приведенных таблиц и графиков видно, что теоретическая трудоемкость для среднего и худшего случаев практически совпадает с полученной.
Текст программы:
#include
#include
#include
#include
#include
template class stack //Стек
{
struct data
{
D el; //Данные стека
data *next; //Указатель на следующий элемент
};
bool empty; //Статус
data *top; //Указатель на верхний элемент
public:
stack(){top=NULL;empty=true;} //Конструктор
void Push(D &Elem) //Положить элемент
{
data *New=new data;
New->el=Elem;
if(empty){New->next=NULL;empty=false;}
else{New->next=top;}
top=New;
}
D& Pop() //Достать элемент
{
data *Del=top;
D Elem=Del->el;
if(Del->next==NULL){top=NULL;empty=true;}
else {top=Del->next;}
delete Del;
return Elem;
}
D& Read(){return top->el;} //Считать элемент
bool Empty(){return empty;} //Получить статус
};
template class BST
{
struct node
{
T data; //Значение
int key; //Ключ
node *left; //Указатель на левого сына
node *right; //Указатель на правого сына
int bal; //Критерий сбалансированности
};
int size; //Размер дерева
int sum_oper; //Число операций
bool Add1(node *N,node *P,int,T &new_data);
bool Change1(node *V,int,T &new_data);
bool Delete1(node *V,node *P,int);
bool Delete2(node *V,node *P);
void Clear1(node *C);
T& Get1(node *R,int);
int GetBal1(node *R,int);
bool Exist(node *R,int);
int Search1(node *F,T &val);
void Show1(node *R,int);
void L_t_R(node *R);
void Copy(node *C);
public:
node *root; //Указатель на головной элемент
BST(); //Конструктор
BST(BST *C); //Конструктор копирования
BST(); //Деструктор
void Balance(); //Определение критерия сбалансированности
bool Add(int,T &new_data); //Добавление элемента
bool Change(int,T &new_data); //Изменить значение
void RandTree(int,int,int); //Заполнить случайно
void SucessTree(int); //Заполнить упорядоченно
bool Delete(int); //Удаление
T& Get(int); //Чтение элемента по ключу
int GetBal(int); //Получение критерия сбалансированности
void Clear(); //Очистка дерева
int Search(T &val); //Поиск ключа по значению
void Show(); //Вывод дерева на экран
void L_t_R(); //L-t-R обход дерева
int SumCount(){return sum_oper;}; //Опрос количества операций
int Size(){return size;}; //Опрос размера списка
class iterator
{
BST *B;
node *itcur;
bool status;
bool Next(node *V,int K)
{
bool res;
res=false;
if(V==NULL)return false;
if(V->key>K){itcur=V;res=true;Next(V->left,K);}
else res=Next(V->right,K);
return res;
}
bool Prev(node *V,int K)
{
bool res;
res=false;
if(V==NULL)return false;
if(V->keyright,K);}
else res=Prev(V->left,K);
return res;
}
public:
iterator(BST *BT)
{
B=BT;
itcur=NULL;
status=false;
}
bool Next()
{
bool res;
if(status==false)return false;
res=Next(B->root,itcur->key);
if(res==false){itcur=NULL;status=false;}
return res;
}
bool Prev()
{
bool res;
if(status==false)return false;
res=Prev(B->root,itcur->key);
if(res==false){itcur=NULL;status=false;}
return res;
}
bool Begin()
{
if(B->root==NULL)return false;
for(itcur=B->root;itcur->left!=NULL;itcur=itcur->left);
status=true;
return true;
}
bool End()
{
if(B->root==NULL)return false;
for(itcur=B->root;itcur->right!=NULL;itcur=itcur->right);
status=true;
return true;
}
int Key()
{
if(status)return itcur->key;
else return -1;
}
T& operator *()
{
if(status)return itcur->data;
else throw -1;
}
bool Status(){return status;}
};
};
BST l;
BST::iterator it(&l);
//-------------------------------------------------------------------------------------------------
template
bool BST::Add1(node *N,node *P,int K,T &new_data)
{
if ((N==NULL)&&(P==NULL))
{N=new node;N->key=K;N->data=new_data;root=N;N->left=N->right=NULL;size++;return true;}
if (N==NULL)
{
N=new node;
N->key=K;
N->data=new_data;
if (K
key) {P->left=N;}
if (K>P->key) {P->right=N;}
N->left=N->right=NULL;
size++;
return true;
}
if (K==N->key) return false;
if (Kkey) {sum_oper++; return Add1(N->left,N,K,new_data);}
sum_oper++; return Add1(N->right,N,K,new_data);
}
//-------------------------------------------------------------------------------------------------
template
bool BST::Change1(node *V,int K,T &new_data)
{
if (V==NULL) return false;
if (V->key==K){V->data=new_data; return true;}
if (Kkey) return Change1(V->left,K,new_data);
return Change1(V->right,K,new_data);
}
//-------------------------------------------------------------------------------------------------
template
bool BST::Delete1(node *V,node *P,int K)
{
sum_oper++;
if (V==NULL) return false;
if (V->key==K) return Delete2(V,P);
if (Kkey) {return Delete1(V->left,V,K);}
return Delete1(V->right,V,K);
}
//-------------------------------------------------------------------------------------------------
template
bool BST::Delete2(node *V,node *P)
{
if (P!=NULL)
{
if ((V->left==NULL)&&(V->right==NULL))
{
if(P->key>V->key)P->left=NULL;
if(P->keykey)P->right=NULL;
delete V; size--;
return true;
}
if (V->left==NULL)
{
if (P->key>V->key){P->left=V->right; delete V; size--;return true;}
P->right=V->right; delete V; size--; return true;
}
if (V->right==NULL)
{
if (P->key>V->key){P->left=V->left; delete V;size--; return true;}
P->right=V->left; delete V; size--; return true;
}
}
if ((V->left==NULL)&&(V->right==NULL)){delete V;size--;root=NULL;return true;}
if (V->left==NULL) {root=V->right; delete V; size--; return true;}
if (V->right==NULL){root=V->left; delete V; size--; return true;}
if (V->left->right!=NULL)
{
V->key=V->left->right->key;
V->data=V->left->right->data;
return Delete2(V->left->right,V->left);
}
P=V->left;
V->key=P->key;
V->data=P->data;
V->left=P->left;
size--;
delete P;
return true;
}
//-------------------------------------------------------------------------------------------------
template
void BST::Clear1(node *C)
{
node* cur;
if(C!=NULL)
{
if (C->left!=NULL) Clear1(C->left);
cur=C->right;
delete C;
if (cur!=NULL) Clear1(cur);
}
}
//-------------------------------------------------------------------------------------------------
template
bool BST::Exist(node *R,int num)
{
if (R==NULL) return false;
if (num==R->key) return true;
if (num>R->key) return Exist(R->right,num);
return Exist(R->left,num);
}
//-------------------------------------------------------------------------------------------------
template
T& BST::Get1(node *R,int num)
{
try
{
sum_oper++;
if (R==NULL) throw -1;
if (R->key==num) return R->data;
if (numkey) return Get1(R->left,num);
return Get1(R->right,num);
}
catch(int){throw -1;}
}
//-------------------------------------------------------------------------------------------------
template
int BST::GetBal1(node *R,int num)
{
if (R->key==num) return R->bal;
if (numkey) return GetBal1(R->left,num);
return GetBal1(R->right,num);
}
//-------------------------------------------------------------------------------------------------
template
int BST::Search1(node *F,T &val)
{
int i,j;
i=-1;
if (F->left!=NULL) {i=Search1(F->left,val);}
if (F->right!=NULL){j=Search1(F->right,val);}
if (F->data==val) i=F->key;
if (i>j) return i;
return j;
}
//-------------------------------------------------------------------------------------------------
template
void BST::Show1(node *R,int level)
{
int i;
if (R==NULL)
{
for (i=0;i
cout<<" * \n";
}
else
{
Show1(R->right,level+1);
for (i=0;i
if (R->key<10) cout<<' '<key<<" \n";
else if (R->key<100) cout<key<<" \n";
else cout<key<<'\n';
Show1(R->left,level+1);
}
}
//-------------------------------------------------------------------------------------------------
template
void BST::L_t_R(node *R)
{
if(R!=NULL)
{
L_t_R(R->left);
cout<key<<' ';
L_t_R(R->right);
}
}
//-------------------------------------------------------------------------------------------------
template
void BST::Balance()
{
stack st1;
stack st2,st3;
node *R=root;
int l,r;
st1.Push(R);
while(st1.Empty()==false)
{
R=st1.Read();
if((st3.Empty())||(R->key!=st3.Read()))
while((R->right!=NULL)||(R->left!=NULL))
{
st3.Push(R->key);
if(R->left!=NULL) st1.Push(R->left);
if(R->right!=NULL) st1.Push(R->right);
R=st1.Read();
}
R=st1.Pop();
if (R->left==NULL)l=0;
else l=st2.Pop();
if (R->right==NULL)r=0;
else r=st2.Pop();
R->bal=r-l;
l++;r++;
if(st1.Empty()==false)
if (l>r) st2.Push(l);
else st2.Push(r);
if(st3.Empty()==false)
if(R->key==st3.Read())R->key=st3.Pop();
}
}
//-------------------------------------------------------------------------------------------------
template
void BST::Copy(node *C)
{
if(C!=NULL)
{
add(C->key,C->data);
Copy(C->left);
Copy(C->right);
}
}
//-------------------------------------------------------------------------------------------------
template
BST::BST()
{
root=NULL;
size=0;
sum_oper=0;
}
//-------------------------------------------------------------------------------------------------
template
BST::BST(BST *C)
{
size=0;
sum_oper=0;
Copy(C->root);
}
//-------------------------------------------------------------------------------------------------
template
BST::
BST()
{
Clear();
}
//-------------------------------------------------------------------------------------------------
template
bool BST::Add(int K,T &new_data)
{
sum_oper=0;
bool res;
res=Add1(root,NULL,K,new_data);
return res;
}
//-------------------------------------------------------------------------------------------------
template
bool BST::Change(int K,T &new_data)
{
return Change1(root,K,new_data);
}
//-------------------------------------------------------------------------------------------------
template
void BST::RandTree(int rand_BST_size, int rand_BST_interval, int rand_key_interval)
{
srand((unsigned)time( NULL ));
for(int i=0;i
{
int r=rand()*rand()%rand_BST_interval;
int k=rand()*rand()%rand_key_interval+1;
Add(k,r);
}
}
//-------------------------------------------------------------------------------------------------
template
void BST::SucessTree(int BST_size)
{
for(int i=0;i
}
//-------------------------------------------------------------------------------------------------
template
bool BST::Delete(int num)
{
sum_oper=0;
bool res;
res=Delete1(root,NULL,num);
return res;
}
//-------------------------------------------------------------------------------------------------
template
void BST::Clear()
{
Clear1(root);
size=0,sum_oper=0;
root=NULL;
}
//-------------------------------------------------------------------------------------------------
template
T& BST::Get(int num)
{
sum_oper=0;
try {return Get1(root,num);}
catch(int){throw -1;}
}
//-------------------------------------------------------------------------------------------------
template
int BST::GetBal(int num)
{
if (Exist(root,num)) return GetBal1(root,num);
throw -1;
}
//-------------------------------------------------------------------------------------------------
template
int BST::Search(T &val)
{
if(root==NULL)return -2;
return Search1(root,val);
}
//-------------------------------------------------------------------------------------------------
template
void BST::Show()
{
Show1(root,0);
}
//-------------------------------------------------------------------------------------------------
template
void BST::L_t_R()
{
L_t_R(root);
cout<<'\n';
}
//-------------------------------------------------------------------------------------------------
void selMenu()
{
do
{
switch(Menu())
{
case 1:
{
int data,key;
system("cls");
cout<<"Введите ключ:\n ";
cin>>key;
cout<<"\nВведите значение: \n";
cin>>data;
if(l.Add(key,data));
else cout<<"\nОшибка! Узел с таким ключом уже существует!";
break;
}
case 2:
{
int rand_BST_size;
system("cls");
cout<<"Введите размер дерева: \n";
cin>>rand_BST_size;
system("cls");
l.RandTree(rand_BST_size,100,99);
break;
}
case 3:
{
int key,data;
system("cls");
cout<<"Введите ключ: \n";
cin>>key;
cout<<"\nВведите значение: \n";
cin>>data;
if(l.Change(key,data));
else cout<<"\nОшибка! Узла с заданным ключом не существует!";
break;
}
case 4:
{
system("cls");
int key;
cout<<"Введите ключ: \n";
cin>>key;
if(l.Delete(key));
else cout<<"\nОшибка! Узла с заданным ключом не существует!";
break;
}
case 5:
{
system("cls");
int key;
cout<<"Введите ключ: \n";
cin>>key;
try
{
cout<<"\nЗначение: "<
}
catch(int)
{
cout<<"\nОшибка! Узла с заданным ключом не существует!";
}
break;
}
case 6:
{
system("cls");
int val,key;
cout<<"Введите искомое значение: \n";
cin>>val;
key=l.Search(val);
if(key == -1) cout<<"\nНе найдено!";
if(key == -2) cout<<"Ошибка!";
else cout<
break;
}
case 7:
{
system("cls");
if(l.Size() == 0)cout<<"Дерево пустое";
else
cout<<"В дереве: "<
break;
}
case 8:
{
system("cls");
l.Show();
break;
}
case 9:
{
l.Clear();
break;
}
case 10:
{
int num = 0;
system("cls");
l.Show();
l.L_t_R();
break;
}
case 11:
{
system("cls");
int key;
cout<<"Введите ключ: ";
cin>>key;
try
{
cout<<"\nКритерий сбалансированности узла: "<
}
catch(int)
{
cout<<"\nОшибка! Узла с заданным ключом не существует!";
}
break;
}
case 12:
{
l.Clear();
int *a=NULL,i,s,sser=0,sdel=0,sins=0;
int tsize=0,toper=0,ran;
system("cls");
cout<<"Введите размер дерева: ";
cin>>tsize;
a=new int [tsize];
toper=tsize/10;
for(i=0;i
s=tsize;
while(l.Size()
{ran=rand()*rand()%s;s--;l.Add(a[ran],a[ran]);a[ran]=a[s];}
delete a;
for(i=1;i<=toper;i++)
{
if((i%10)==0)
{
ran=2*(rand()*rand()%tsize)+1;
try{l.Get(ran);}catch(int){};
sser+=l.SumCount();
ran=2*(rand()*rand()%tsize)+1;
l.Delete(ran);
sdel+=l.SumCount();
ran=2*(rand()*rand()%tsize);
l.Add(ran,ran);
sins+=l.SumCount();
}
else
{
ran=2*(rand()*rand()%tsize);
try{l.Get(ran);}catch(int){};
sser+=l.SumCount();
ran=2*(rand()*rand()%tsize)+1;
l.Add(ran,ran);
sins+=l.SumCount();
l.Delete(ran);
sdel+=l.SumCount();
}
}
cout<<"\nПоиск: "<<(double)sser/toper<
cout<<"Удаление: "<<(double)sdel/toper<
cout<<"Вставка: "<<(double)sins/toper<
cout<<"size "<
getch();
break;
}
case 13:
{
l.Clear();
int i,sser=0,sdel=0,sins=0;
int tsize=0,toper=0,ran;
system("cls");
cout<<"Введите размер дерева: ";
cin>>tsize;
toper=10;
for(i=0;i
{ran=2*i;l.Add(ran,ran);}
for(i=1;i<=toper;i++)
{
if((i%10)==0)
{
ran=2*(rand()*rand()%tsize)+1;
try{l.Get(ran);}catch(int){};
sser+=l.SumCount();
ran=2*(rand()*rand()%tsize)+1;
l.Delete(ran);
sdel+=l.SumCount();
ran=2*(rand()*rand()%tsize);
l.Add(ran,ran);
sins+=l.SumCount();
}
else
{
ran=2*(rand()*rand()%tsize);
try{l.Get(ran);}catch(int){};
sser+=l.SumCount();
ran=2*(rand()*rand()%tsize)+1;
l.Add(ran,ran);
sins+=l.SumCount();
l.Delete(ran);
sdel+=l.SumCount();
}
}
cout<<"\nПоиск: "<<(double)sser/toper<
cout<<"Удаление: "<<(double)sdel/toper<
cout<<"Вставка: "<<(double)sins/toper<
cout<<"size "<
getch();
break;
}
case 14:
{
if(it.Status()) cout<<"Внутри дерева.";
else cout<<"Вне дерева.";
break;
}
case 15:
{
if(it.Begin()) cout<
else cout<<"Ошибка!";
break;
}
case 16:
{
if(it.Next()) cout<
else cout<<"Ошибка!";
break;
}
case 17:
{
if(it.Prev()) cout<
else cout<<"Ошибка!";
break;
}
case 18:
{
if(it.End()) cout<
else cout<<"Ошибка!";
break;
}
case 19:
{
try
{
cout<<"Значение: "<<*it;
}
catch(int)
{
cout<<"Ошибка!";
}
break;
}
case 20:
{
try
{
cout<<"Введите значение\n";
cin>>*it;
}
catch(int)
{
cout<<"Ошибка!";
}
break;
}
case 21:
{
l.Balance();
break;
}
default: return;
}
}
while (1);
}
//-------------------------------------------------------------------------------------------------
void main()
{
system("cls");
selMenu();
}
|
 Скачать 64.63 Kb.
Скачать 64.63 Kb.

