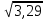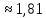Теория вероятностей и математическая статистика. Контрольная работа Канев ВС. Задание Комбинаторика Сколько 5ти буквенных слов можно составить из букв слова ходок решение
 Скачать 1.82 Mb. Скачать 1.82 Mb.
|
|
Задание 1. Комбинаторика Сколько 5-ти буквенных слов можно составить из букв слова Х О Д О К Решение. Переставить буквы в слове можно 5! способами. При этом в слове имеется две одинаковые буквы – О. Если менять местами эти буквы в конкретной расстановке, то слова будут получаться одинаковые. Следовательно, общее число слов, составленных перестановкой букв из слова Х О Д О К будет равно 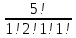 = = 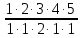 = 60 = 60Ответ: 60 слов. Задание 2. Основные теоремы Две трети всех сообщений передается по первому каналу связи, остальные - по второму. Вероятность искажения при передаче по первому каналу равна 0,01, по второму - 0,04. Какова вероятность искажения произвольно взятого сообщения? Решение. Рассмотрим следующие два события: Событие A – произвольно взятое сообщение искажено; событие B – произвольно взятое сообщение не искажено. Выдвинем следующие гипотезы: Н1 – сообщение передавалось по первому каналу связи; Н2 – сообщение передавалось по второму каналу связи. Вероятности гипотез, согласно статистическому определению вероятности, равны P (Н1) = 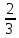 , P (Н2) = , P (Н2) = 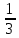 . .Условные вероятности события А известны: P(А/Н1) = 0,01, P(А/Н2) = 0,04. И по формуле полной вероятности P(А) = P ( Н1 )*P(А/Н1) + P ( Н2 )*P(А/Н2) = 0,02 Ответ: 0,02. Задание 3. Случайные величины Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины, заданной рядом распределения Решение. Запишем формулу для вычисления математического ожидания и подставим в неё данные задачи:
Запишем формулу для вычисления дисперсии и подставим в неё данные задачи:
Среднее квадратическое отклонение вычисляется по формуле
Ответ: Задание 4. Нормальное распределение случайной величины Случайная величина распределена по нормальному закону с параметрами a = 7, 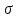 = 2. Найдите вероятность того, что случайная величина принимает значения из интервала [5; 10]. = 2. Найдите вероятность того, что случайная величина принимает значения из интервала [5; 10].Решение. Вероятность попадания нормально распределённой величины в интервал вычисляется по формуле где Фo (x) - функция Лапласа, её значения можно найти в таблице в конце любого учебника по теории вероятностей. Согласно условиям задачи, имеем в таблице находим значение Фo(1,5) = 0,4331928; в таблице находим ближайшее значение Фo (1) = 0,3413447; с учётом того, что функция Лапласа нечётная, получаем Фo (-1) = −0,3413447; подставим в формулу:
Ответ: 0,7745375. |