Курсовая-неск перем. Задание Найти области определения функций Задание Вычислить дифференциалы 2го порядка от функций
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
Вариант №25 Задание 1. Найти области определения функций 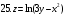 Задание 2. Вычислить дифференциалы 2-го порядка от функций. 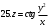 Задание 3. Найти указанные производные от сложных функций. 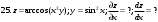 Задание 4.Найти производные функций, заданных неявно. 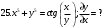 Задание 5.Даны функция 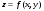 и две точки и две точки 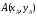 и и 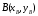 . .Вычислить значение 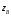 функции в точке B. функции в точке B.Вычислить значение 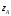 функции в точке А и найти приближенное значение функции в точке А и найти приближенное значение 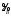 исходя из значения исходя из значения 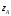 , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: Составить уравнения касательной плоскости и нормали к поверхности 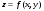 в точке в точке  . .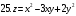  Задание 6. Исследовать на экстремум функции. 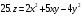 Задание 7. Даны функция 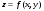 и две точки и две точки  и и 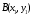 . .Найти: 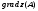 ; ;производную функцию в точке А по направлению к точке В. 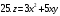 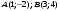 Вариант №26 Задание 1. Найти области определения функций 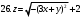 Задание 2. Вычислить дифференциалы 2-го порядка от функций. 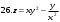 Задание 3. Найти указанные производные от сложных функций. 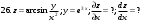 Задание 4.Найти производные функций, заданных неявно. 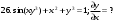 Задание 5.Даны функция 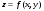 и две точки и две точки 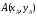 и и 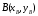 . .Вычислить значение 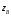 функции в точке B. функции в точке B.Вычислить значение 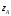 функции в точке А и найти приближенное значение функции в точке А и найти приближенное значение 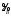 исходя из значения исходя из значения 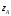 , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: Составить уравнения касательной плоскости и нормали к поверхности 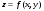 в точке в точке  . .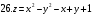 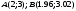 Задание 6. Исследовать на экстремум функции. 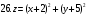 Задание 7. Даны функция 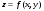 и две точки и две точки  и и 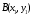 . .Найти: 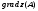 ; ;производную функцию в точке А по направлению к точке В. 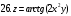 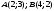 Вариант №27 Задание 1. Найти области определения функций 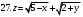 Задание 2. Вычислить дифференциалы 2-го порядка от функций. 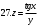 Задание 3. Найти указанные производные от сложных функций. 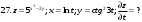 Задание 4.Найти производные функций, заданных неявно. 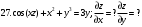 Задание 5.Даны функция 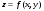 и две точки и две точки 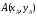 и и 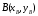 . .Вычислить значение 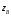 функции в точке B. функции в точке B.Вычислить значение 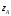 функции в точке А и найти приближенное значение функции в точке А и найти приближенное значение 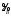 исходя из значения исходя из значения 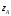 , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: Составить уравнения касательной плоскости и нормали к поверхности 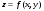 в точке в точке  . .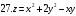 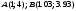 Задание 6. Исследовать на экстремум функции. 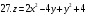 Задание 7. Даны функция 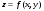 и две точки и две точки  и и 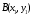 . .Найти: 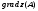 ; ;производную функцию в точке А по направлению к точке В. 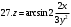 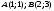 Вариант №28 Задание 1. Найти области определения функций 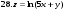 Задание 2. Вычислить дифференциалы 2-го порядка от функций. 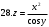 Задание 3. Найти указанные производные от сложных функций. 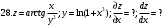 Задание 4.Найти производные функций, заданных неявно. 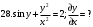 Задание 5.Даны функция 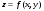 и две точки и две точки 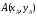 и и 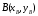 . .Вычислить значение 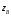 функции в точке B. функции в точке B.Вычислить значение 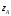 функции в точке А и найти приближенное значение функции в точке А и найти приближенное значение 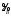 исходя из значения исходя из значения 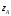 , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: Составить уравнения касательной плоскости и нормали к поверхности 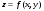 в точке в точке  . .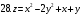 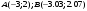 Задание 6. Исследовать на экстремум функции. 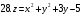 Задание 7. Даны функция 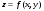 и две точки и две точки  и и 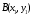 . .Найти: 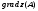 ; ;производную функцию в точке А по направлению к точке В. 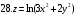 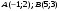 Вариант №29 Задание 1. Найти области определения функций 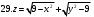 Задание 2. Вычислить дифференциалы 2-го порядка от функций. 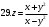 Задание 3. Найти указанные производные от сложных функций. 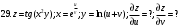 Задание 4.Найти производные функций, заданных неявно. 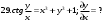 Задание 5.Даны функция 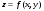 и две точки и две точки 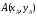 и и 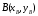 . .Вычислить значение 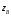 функции в точке B. функции в точке B.Вычислить значение 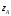 функции в точке А и найти приближенное значение функции в точке А и найти приближенное значение 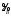 исходя из значения исходя из значения 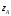 , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: Составить уравнения касательной плоскости и нормали к поверхности 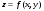 в точке в точке  . .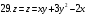 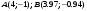 Задание 6. Исследовать на экстремум функции. 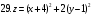 Задание 7. Даны функция 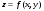 и две точки и две точки  и и 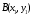 . .Найти: 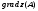 ; ;производную функцию в точке А по направлению к точке В. 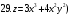 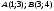 Вариант №30 Задание 1. Найти области определения функций 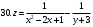 Задание 2. Вычислить дифференциалы 2-го порядка от функций. 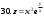 Задание 3. Найти указанные производные от сложных функций. 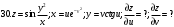 Задание 4.Найти производные функций, заданных неявно. 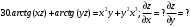 Задание 5.Даны функция 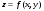 и две точки и две точки 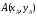 и и 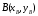 . .Вычислить значение 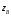 функции в точке B. функции в точке B.Вычислить значение 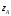 функции в точке А и найти приближенное значение функции в точке А и найти приближенное значение  исходя из значения исходя из значения  , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: , заменив приращение функции дифференциалом, и оценить относительную погрешность, возникающую при такой замене: Составить уравнения касательной плоскости и нормали к поверхности  в точке в точке  . .  Задание 6. Исследовать на экстремум функции.  Задание 7. Даны функция  и две точки и две точки  и и  . .Найти:  ; ;производную функцию в точке А по направлению к точке В.   |
