Контрольная работа по математике ТУСУР. Контольная работа 2.1. Задание Найти предел последовательности Решение
 Скачать 47.25 Kb. Скачать 47.25 Kb.
|
|
Задание 1. Найти предел последовательности: Решение: Исходная последовательность является рациональной дробью, поэтому ее предел определяется как отношение коэффициентов при старших степенях 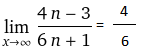 Задание 2. Найти предел последовательности: Решение: Непосредственное применение предела к исходной последовательности дает неопределенность типа 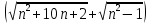 , тогда в числителе получим разность квадратов и проведем преобразования: , тогда в числителе получим разность квадратов и проведем преобразования: 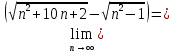 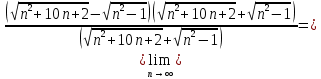 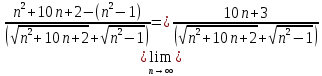 Теперь под знаком предела находится рациональная дробь, ее предел равен коэффициентам при старшей степени 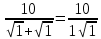 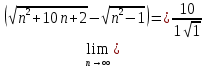 Задание 3. Найти предел последовательности:  . .Решение: Приведем исходную последовательность к виду:  , предел которой, как мы знаем, при любом , предел которой, как мы знаем, при любом 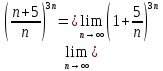 Сделаем замену 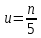 , тогда: , тогда: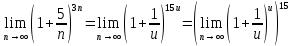 Под знаком внешней степени находится предел числа  = =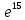 Задание 4. Написать в простейшей форме общий член ряда: Решение: Распишем заданные члены ряда, выделяя в их выражениях номер члена: 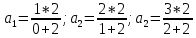 , откуда общий член: , откуда общий член: 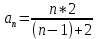 . .Задание 5. Исследовать сходимость ряда с помощью признака сравнения: Решение: Сравним исходный ряд с геометрическим рядом при 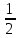 , то есть с рядом , то есть с рядом 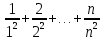 , откуда имеем , откуда имеем 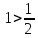 , ,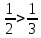 . .Так как геометрический ряд сходится, и каждый член исходного ряда меньше его членов, то на основании признака сравнения делаем вывод, что исходный ряд сходится. Ответ: исходный ряд сходится. Задание 6. Исследовать сходимость ряда с помощью признака Даламбера:  . .Решение: 1)Найдем предел отношения 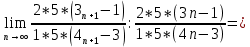 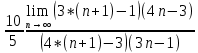 = =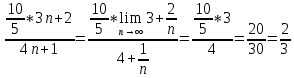 Поскольку α меньше 1, то ряд расходится. Задание 7. Вычислить какое число членов ряда надо взять, чтобы получить его сумму с точностью до 0,01:  . .Решение: Покажем сходимость данного ряда, применяя признак Лейбница: 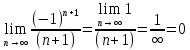 . Для этого вычислим несколько первых членов ряда и покажем, что они убывают по абсолютной величине: . Для этого вычислим несколько первых членов ряда и покажем, что они убывают по абсолютной величине: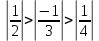 >... Так как знаменатель увеличивает свое значение, величина дроби уменьшается. Отсюда, согласно признаку Лейбница, исходный ряд является сходящимся. >... Так как знаменатель увеличивает свое значение, величина дроби уменьшается. Отсюда, согласно признаку Лейбница, исходный ряд является сходящимся.По следствию теоремы Лейбница имеем 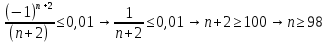 Задание 8. Исследовать сходимость ряда и, если он сходится, установить абсолютно или условно:  . .Решение: Установим сходимость ряда по признаку Лейбница: 1)вычислим предел общего члена: 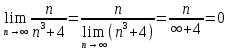 2) запишем несколько членов последовательности и убедимся, что они убывают по абсолютной величине: 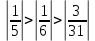 , значит, по признаку Лейбница, ряд сходится. , значит, по признаку Лейбница, ряд сходится.Ряд будет абсолютно сходящимся, если сходится ряд, составленный из его абсолютных величин: 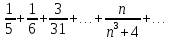 . .По признаку Даламбера: 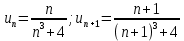 , то , то 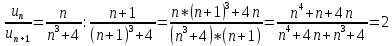 Поскольку α больше 1, то ряд сходится. При сравнении с геометрическим рядом при a=2 и q=1/2 следует вывод об абсолютной сходимости рассматриваемого ряда, т.к.: 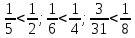 , то есть , то есть 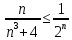 . . |
