Лузина-эконометрика. Задание Теоретические основы эконометрики
 Скачать 0.56 Mb.
|
|
Задание: 1. Запишите уравнение многофакторной регрессии и определите для нее минимальный объем выборки. Дайте экономическую интерпретацию полученной модели. Если известно, что  ,  ,  ,  ,  ,  ,  ,  ,  .2. Укажите, какие фиктивные переменные использованы в модели. 3. Проверьте факторы на мультиколлинеарность и устраните её. 4. Запишите новое уравнение многофакторной регрессии, после устранения мультиколлинеарности. Решение: Пусть α = 154. 1. Тогда уравнение многофакторной регрессии будет выглядеть следующим образом: = -22,09–21,75х1 + 1,24х2 + 0,19х3 + 0,1х4 + 0,79х5 +34,8х6 + 30,48х7 -0,4х8. Экономическая интерпретация полученной модели: Квартиры в районе А стоят на 21,75 % дешевле, чем в районе В. Наличие большего количества комнат увеличивает стоимость квартиры на 1,24 тыс. $. При увеличении общей площади на 1м2 стоимость квартиры возрастает на 0,19 тыс. $. При увеличении жилой площади на 1 м2 стоимость квартиры увеличивается на 0,1 тыс. $. При увеличении площади кухни на 1 м2 стоимость квартиры увеличивается на 0,79 тыс. $. Квартиры на средних этажах стоят на 34,8 % дороже, чем на крайних. Квартиры в кирпичных домах стоят на 30,48% дороже, чем в панельных. При увеличении срока сдачи дома на 1 мес. стоимость квартиры уменьшается на 0,4 тыс. $. Минимальный объем выборки определяем по формуле: N min = 5*(m + n). В нашем случаем m = 8 (т.к. в модель включены 8 факторов), n = 1 (т.к. в модели 1 свободный член – «а»). Следовательно, N min = 5*(8 + 1) = 45, т.е. для получения статистически значимой модели необходимо отобрать 45 квартир и собрать по ним необходимые данные. 2. В модели использована 1 фиктивная переменная – наименование района, т.к. в построении модели участвуют 2 района – «а» и «б», которым присвоены количественные значения «1» и «2» соответственно. Качественные признаки можно задавать с помощью фиктивных переменных. Обычно фиктивным переменным присваивают значение 1 и 2. Например: тип строения = 1, если этажи средние; 2, если этажи крайние. тип строения = 1, если кирпичное; 2, если панельное. Следовательно, фиктивные переменные были использованы в модели по таким параметрам как: этаж (средний или крайний), тип дома (панельный или кирпичный). 3. Проверим факторы на мультиколлинеарность. Мультиколлинеарная зависимость присутствует, если 
Это условие выполняется для следующих пар факторов х3 и х2, х4 и х2, х4 и х3, х5 и х4:  ,   ,  ,  .Найдены мультиколлинеарные факторы. Для устранения мультиколлинеарности используется метод исключения переменных. Будем исключать факторы, имеющие наименьшее значение  . Рассмотрим первую пару мультиколлинеарных факторов . Для исключения переменных необходимо знать, как каждый из факторных признаков связан с результативным признаком «Y». Эта зависимость отражается в последней строке матрицы парной корреляции. Итак  ,  . Далее необходимо сравнить эти значения:  > . Следовательно, факторный признак «х2» из модели можно исключить, т.к. его связь с результативным признаком меньше, чем у «х3». Аналогично, рассматриваются оставшиеся пары. Вторая пара . Следовательно, факторный признак «х2» из модели можно исключить, т.к. его связь с результативным признаком меньше, чем у «х4». Третья пара . Следовательно, факторный признак «х4» из модели можно исключить, т.к. его связь с результативным признаком меньше, чем у «х3». Четвертая пара . Следовательно, факторный признак «х5» из модели можно исключить, т.к. его связь с результативным признаком меньше, чем у «х4». 4. После устранения мультиколлинеарности уравнение многофакторной регрессии будет выглядеть следующим образом: = а+b1х1+b3х3 + b6x6+b7x7+b8x8. Минимальный объем выборки определим по формуле: N min = 5*(m + n). В нашем случаем m = 5 (т.к. в модель включены 5 факторов), n = 1 (т.к. в модели 1 свободный член – «а»). Следовательно, N min = 5*(5 + 1) = 30, т.е. для получения статистически значимой модели необходимо отобрать 30 квартир и собрать по ним необходимые данные. Задание 6. Модели временных рядов 6.1. Приведите примеры факторов, формирующих трендовую, сезонную и случайную компоненту. 6.2. Постройте модель сезонных колебаний дохода торгового предприятия, используя первую гармонику ряда Фурье по данным, приведенным в таблице 13. Изобразите графически. Таблица 13
Воспользуйтесь вспомогательной табл. 14. Таблица 14 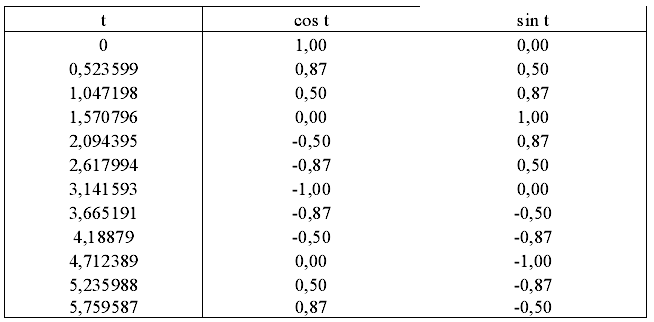 Решение: Пусть, например, число а =14. Тогда исходная таблица будет выглядеть следующим образом:
Если мы рассматриваем год как цикл, то n=12. Циклическая компонента S может быть разложена в ряд Фурье:  А первая гармоника ряда Фурье будет выглядеть следующим образом:  Где параметры уравнения могут быть найдены по формулам: 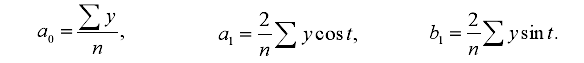 Получили а0 = 42,46 . Найдем промежуточные значения: 
Найдем коэффициенты: а1=(2/12) · -54,3885 = -9,06 b1=(2/12) · -22,0585=-3,68 Модель сезонных колебаний дохода торгового предприятия: yt=42,46 – 9,06 · cos t – 3,68 · sin t.
По фактическим и теоретическим значениям строим график ряда Фурье: 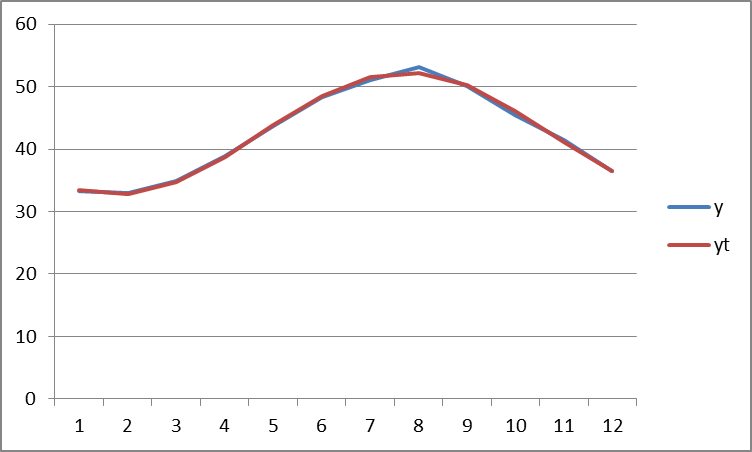 |