Лузина-эконометрика. Задание Теоретические основы эконометрики

• Название: Задание Теоретические основы эконометрики
• Дата: 18.04.2022
• Размер: 0.56 Mb.
• Имя файла: Лузина-эконометрика.doc
• Тип: Документы; #482600
• страница: 4 из 4

Задание 7. Модели с распределенным лагом
Для модели Y_t = -α + (α – 50)x_t + x_t-1 + (405 – α)x_t-2 определите краткосрочный, промежуточный и долгосрочный мультипликаторы, вклад каждого лага, средний лаг модели. Сделайте выводы.

Решение:

Если а=14, то модель:

Y_t = -14 +204х_t + 63,5х_t-1 + 151х_t-2

Краткосрочный мультипликатор – это коэффициент при x_t, он равен 204. Следовательно, увеличение факторного показателя на одну единицу своего измерения приведет к среднему росту результативного показателя на 204 единицы своего измерения в том же периоде.

В модели один промежуточный мультипликатор, его можно найти как 204 + 63,5 = 267,5. Следовательно, увеличение факторного показателя на одну единицу своего измерения приведет к среднему росту результативного показателя на 267,5 единиц своего измерения в момент времени t+1.

Долгосрочный мультипликатор равен 204 + 63,5 + 151 = 418,5. В долгосрочной перспективе увеличение факторного показателя на одну единицу своего измерения приведет к среднему росту результативного показателя на 418,5 единиц своего измерения.

Вклад каждого лага в модель равен:

W1 = 204/418,5 = 0,49;

W2 = 63,5/418,5 = 0,15;

W3 = 151/418,5 = 0,36.

Следовательно, 49% общего увеличения результативного показателя происходит в текущем моменте времени; 15% - в момент времени (t+1); 36% - в момент времени (t+2).

Проверим свойство

W₁ + W₂ + W₃ = 0,49+0,15+0,36 = 1

1. Средний лаг модели равен:



Небольшая величина лага (менее 1 мес.) подтверждает, что большая часть эффекта роста результативного признака проявляется в течение текущего периода времени.

Задание 8. Цепи Маркова
В торгово-розничную сеть поступило 3 вида взаимозаменяемой продукции разных производителей: А1, А2, А3. Предположим, что покупатели приобретают продукцию только одного из них. Пусть в среднем они стремятся поменять её не более одного раза в год, и вероятности таких изменений постоянны.

Результаты маркетинговых исследований покупательского спроса на продукцию дали следующее процентное соотношение:

Х1 % покупателей продукции А1 переходит на продукцию А2,

Х2 % покупателей продукции А2 – на продукцию А3,

Х3 % покупателей продукции А3 – на продукцию А1,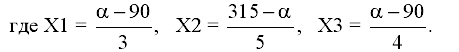



Требуется:

1. Построить граф состояний.

2. Составить матрицу переходных вероятностей для средних годовых изменений.

3. Предположить, что общее число покупателей постоянно, и определить, какая доля из их числа будет покупать продукцию А1, А2 и А3 через 2 года.

4. Определить какая продукция будет пользоваться наибольшим спросом.

Решение:

Если число а =14. Тогда

Х₁ = (154– 90):3 = 54,7;

Х₂ = (315 – 154):5 = 12,2;

Х₃ = (154 – 90):4 = 41.

Построим граф состояний: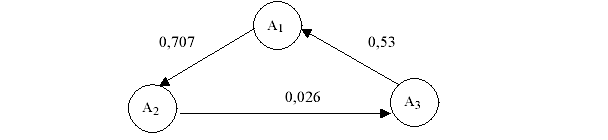


0,547

0,122

0,41

Составим матрицу переходных вероятностей:

1 -0,547	0,547	0		0,453	0,547	0
0	1-0,122	0,122		0	0,878	0,122
0,41	0	1-0,41		0,41	0	0,59

Зададим вектор начальных вероятностей: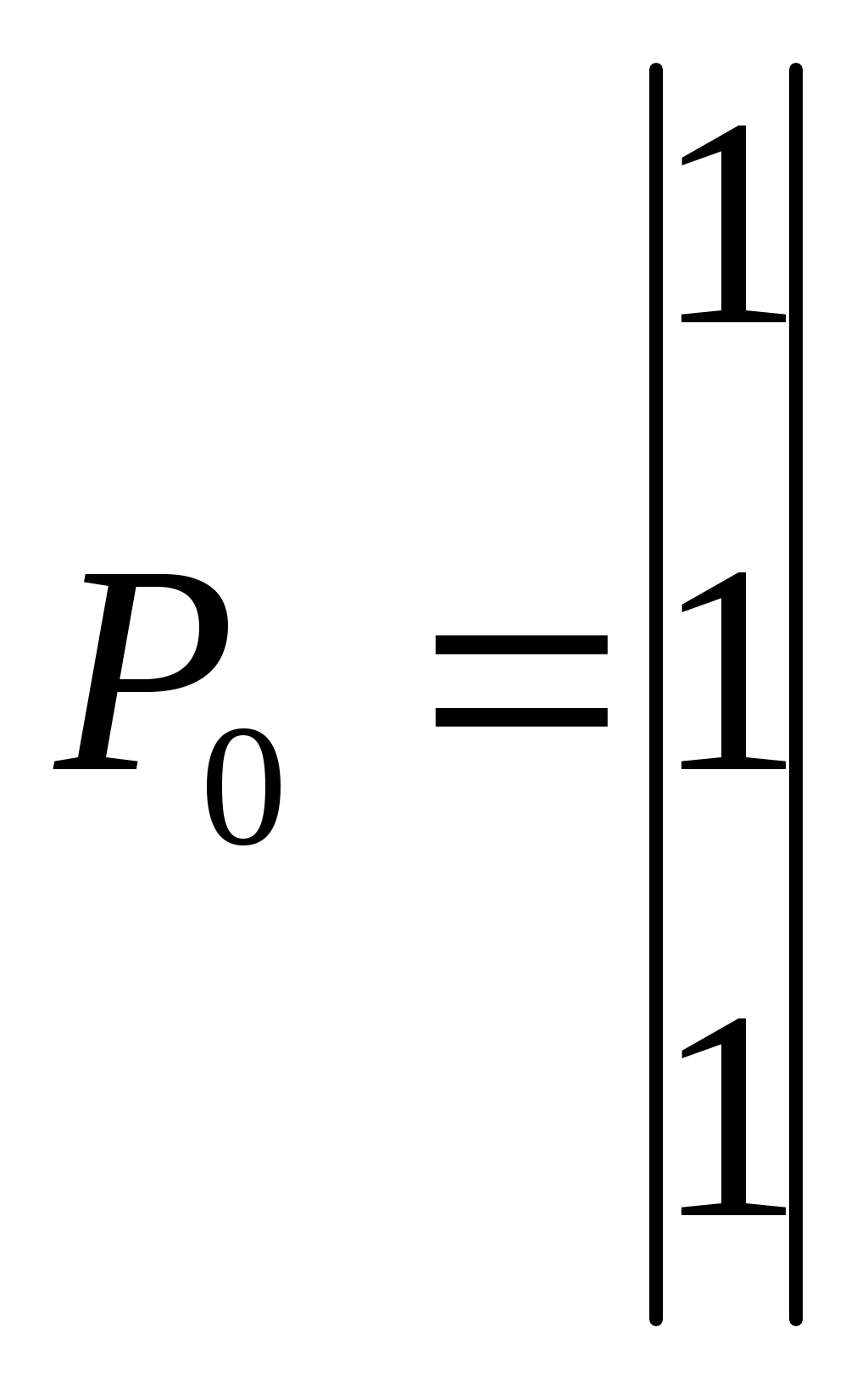



то есть Р₁(0)=1, Р₂(0)=1, Р₃(0)=1.

Определим вероятности состояний после первого шага (после первого года):

Р₁(1)= Р₁(0) · Р₁₁ + Р₂(0) · Р₂₁ + Р₃(0)· Р₃₁= 1 · 0,453 + 1 · 0 + 1 · 0,41 = 0,863

Р₂(1)= Р₁(0) · Р₁₂ + Р₂(0) · Р₂₂ + Р₃(0)· Р₃₂= 1 · 0,547 + 1 · 0,878 + 1 · 0 = 1,425

Р₃(1)= Р₁(0) · Р₁₃ + Р₂(0) · Р₂₃ + Р₃(0)· Р₃₃= 1 · 0 + 1 · 0,122 + 1 · 0,59 = 0,712

Определим вероятности состояний после второго шага (после второго года):

Р₁(2)= Р₁(1) · Р₁₁ + Р₂(1) · Р₂₁ + Р₃(1)· Р₃₁= 0,863·0,453 + 1,425·0 + 0,712·0,41 = 0,683

Р₁(2)= Р₁(1) · Р₁₂ + Р₂(1) · Р₂₂ + Р₃(1)· Р₃₂= 0,863·0,547 + 1,425·0,878 + 0,712·0 = 1,723

Р₁(2)= Р₁(1) · Р₁₃ + Р₂(1) · Р₂₃ + Р₃(1)· Р₃₃= 0,863·0 + 1,425·0,122 + 0,712·0,59 = 0,594
Вывод: через 2 года около 68% покупателей будут приобретать продукцию А1; число покупателей продукции А2 увеличится в 1,72 раза; 59,4% покупателей будут приобретать продукцию А2. Продукция А2 будет пользоваться наибольшим спросом.
Задача 9. Система эконометрических уравнений
Проверить идентифицированы ли уравнения систем эконометрических уравнений с помощью необходимого условия идентификации.

При значении α равных 202 – 300: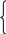



Решение:

– эндогенные переменные, соответственно величины спроса, предложения и цены. Для каждого из уравнений n = 3, Р=0, I=0. Следовательно, I+1n, Р+1
В этом случае изменяют модель так, чтобы она, с одной стороны, содержала основные эндогенные и экзогенные переменные, которые определяют спрос и предложение, а с другой – была эконометрически разрешима.
Список используемой литературы
1. Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 2012.

2. Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем. – М.: Финансы и статистика, 2011. – 368 с.

3. Елисеева И. И. и др. Практикум по эконометрике. – М.: Финансы и статистика, 2011. – 192 с.

4. Маленво Э. Статистические методы эконометрики. – М.: Статистика, 2012. – Т. 1; 1976. – Т. 2.