Главная страница
Навигация по странице:

  • Перечень вопросов, выносимых на экзамен по учебной дисциплине «Математика» для студентов 2 курса специальности 23.02.03

  • Задание 1. Проверяемые результаты обучения: З.1

  • Задание 2. Проверяемые результаты обучения: З.1

  • Задание 3 Проверяемые результаты обучения: З.1

  • Задание 4. Проверяемые результаты обучения: З.1

  • Задание 5. Проверяемые результаты обучения: У.1

  • Задание 6. Проверяемые результаты обучения: З.1

    		•

    Задания для промежуточной аттестации. Задания для проведения промежуточной аттестации ТО. Задания для проведения промежуточной аттестации Перечень вопросов, выносимых на экзамен по учебной дисциплине Математика


    Скачать 75.43 Kb.
    НазваниеЗадания для проведения промежуточной аттестации Перечень вопросов, выносимых на экзамен по учебной дисциплине Математика
    АнкорЗадания для промежуточной аттестации
    Дата26.02.2022
    Размер75.43 Kb.
    Формат файлаdocx
    Имя файлаЗадания для проведения промежуточной аттестации ТО.docx
    ТипИсследование
    #374593

    Задания для проведения промежуточной аттестации

    Перечень

    вопросов, выносимых на экзамен

    по учебной дисциплине «Математика»

    для студентов 2 курса специальности 23.02.03

    «Техническое обслуживание и ремонт автомобильного транспорта»

    1. Понятие предела функции. Методы вычисления пределов многочлена и частного двух многочленов.

    2. Асимптоты графика функции.

    3. Понятие производной функции. Производные элементарных функций.

    4. Понятие производной функции. Основные правила дифференцирования.

    5. Дифференцирование тригонометрических и обратных тригонометрических функций.

    6. Вторая производная. Производные высших порядков

    7. Сложная функция. Правило дифференцирования сложных функций.

    8. Исследование функции с помощью производной. Общая схема исследования функции.

    9. Понятие выпуклости и точек перегиба функции. Достаточное условие выпуклости функции.

    10. Исследование функции с помощью производной. Точки экстремума. Промежутки возрастания и убывания функции.

    11. Нахождение наибольшего и наименьшего значения функции на отрезке.

    12. Понятие первообразной функции. Первообразные основных элементарных функций.

    13. Неопределенный интеграл. Метод непосредственного интегрирования.

    14. Неопределенный интеграл. Метод замены переменной.

    15. Определенный интеграл. Формула Ньютона-Лейбница.

    16. Вычисление площади криволинейной трапеции с помощью определенного интеграла.

    17. Понятие о дифференциальном уравнении. Примеры задач, приводящих к дифференциальным уравнениям.

    18. Обыкновенное дифференциальное уравнение. Общее и частное решение Дифференциального уравнения.

    19. Основные понятия комбинаторики: размещения, перестановки, сочетания

    20. Основные понятия и методы теории вероятностей: случайные события и их вероятности. Классическое определение вероятности.

    Практическая часть
    Задание 1.

    Проверяемые результаты обучения: З.1
    1. Вычислить предел: .

    2. Вычислить предел: .

    3. Вычислить предел: .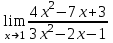

    4. Вычислить предел: .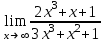

    5. Вычислить предел: .

    6. Вычислить предел: .

    7. Вычислить предел: .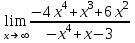

    8. Вычислить предел: .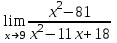

    9. Вычислить предел: .

    10. Вычислить предел: .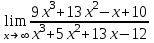
    Задание 2.

    Проверяемые результаты обучения: З.1

    1. Найдите промежутки возрастания и экстремумы функции .

    2. Найдите промежутки возрастания и экстремумы функции .

    3. Найдите промежутки возрастания и экстремумы функции .

    4. Найдите промежутки убывания и экстремумы функции .

    5. Найдите промежутки убывания и экстремумы функции .

    6. Найдите промежутки убывания и экстремумы функции .

    7. Найдите промежутки возрастания и экстремумы функции .

    8. Найдите промежутки убывания и экстремумы функции .

    9. Найдите промежутки убывания и экстремумы функции .

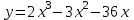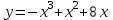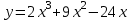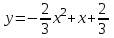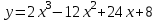    10. Найдите промежутки возрастания и экстремумы функции .


    Задание 3

    Проверяемые результаты обучения: З.1

    1. Найдите интеграл:

    2. Найти интеграл:

    3. Найти интеграл:

    4. Найти интеграл:

    5. Найти интеграл:

    6. Найдите интеграл:

    7. Найдите интеграл:

    8. Найдите интеграл:

    9. Найдите интеграл:

    10. Найдите интеграл:

    Задание 4.

    Проверяемые результаты обучения: З.1

    1. Найдите площадь фигуры, ограниченной линиями: y = - x2 + x + 6 и y = 0.

    2. Найдите площадь фигуры, ограниченной линиями: y = x2 +5x + 6, прямыми x = -1, x = 2 и осью абсцисс.

    3. Найдите площадь фигуры, ограниченной линиями: y = - x2 +2x + 3 иy = 0

    4. Найдите площадь фигуры, ограниченной линиями: y = x2 - 8x + 18, x = 2, x = 6 иy = 0.

    5. Найдите площадь фигуры, ограниченной линиями: y = - x2 + 10x – 16 иy = 0.

    6. Найдите площадь фигуры, ограниченной линиями: y = x2 +8x + 16 ипрямойx = =2.

    7. Найдите площадь фигуры, ограниченной линиями: y = - x2 +4 ипрямой y = 0. x=-2, x=2.

    8. Найдите площадь фигуры, ограниченной линиями: y = - x2 +1 ипрямой y = 0. x=-1, x=1.

    9. Найдите площадь фигуры, ограниченной линиями: иy = 0

    10. Найдите площадь фигуры, ограниченной линиями: иy = 0.


    Задание 5.

    Проверяемые результаты обучения: У.1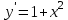

    1. Найдите общее решение дифференциального уравнения:

    2. Найдите общее решение дифференциального уравнения:

    3. Найдите общее решение дифференциального уравнения:

    4. Найдите общее решение дифференциального уравнения:

    5. Найдите общее решение дифференциального уравнения:

    6. Найдите общее решение дифференциального уравнения:

    7. Найдите общее решение дифференциального уравнения:

    8. Найдите общее решение дифференциального уравнения:

    9. Найдите общее решение дифференциального уравнения:

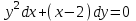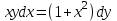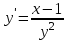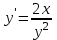    10. Найдите общее решение дифференциального уравнения:


    Задание 6.

    Проверяемые результаты обучения: З.1

    1. В ящике в случайном порядке разложены 20 деталей, причем пять из них стандартные. Рабочий берет наудачу три детали. Найдите вероятность того, что одна деталь окажется стандартной.

    2. В партии из 30 пар обуви имеется 10 пар мужской, 8 пар женской и 12 пар детской обуви. Продавец выбирает наудачу три пары обуви. Найдите вероятность того, что выбранная пара окажется женской.

    3. В урне находятся 10 пронумерованных шаров красного цвета и 6 пронумерованных шаров желтого цвета. Какова вероятность того, что наудачу извлеченный шар окажется красного цвета.

    4. В урне находится 10 белых, 15 черных и 20 синих шаров. Найдите вероятность того, что вынутый наудачу один шар окажется черным.

    5. В спортивном зале мячи в корзине находятся 3 волейбольных, 1 футбольный и 5 баскетбольных мячей. Тренер достает один мяч на удачу. Какова вероятность того, что этот мяч окажется баскетбольным.

    6. В урне находится 10 белых, 15 черных и 20 синих шаров. Найдите вероятность того, что вынутый на удачу шар окажется черным.

    7. В урне находится 15 белых, 20 черных и 30 синих шаров. Найдите вероятность того, что вынутый наудачу шар окажется синим.

    8. Бросаются две игральные кости. Найдите вероятность того, что сумма очков, выпавших на двух костях, окажется равной 8?

    9. В корзине находятся 20 шаров: 5 синих, 4 красных, остальные черные. Выбирают наудачу один шар. Определить с какой вероятностью он будет цветным.

    10. Витя забыл две последние цифры номера телефона приятеля и набрал их наугад. С какой вероятностью этот звонок попадет к приятелю?

    написать администратору сайта