ВКР Рынок жилья. Заключение 45

Название	Заключение 45
Дата	11.04.2018
Размер	316.47 Kb.
Формат файла
Имя файла	ВКР Рынок жилья.docx
Тип	Реферат #40876
страница	3 из 6

1 2 3 4 5 6

ГЛАВА 3. МОДЕЛИРОВАНИЕ СРЕДНЕЙ ЦЕНЫ ЗА КВАДРАТНЫЙ МЕТР НА ПЕРВИЧНОМ РЫНКЕ ЖИЛЬЯ ГОРОДА МОСКВЫ

3.1 Корреляционно-регрессионный анализ факторов, влияющих на среднюю цену за квадратный метр на первичном рынке жилья города Москвы без учета программы реновации пятиэтажек

Примем среднюю цену за кв.м. за результативный признак – Y.

Рассмотрим влияние на среднюю цену следующих факторов:

Х1 – Располагаемые ресурсы домашних хозяйств в среднем на члена домашнего хозяйства в месяц, рублей;

Х2 – Общая площадь жилищного фонда, млн кв. м;

Х3 – Число квартир, тыс. ед.;

Х4 – ВРП на душу населения, тыс. руб.;

Х5 – Ввод в действие жилых домов, тыс. кв. м;

По этим данным построим регрессионную модель и проведем оценку её качества.

Проведем корреляционный анализ, включая проверку теста мультиколлинеарность факторов.

Построим матрицу коэффициентов парной корреляции для всех факторов модели.

Таблица 5.

Матрица коэффициентов парной корреляции для всех факторов модели

-	y	x1	x2	x3	x4	x5
y	1	0.922	0.892	0.9066	0.9533	-0.7038
x1	0.922	1	0.984	0.9846	0.9792	-0.6946
x2	0.892	0.984	1	0.9992	0.9605	-0.6003
x3	0.9066	0.9846	0.9992	1	0.966	-0.6023
x4	0.9533	0.9792	0.9605	0.966	1	-0.6749
x5	-0.7038	-0.6946	-0.6003	-0.6023	-0.6749	1

В нашем случае между следующими показателями:

r_x1x₂– Располагаемые ресурсы домашних хозяйств в среднем на члена домашнего хозяйства в месяц и Общая площадь жилищного фонда

r_x1x₃– Располагаемые ресурсы домашних хозяйств в среднем на члена домашнего хозяйства в месяц и Число квартир

r_x1x₄– Располагаемые ресурсы домашних хозяйств в среднем на члена домашнего хозяйства в месяц и ВРП на душу населения

r_x2x₁ – Общая площадь жилищного фонда и Располагаемые ресурсы домашних хозяйств в среднем на члена домашнего хозяйства в месяц

r_x2x₃ – Общая площадь жилищного фонда и Число квартир

r_x2x₄ – Общая площадь жилищного фонда и ВРП на душу населения

r_x3x₁ – Число квартир и Располагаемые ресурсы домашних хозяйств в среднем на члена домашнего хозяйства в месяц

r_x3x₂ – Число квартир и Общая площадь жилищного фонда

r_x3x₄ – Число квартир и ВРП на душу населения

r_x4x₁ – ВРП на душу населения и

r_x4x₂ – ВРП на душу населения и Общая площадь жилищного фонда

r_x4x₃ – ВРП на душу населения и Число квартир

имеют |r|>0.7, что говорит о мультиколлинеарности факторов и о необходимости исключения одного из них из дальнейшего анализа.

Проверим значимость полученных парных коэффициентов корреляции с помощью t-критерия Стьюдента. Коэффициенты, для которых значения t-статистики по модулю больше найденного критического значения, считаются значимыми.

Рассчитаем наблюдаемые значения t-статистики для r_yx₁по формуле: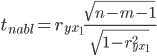

$https://chart.googleapis.com/chart?cht=tx&chl=t_%7bnabl%7d%20=%20r_%7byx_%7b1%7d%7d%20\frac%7b\sqrt%7bn-m-1%7d%7d%7b\sqrt%7b1%20-%20r_%7byx_%7b1%7d%7d%5e%7b2%7d%7d%7d$ (17)

где m = 1 - количество факторов в уравнении регрессии.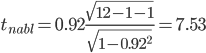

$https://chart.googleapis.com/chart?cht=tx&chl=t_%7bnabl%7d%20=%200.92%20\frac%7b\sqrt%7b12%20-%201%20-%201%7d%7d%7b\sqrt%7b1%20-%200.92%5e%7b2%7d%7d%7d%20=%207.53$ (18)

По таблице Стьюдента находим Tтабл: t_крит(n-m-1;α/2)=(10;0.025)=2.228.
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.

Рассчитаем наблюдаемые значения t-статистики для r_yx₂по формуле: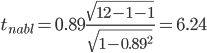

$https://chart.googleapis.com/chart?cht=tx&chl=t_%7bnabl%7d%20=%200.89%20\frac%7b\sqrt%7b12%20-%201%20-%201%7d%7d%7b\sqrt%7b1%20-%200.89%5e%7b2%7d%7d%7d%20=%206.24$ (19)

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.

Рассчитаем наблюдаемые значения t-статистики для r_yx3по формуле: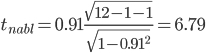

$https://chart.googleapis.com/chart?cht=tx&chl=t_%7bnabl%7d%20=%200.91%20\frac%7b\sqrt%7b12%20-%201%20-%201%7d%7d%7b\sqrt%7b1%20-%200.91%5e%7b2%7d%7d%7d%20=%206.79$ (20)

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.

Рассчитаем наблюдаемые значения t-статистики для r_yx4по формуле: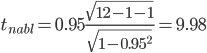

$https://chart.googleapis.com/chart?cht=tx&chl=t_%7bnabl%7d%20=%200.95%20\frac%7b\sqrt%7b12%20-%201%20-%201%7d%7d%7b\sqrt%7b1%20-%200.95%5e%7b2%7d%7d%7d%20=%209.98$ (21)

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.

Рассчитаем наблюдаемые значения t-статистики для r_yx5по формуле: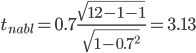

$https://chart.googleapis.com/chart?cht=tx&chl=t_%7bnabl%7d%20=%200.7%20\frac%7b\sqrt%7b12%20-%201%20-%201%7d%7d%7b\sqrt%7b1%20-%200.7%5e%7b2%7d%7d%7d%20=%203.13$ (22)

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.

Таким образом, связь между (y и x_x1), (y и x_x2), (y и x_x3), (y и x_x4), (y и x_x5) является существенной.

В нашем случае (y и x_x1 ), (y и x_x2 ), (y и x_x3 ), (y и x_x4 ), имеют |r|>0.7, что говорит о мультиколлинеарности факторов и о необходимости исключения одного из них из дальнейшего анализа.

Проверим переменные на мультиколлинеарность методом Фаррара-Глоубера по первому виду статистических критериев (критерий "хи-квадрат").
Формула для расчета значения статистики Фаррара-Глоубера:

χ² =-[n-1-(2m+5)/6]ln(det[R])=-[12-1-(2*5+5)/6]ln(0)=156.93 (23)

где m = 5 - количество факторов,

n = 12 - количество наблюдений,

det[R] - определитель матрицы парных коэффициентов корреляции R.

Сравниваем его с табличным значением при v = m/2(m-1) = 10 степенях свободы и уровне значимости α. Если χ² > χ_табл², то в векторе факторов присутствует мультиколлинеарность.

χ_табл²(10;0.05) = 18.30704

Проверим переменные на мультиколлинеарность по второму виду статистических критериев (критерий Фишера).

Определяем обратную матрицу D = R^-1:

Таблица 6.

Обратная матрица D = R^-1

42.5054	-5.222	293.0633	-305.5077	-17.3982	6.4651
-5.222	109.3911	-164.6874	102.9282	-35.7674	11.2971
293.0633	-164.6873	2937.4081	-3005.6379	-10.3132	37.9464
-305.5077	102.9281	-3005.6379	3134.7065	16.0988	-48.9165
-17.3982	-35.7674	-10.3132	16.0988	44.6255	-3.4653
6.4651	11.2971	37.9464	-48.9165	-3.4653	4.3748

Вычисляем F-критерии Фишера:

$https://chart.googleapis.com/chart?cht=tx&chl=f_%7bk%7d%20=%20(d_%7bkk%7d-1)\frac%7bn-m%7d%7bm-1%7d$ (24)

где d_kk - диагональные элементы матрицы.

Рассчитанные значения критериев сравниваются с табличными при v₁=n-m и v₂=m-1 степенях свободы и уровне значимости α. Если F_k > F_Табл, то k-я переменная мультиколлинеарна с другими.

v₁=12-5 = 8; v₂=5-1 = 5. F_Табл(8;5) = 4.82

$https://chart.googleapis.com/chart?cht=tx&chl=f_%7b1%7d%20=%20(42.505-1)\frac%7b12-5%7d%7b5-1%7d%20=%2066.41$ (25)

Поскольку F₁ > F_табл, то переменная y мультиколлинеарна с другими.

$https://chart.googleapis.com/chart?cht=tx&chl=f_%7b2%7d%20=%20(109.391-1)\frac%7b12-5%7d%7b5-1%7d%20=%20173.43$ (26)

Поскольку F₂ > F_табл, то переменная x₁ мультиколлинеарна с другими.

$https://chart.googleapis.com/chart?cht=tx&chl=f_%7b3%7d%20=%20(2937.408-1)\frac%7b12-5%7d%7b5-1%7d%20=%204698.25$ (27)

Поскольку F₃ > F_табл, то переменная x₂ мультиколлинеарна с другими.

$https://chart.googleapis.com/chart?cht=tx&chl=f_%7b4%7d%20=%20(3134.707-1)\frac%7b12-5%7d%7b5-1%7d%20=%205013.93$ (28)

Поскольку F₄ > F_табл, то переменная x₃ мультиколлинеарна с другими.

$https://chart.googleapis.com/chart?cht=tx&chl=f_%7b5%7d%20=%20(44.626-1)\frac%7b12-5%7d%7b5-1%7d%20=%2069.8$ (29)

Поскольку F₅ > F_табл, то переменная x₄ мультиколлинеарна с другими.

$https://chart.googleapis.com/chart?cht=tx&chl=f_%7b6%7d%20=%20(4.375-1)\frac%7b12-5%7d%7b5-1%7d%20=%205.4$ (30)

Поскольку F₆ > F_табл, то переменная x₅ мультиколлинеарна с другими.

Проверим переменные на мультиколлинеарность по третьему виду

статистических критериев (критерий Стьюдента). Для этого найдем частные коэффициенты корреляции. На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.
Таблица 7.

Частные коэффициенты корреляции

Переменные	Коэффициент	Теснота связи
x1/x2	0.55	Умеренная
x1/x3	0.398	Не сильная
x1/x4	-0.188	Низкая
x1/x5	0.848	Сильная
x2/x1	-0.221	Низкая
x2/x3	-0.795	Сильная
x2/x4	-0.281	Низкая
x2/x5	0.826	Сильная
x3/x1	-0.0184	Низкая
x3/x2	0.824	Сильная
x3/x4	-0.184	Низкая
x3/x5	0.851	Сильная
x4/x1	0.643	Умеренная
x4/x2	0.767	Сильная
x4/x3	0.711	Сильная
x4/x5	0.912	Сильная
x5/x1	-0.227	Низкая
x5/x2	-0.465	Не сильная
x5/x3	-0.468	Не сильная
x5/x4	-0.271	Низкая
x1x2/y	0.923	Сильная
x1x2/x3	0.0267	Низкая
x1x2/x4	0.77	Сильная
x1x2/x5	0.986	Сильная
x1x3/y	0.91	Сильная
x1x3/x2	0.201	Низкая
x1x3/x4	0.738	Сильная
x1x3/x5	0.986	Сильная
x1x4/y	0.858	Сильная
x1x4/x2	0.688	Умеренная
x1x4/x3	0.621	Умеренная
x1x4/x5	0.962	Сильная
x1x5/y	-0.166	Низкая
x1x5/x2	-0.729	Сильная
x1x5/x3	-0.728	Сильная
x1x5/x4	-0.225	Низкая
x2x3/y	0.998	Сильная
x2x3/x1	0.973	Сильная
x2x3/x4	0.991	Сильная
x2x3/x5	0.999	Сильная
x2x4/y	0.807	Сильная
x2x4/x1	-0.0848	Низкая
x2x4/x3	-0.444	Не сильная
x2x4/x5	0.941	Сильная
x2x5/y	0.0855	Низкая
x2x5/x1	0.649	Умеренная
x2x5/x3	0.0451	Низкая
x2x5/x4	0.233	Низкая
x3x4/y	0.799	Сильная
x3x4/x1	0.0522	Низкая
x3x4/x2	0.555	Умеренная
x3x4/x5	0.95	Сильная
x3x5/y	0.119	Низкая
x3x5/x1	0.65	Умеренная
x3x5/x2	-0.076	Низкая
x3x5/x4	0.26	Низкая
x4x5/y	-0.0185	Низкая
x4x5/x1	0.0361	Низкая
x4x5/x2	-0.442	Не сильная
x4x5/x3	-0.451	Не сильная

Можно сделать вывод, что при построении регрессионного уравнения следует отобрать факторы x₁, x₂, x₃, x₄ .

1 2 3 4 5 6