эконометрика. Контрольная работа по дисциплине Эконометрика
 Скачать 152.32 Kb. Скачать 152.32 Kb.
|
|
Министерство науки и высшего образования РФ ФГБОУ ВО «Псковский государственный университет» Институт права, экономики и управления Кафедра экономики, финансов и финансового права КОНТРОЛЬНАЯ работа по дисциплине «Эконометрика» Вариант №2 Выполнил студент: Гаврилов В.В. Группа:0072-04 Преподаватель: Кистаева Н. Н. Псков 2021 Содержание 1 задание ………………………………………………………………………………… 3 2 задание ………………………………………………………………………………… 19 Задание 1 Решение Исходные данные для анализа представлены в таблице 1.1: Таблица 1.1 – исходные данные
Воспользуемся пакетом анализа данных «Excel» (инструмент «Корреляция») для расчета коэффициентов интеркорреляции. Записываем их в виде матрицы (таб.1.2) Таблица 1.2- Матрица коэффициентов парной корреляции
Так как rx1x2 = 0,950, то между факторами присутствует мультиколлинеарность. С помощью пакета анализа Excel вычислены значения выборочных средних и среднеквадратических отклонений для изучаемых переменных (таб. 1.2) Таблица 1.2 – Промежуточные расчеты для построения регрессии
Вывод : Факторы тесно коррелированы между собой. Линейное уравнение множественной регрессии y от x1 и x2 имеет вид: 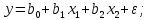 Искомое уравнение в стандартизованном масштабе: 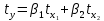 , ,где 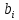 — коэффициенты «чистой регресии»; — коэффициенты «чистой регресии»;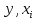 — переменные исходной модели, — переменные исходной модели,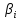 – стандартизованные коэффициенты регрессии, – стандартизованные коэффициенты регрессии,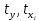 – стандартизованные переменные, – стандартизованные переменные, 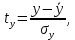 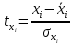 Расчет 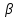 - коэффициентов выполнен по формулам: - коэффициентов выполнен по формулам: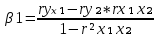 = = 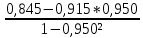 = -0,243 = -0,243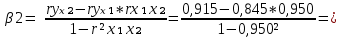 1,146 1,146Уравнение в стандартизованном масштабе: ty = 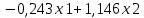 Вывод: x2 оказывает на y более сильное влияние, чем x1 Для построения уравнения в естественной форме необходимо рассчитать 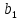 и и 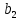 , используя формулы перехода от , используя формулы перехода от 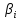 к к 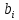 : :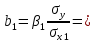 -3,07 -3,07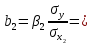 0,46 0,46Значение α находим по следующей формуле: 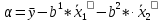 15388,070 15388,070Уравнение в естественном виде выглядит следующим образом: 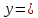 15388,07-3,067x1+0,455x2 15388,07-3,067x1+0,455x2Результаты регрессионного анализа представлены в таблице 1.4: Таблица 1.4 – Результаты регрессионного анализа
Исходя из результатов анализа, представленных в таблице 1.4, можно сделать следующие выводы. Вывод: Линейная модель адекватна для исходных данных, связь прямая и тесная (Множественный R = 0,92) R2 = 84% вариации средних цен на первичном рынке жилья на конец год объяснено определяются вариацией учтенных в модели факторов: среднегодовая численность населения и объем жилищных кредитов. F = 104,68 уравнение в целом значимо (α=0,05) Значение показатели Fкритич считаем с помощью формулы «Excel» - формула «F.ОБР.ПХ.» Fкритич =3,238 Оба коэффициента регрессии значимы (α = 0,05), не значим свободный член Частные коэффициенты эластичности: Эyx1 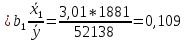 Эyx2 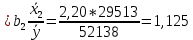 Вывод: При увеличении среднегодовая численность населения на 1% от ее среднего уровня, средние цены на первичном рынке жилья уменьшиться на 0,11% от ее среднего уровня, а при увеличении объем жилищных кредитов, предоставленных кредитными организациями физическим лицам на 1% от ее среднего уровня, средние цены на первичном рынке жилья увеличиться на 0,32% от ее среднего уровня. Фактор x2 сильнее влияет на y, чем x1. Такие же выводы можно сделать при сравнении 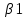 и и 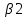 . .Различия в силе влияния факторов на результат, полученные при сравнении 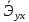 и и 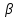 объясняются тем, что коэффициент эластичности исходит из соотношения средних, а объясняются тем, что коэффициент эластичности исходит из соотношения средних, а 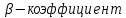 из соотношения квадратичных отклонений. из соотношения квадратичных отклонений.Линейные коэффициенты частной корреляции: 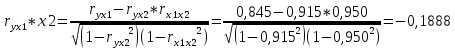 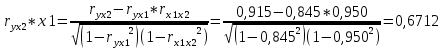 Сравниваем полученные результаты линейных коэффициентов частной корреляции и приходим к выводу, что объем жилищных кредитов, предоставленных кредитными организациями физическим лицам, имеет более тесную связь со средние цены на первичном рынке жилья, чем среднегодовая численность населения. Частный F-критерий: 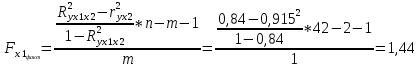 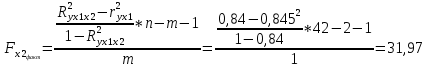 Вывод: Низкое значение 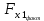 свидетельствует о статистической незначимости прироста свидетельствует о статистической незначимости прироста 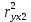 за счёт включение в модель фактора среднегодовая численность населения. Следовательно, подтверждается нулевая гипотеза за счёт включение в модель фактора среднегодовая численность населения. Следовательно, подтверждается нулевая гипотеза 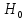 о нецелесообразности включения его в модель. о нецелесообразности включения его в модель. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
