Таблица 1.13 – Регрессионный анализ
Регрессионная статистика
|
|
|
|
|
|
|
|
Множественный R
|
0,95
|
|
|
|
|
|
|
|
R-квадрат
|
0,90
|
|
|
|
|
|
|
|
Нормированный R-квадрат
|
0,89
|
|
|
|
|
|
|
|
Стандартная ошибка
|
13366,92
|
|
|
|
|
|
|
|
Наблюдения
|
18
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
Регрессия
|
2
|
24322781693
|
12161390847
|
68,06443535
|
2,98936E-08
|
|
|
|
Остаток
|
15
|
2680120121
|
178674674,7
|
|
|
|
|
|
Итого
|
17
|
27002901814
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
42185,64
|
5355,95
|
7,88
|
0,00
|
30769,71
|
53601,57
|
30769,71
|
53601,57
|
Переменная X 1
|
-5,02
|
3,69
|
-1,36
|
0,19
|
-12,88
|
2,84
|
-12,88
|
2,84
|
Переменная X 2
|
0,52
|
0,11
|
4,63
|
0,00
|
0,28
|
0,75
|
0,28
|
0,75
|
Расчет значений:
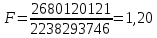
Расчет знамения Fкритич с помощью функции Excel «F.ОБР.ПХ»:
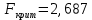
Вывод:
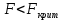 , Гипотеза H0 о гомоскедастичности остатков принимается. , Гипотеза H0 о гомоскедастичности остатков принимается.
Теперь проверим тест ранговой корреляции Спирмена.
Таблица 1.14 – Промежуточные расчеты для теста Спирмена
Характеристики для ранжирования
|
Ранги
|
квадрат разностей рангов di²
|
ІɛІ
|
х1
|
ІɛІ
|
х1
|
12561,2
|
1548,3
|
35
|
31
|
16
|
8127,3
|
1196,3
|
31
|
25
|
36
|
11055,2
|
1362,1
|
34
|
28
|
36
|
1486,8
|
2326,0
|
4
|
34
|
900
|
4289,0
|
1000,7
|
20
|
15
|
25
|
3070,5
|
1006,0
|
13
|
16
|
9
|
3868,4
|
635,3
|
17
|
9
|
64
|
2831,5
|
1105,5
|
10
|
20
|
100
|
21,4
|
1141,7
|
1
|
23
|
484
|
39482,3
|
7645,2
|
42
|
40
|
4
|
4352,4
|
736,5
|
21
|
11
|
100
|
3492,6
|
1111,5
|
15
|
21
|
36
|
5055,3
|
938,6
|
22
|
14
|
64
|
6463,8
|
1011,4
|
25
|
19
|
36
|
687,4
|
1265,0
|
3
|
27
|
576
|
6968,5
|
1472,5
|
28
|
30
|
4
|
8020,8
|
1256,5
|
30
|
26
|
16
|
21831,3
|
12646,7
|
39
|
41
|
4
|
8260,9
|
616,1
|
32
|
7
|
625
|
2695,5
|
825,4
|
9
|
12
|
9
|
12758,5
|
1140,3
|
36
|
22
|
196
|
4122,3
|
1164,1
|
18
|
24
|
36
|
6219,0
|
1007,3
|
24
|
17
|
49
|
3003,1
|
1861,8
|
12
|
32
|
400
|
1783,5
|
598,4
|
5
|
6
|
1
|
4245,4
|
627,9
|
19
|
8
|
121
|
7366,9
|
5391,0
|
29
|
38
|
81
|
2642,6
|
458,9
|
7
|
3
|
16
|
13007,4
|
271,9
|
37
|
1
|
1296
|
27300,7
|
1912,2
|
40
|
33
|
49
|
6469,1
|
5661,8
|
26
|
39
|
169
|
3836,4
|
1009,9
|
16
|
18
|
4
|
2925,2
|
2499,3
|
11
|
35
|
576
|
3403,1
|
4200,1
|
14
|
37
|
529
|
29167,3
|
446,2
|
41
|
2
|
1521
|
2471,7
|
3098,5
|
6
|
36
|
900
|
177,4
|
502,2
|
2
|
5
|
9
|
17896,9
|
867,3
|
38
|
13
|
625
|
2647,0
|
465,6
|
8
|
4
|
16
|
6508,9
|
698,1
|
27
|
10
|
289
|
8899,2
|
1467,8
|
33
|
29
|
16
|
6055,5
|
2799,4
|
23
|
36
|
169
|
Представим расчеты показателей:
Коэффициент ранговой корреляции:
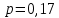
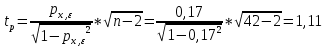
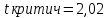
Вывод:
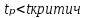 , H0 о гомоскедастичности не отклоняется, принимается гипотеза об отсутствии гетероскедастичности. , H0 о гомоскедастичности не отклоняется, принимается гипотеза об отсутствии гетероскедастичности.
H1 гетероскедастичность отсутствует.
Промежуточные данные представлены в таб.1.15:
Таблица 1.15 - Промежуточные расчеты для теста Спирмена
Характеристики для ранжирования
|
Ранги
|
квадрат разностей рангов di²
|
ІɛІ
|
х2
|
ІɛІ
|
х2
|
12561,2
|
19733
|
34
|
27
|
49
|
8127,3
|
16821
|
30
|
22
|
64
|
11055,2
|
21384
|
33
|
29
|
16
|
1486,8
|
36490
|
4
|
35
|
961
|
4289,0
|
12221
|
20
|
15
|
25
|
3070,5
|
22749
|
13
|
30
|
289
|
3868,4
|
9168
|
17
|
11
|
36
|
2831,5
|
15838
|
10
|
21
|
121
|
21,4
|
15812
|
1
|
20
|
361
|
39482,3
|
242590
|
41
|
40
|
1
|
4352,4
|
12320
|
21
|
16
|
25
|
3492,6
|
20386
|
15
|
28
|
169
|
5055,3
|
14315
|
22
|
19
|
9
|
6463,8
|
14053
|
24
|
18
|
36
|
687,4
|
23912
|
3
|
31
|
784
|
6968,5
|
25645
|
27
|
32
|
25
|
8020,8
|
18200
|
29
|
23
|
36
|
21831,3
|
393629
|
38
|
41
|
9
|
8260,9
|
11264
|
31
|
13
|
324
|
2695,5
|
19411
|
9
|
25
|
256
|
12758,5
|
26500
|
35
|
33
|
4
|
4122,3
|
19696
|
18
|
26
|
64
|
6219,0
|
18366
|
23
|
24
|
1
|
3003,1
|
45525
|
12
|
36
|
576
|
1783,5
|
9337
|
5
|
12
|
49
|
4245,4
|
8439
|
19
|
9
|
100
|
7366,9
|
195015
|
28
|
39
|
121
|
2642,6
|
4103
|
7
|
5
|
4
|
13007,4
|
5365
|
36
|
6
|
900
|
27300,7
|
8852
|
39
|
10
|
841
|
6469,1
|
77706
|
25
|
38
|
169
|
3836,4
|
13682
|
16
|
17
|
1
|
2925,2
|
34769
|
11
|
34
|
529
|
3403,1
|
59165
|
14
|
37
|
529
|
29167,3
|
3011
|
40
|
3
|
1369
|
2471,7
|
11715
|
6
|
14
|
64
|
177,4
|
397
|
2
|
1
|
1
|
17896,9
|
6120
|
37
|
8
|
841
|
2647,0
|
3292
|
8
|
4
|
16
|
6508,9
|
5984
|
26
|
7
|
361
|
8899,2
|
2568
|
33
|
2
|
961
|
6055,5
|
32461
|
23
|
34
|
121
|
Расчеты значений:
Коэффициент ранговой корреляции:
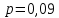
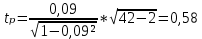
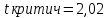
Вывод:
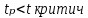 , H0 о гомоскедастичности не отклоняется, принимается гипотеза об отсутствии гетероскедастичности. , H0 о гомоскедастичности не отклоняется, принимается гипотеза об отсутствии гетероскедастичности.
|
 Скачать 152.32 Kb.
Скачать 152.32 Kb.
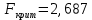
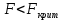 , Гипотеза H0 о гомоскедастичности остатков принимается.
, Гипотеза H0 о гомоскедастичности остатков принимается.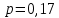
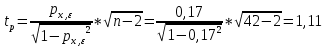
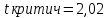
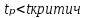 , H0 о гомоскедастичности не отклоняется, принимается гипотеза об отсутствии гетероскедастичности.
, H0 о гомоскедастичности не отклоняется, принимается гипотеза об отсутствии гетероскедастичности.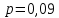
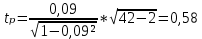
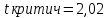
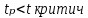 , H0 о гомоскедастичности не отклоняется, принимается гипотеза об отсутствии гетероскедастичности.
, H0 о гомоскедастичности не отклоняется, принимается гипотеза об отсутствии гетероскедастичности.