Задание 2
Заносим исходные данные по Валовой добавленной стоимости в основных ценах за 2015-2018 гг. в табл. 2.1.
Таблица 2.1. - Исходные данные о валовой добавленной стоимости в основных ценах за 2015-2018 гг.
2015
|
I квартал
|
388,7
|
II квартал
|
571,7
|
III квартал
|
1 349,10
|
IV квартал
|
908,5
|
2016
|
I квартал
|
417,6
|
II квартал
|
594,4
|
III квартал
|
1 368,20
|
IV квартал
|
907,7
|
2017
|
I квартал
|
436,2
|
II квартал
|
603,6
|
III квартал
|
1 360,60
|
IV квартал
|
863,4
|
2018
|
I квартал
|
456,8
|
II квартал
|
634,4
|
III квартал
|
1 417,90
|
IV квартал
|
1 016,30
|
Строим график данного временного ряда (рис.2.1)
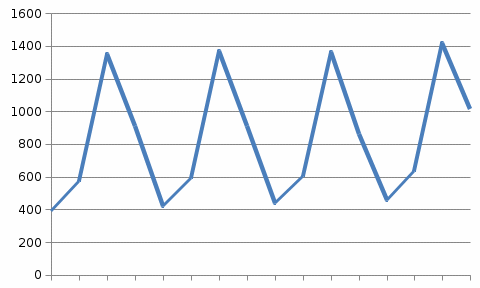
Рисунок 2.1- Временной ряд валовой добавленной стоимости в основных ценах за 2015-2018 гг.
Дальше требуется определить коэффициенты автокорреляции различных порядков.
Для этого необходимо добавить значения yt-1, yt-2, yt-3, yt-4 и т.д. (табл. 2.2)
№
|
yt
|
yt1
|
yt2
|
yt3
|
yt4
|
1
|
388,7
|
-
|
-
|
-
|
-
|
2
|
571,7
|
388,7
|
-
|
-
|
-
|
3
|
1 349,10
|
571,7
|
388,7
|
-
|
-
|
4
|
908,5
|
1 349,10
|
571,7
|
388,7
|
-
|
5
|
417,6
|
908,5
|
1 349,10
|
571,7
|
388,7
|
6
|
594,4
|
417,6
|
908,5
|
1 349,10
|
571,7
|
7
|
1 368,20
|
594,4
|
417,6
|
908,5
|
1 349,10
|
8
|
907,7
|
1 368,20
|
594,4
|
417,6
|
908,5
|
9
|
436,2
|
907,7
|
1 368,20
|
594,4
|
417,6
|
10
|
603,6
|
436,2
|
907,7
|
1 368,20
|
594,4
|
11
|
1 360,60
|
603,6
|
436,2
|
907,7
|
1 368,20
|
12
|
863,4
|
1 360,60
|
603,6
|
436,2
|
907,7
|
13
|
456,8
|
863,4
|
1 360,60
|
603,6
|
436,2
|
14
|
634,4
|
456,8
|
863,4
|
1 360,60
|
603,6
|
15
|
1 417,90
|
634,4
|
456,8
|
863,4
|
1 360,60
|
16
|
1 016,30
|
1 417,90
|
634,4
|
456,8
|
863,4
|
лаг t
|
1
|
2
|
3
|
4
|
5
|
автокорреляция
|
0,01
|
-0,91
|
-0,06
|
0,99
|
Коэффициенты корреляции различных порядков были рассчитаны с использованием функции КОРРЕЛ в «Excel». Построим коррелограмму данного ряда (рис. 2.2)
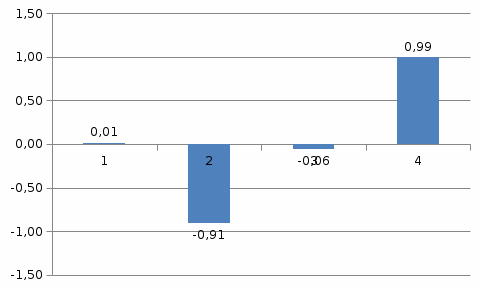
Рисунок 2.2 – Коррелограмма.
Из представленной коррелограммы можно сделать вывод, что валовой добавленной стоимости в основных ценах характеризуется сезонностью периодичностью в четыре квартала.
Построим аддитивную и мультипликативные модели временного ряда.
#
|
yt
|
Скользящая средняя за 4 квартала
|
центрированная скользящая средняя
|
оценки сезон компоненты
|
1
|
388,7
|
-
|
-
|
-
|
2
|
571,7
|
804,5
|
-
|
-
|
3
|
1 349,10
|
811,7
|
808,1
|
541,0
|
4
|
908,5
|
817,4
|
814,6
|
93,9
|
5
|
417,6
|
822,2
|
819,8
|
-402,2
|
6
|
594,4
|
822,0
|
822,1
|
-227,7
|
7
|
1 368,20
|
826,6
|
824,3
|
543,9
|
8
|
907,7
|
828,9
|
827,8
|
79,9
|
9
|
436,2
|
827,0
|
828,0
|
-391,8
|
10
|
603,6
|
816,0
|
821,5
|
-217,9
|
11
|
1 360,60
|
821,1
|
818,5
|
542,1
|
12
|
863,4
|
828,8
|
825,0
|
38,4
|
13
|
456,8
|
843,1
|
836,0
|
-379,2
|
14
|
634,4
|
881,4
|
862,2
|
-227,8
|
15
|
1 417,90
|
-
|
-
|
-
|
16
|
1 016,30
|
-
|
-
|
-
|
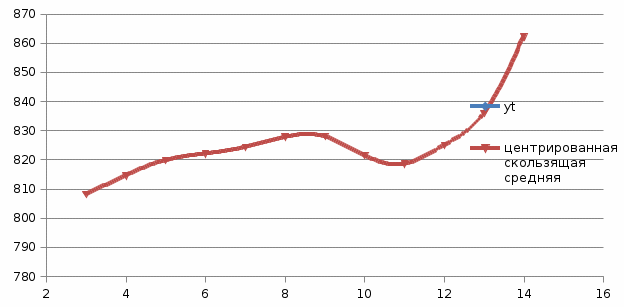
Построим график, отражающий ряд исходных данных и выровненный ряд, показывающий рассчитанные центрированные скользящие средние (рис. 2.3).
|
 Скачать 152.32 Kb.
Скачать 152.32 Kb.


