эконометрика. Контрольная работа по дисциплине Эконометрика
 Скачать 152.32 Kb. Скачать 152.32 Kb.
|
|
Таблица 2.7- Расчёт значений сезонной компоненты в мультипликативной модели.
Корректирующий коэффициент k для данной модели рассчитывается по формуле : 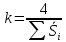 , ,где k — корректирующий коэффициент, 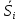 — средняя оценка сезонной компоненты для i-ого квартала. — средняя оценка сезонной компоненты для i-ого квартала.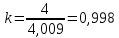 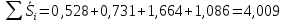 Рассчитаем скорректированные значения сезонной компоненты как произведение между ее средними оценками и корректирующим коэффициентом: I квартал: S1 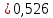 ; ;II квартал: S2 = 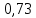 ; ;III квартал: S3 = 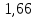 ; ;IV квартал: S4 = 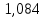 . .Далее производим выравнивание значений сезонной компоненты (табл. 2.8). Таблица 2.8- Расчет выравненных значений T и ошибок Е в мультипликативной модели.
Для определения компоненты Т данной модели рассчитаем параметры линейного тренда T=a + bt 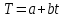 где 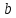 — коэффициент регрессии, — коэффициент регрессии,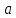 — константа. — константа.Находим параметры трендовой компоненты с использованием статистической функции Excel ЛИНЕЙН: 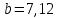 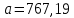 Таким образом, имеем следующий линейный тренд: 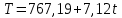 Оцениваем качество построения модели путем расчета R2 , которое можно найти по формуле 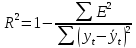 где 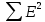 — сумма квадратов случайной компоненты, — сумма квадратов случайной компоненты,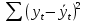 — сумма квадратов отклонений уровней ряда от его среднего уровня. — сумма квадратов отклонений уровней ряда от его среднего уровня.Либо с помощью статистической функции Exel ДИСП.Г. по формуле 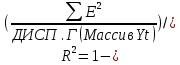 16) 16)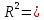 0,9929 0,9929Это означает, что мультипликативная модель объясняет 99,29% общей вариации уровней исследуемого временного ряда. 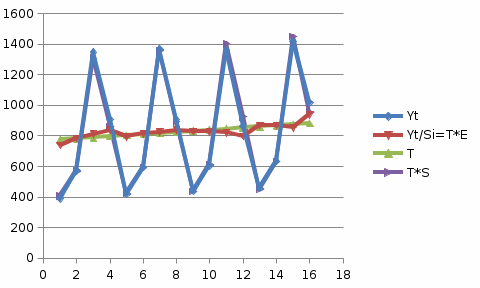 Рисунок 2.6 - Соответствие результатов моделирования исходным данным для мультипликативной модели. Из графика видно, что рассчитанные значения T*S почти не отличаются от фактических значений. Это подтверждает, что в мультипликативной модели доля объясненной вариации уровней очень высокая. Поскольку доля объясненной вариации уровней ряда для мультипликативной модели больше, то она является лучшей, поэтому прогноз следует сделать на основе мультипликативной модели. Прогноз по мультипликативной модели представлен в табл. 2.9 Таблица 2.9 - Прогноз по мультипликативной модели
Прогноз результатов валовой добавленной стоимости по ВЭД Сельское, лесное хозяйство, охоту, рыболовству и рыбоводству по мультипликативной модели составил 467,6 для первого квартала 2019 года и 653,3 для второго квартала 2019 года. Фактически значения данного показателя в анализируемых кварталах составили 506,2 и 691 соответственно. Таким образом, ошибки прогноза составили 7,64% для первого квартала и 5,46% для второго квартала 2019 года. Прогноз по аддитивной модели представлен в табл. 2.10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||