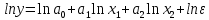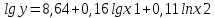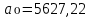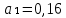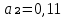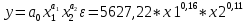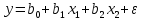Таблица 1.7- Вывод остатков
Наблюдение
|
Предсказанное (Y)=lny
|
Остатки
|
1
|
10,83
|
0,13
|
2
|
10,77
|
-0,26
|
3
|
10,82
|
-0,34
|
4
|
10,96
|
-0,16
|
5
|
10,71
|
-0,14
|
6
|
10,78
|
0,07
|
7
|
10,61
|
-0,03
|
8
|
10,76
|
-0,11
|
9
|
10,76
|
-0,05
|
10
|
11,35
|
0,04
|
11
|
10,67
|
-0,07
|
12
|
10,78
|
-0,10
|
13
|
10,72
|
-0,13
|
14
|
10,73
|
-0,19
|
15
|
10,82
|
-0,06
|
16
|
10,85
|
0,07
|
17
|
10,79
|
0,10
|
18
|
11,48
|
0,75
|
19
|
10,63
|
0,24
|
20
|
10,73
|
0,09
|
21
|
10,81
|
0,23
|
22
|
10,79
|
-0,13
|
23
|
10,76
|
0,11
|
24
|
10,95
|
0,04
|
25
|
10,60
|
0,12
|
26
|
10,60
|
-0,04
|
27
|
11,27
|
0,43
|
28
|
10,47
|
0,09
|
29
|
10,42
|
-0,13
|
30
|
10,78
|
0,33
|
31
|
11,18
|
-0,31
|
32
|
10,73
|
0,05
|
33
|
10,97
|
-0,22
|
34
|
11,10
|
-0,25
|
35
|
10,44
|
0,72
|
36
|
10,88
|
-0,44
|
37
|
10,24
|
0,34
|
38
|
10,62
|
-0,56
|
39
|
10,45
|
0,10
|
40
|
10,58
|
-0,11
|
41
|
10,61
|
0,14
|
42
|
10,98
|
-0,35
|
Построим модель данного вида
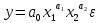 , ,
с использованием метода линерализации
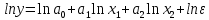
Исходя из результатов анализа, представленных в таблице 1.6, уравнение в преобразованных переменных будет выглядеть следующим образом:
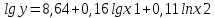
Данное уравнение получаем в естественном виде:
Находим α₀ с использованием формулы «Excel» - формула «EXP» (ЭКСПОНЕНТА)
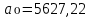
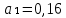
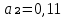
модель имеет следующий вид:
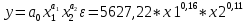
Множественный R = 0,68, это означает, что связь прямая и тесная.
R2 = 68% вариации логарифма Средних цен на первичном рынке жилья на конец года объяснено вариацией логарифма Среднегодовой численности населения и логарифма объема жилищных кредитов, предоставленных кредитными организациями физ лицам в рублях.
Проверка гомоскедастичности остатков для модели 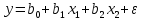
H0 остатки гомоскедастичны.
Таблица 1.8 - выделение подвыборок для теста Гольфреда-Квандта (х₁)
(Y)
|
(X1)
|
(X2)
|
29626
|
271,9
|
5365
|
70195
|
446,2
|
3011
|
38843
|
458,9
|
4103
|
38449
|
465,6
|
3292
|
39489
|
502,2
|
397
|
45223
|
598,4
|
9337
|
52523
|
616,1
|
11264
|
38695
|
627,9
|
8439
|
39381
|
635,3
|
9168
|
35099
|
698,1
|
5984
|
40021
|
736,5
|
12320
|
50023
|
825,4
|
19411
|
23254
|
867,3
|
6120
|
39606
|
938,6
|
14315
|
39229
|
1000,7
|
12221
|
51363
|
1006
|
22749
|
52513
|
1007,3
|
18366
|
47991
|
1009,9
|
13682
|
37855
|
1011,4
|
14053
|
42011
|
1105,5
|
15838
|
43401
|
1111,5
|
20386
|
62346
|
1140,3
|
26500
|
44741
|
1141,7
|
15812
|
42296
|
1164,1
|
19696
|
36884
|
1196,3
|
16821
|
53475
|
1256,5
|
18200
|
47340
|
1265
|
23912
|
35524
|
1362,1
|
21384
|
46592
|
1467,8
|
2568
|
55148
|
1472,5
|
25645
|
57818
|
1548,3
|
19733
|
59035
|
1861,8
|
45525
|
66490
|
1912,2
|
8852
|
49010
|
2326
|
36490
|
46257
|
2499,3
|
34769
|
41156
|
2799,4
|
32461
|
34382
|
3098,5
|
11715
|
51664
|
4200,1
|
59165
|
120600
|
5391
|
195015
|
52552
|
5661,8
|
77706
|
88486
|
7645,2
|
242590
|
203190
|
12646,7
|
393629
|
С помощью инструмента Excel «Регрессия» получим регрессионный анализ, представлен в таб. 1.9 и 1.10
|
 Скачать 152.32 Kb.
Скачать 152.32 Kb.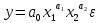 ,
,