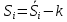эконометрика. Контрольная работа по дисциплине Эконометрика

• Название: Контрольная работа по дисциплине Эконометрика
• Анкор: эконометрика
• Дата: 09.06.2022
• Размер: 152.32 Kb.
• Имя файла: EKONOMETRIKA.docx
• Тип: Контрольная работа; #581723
• страница: 8 из 11

Рисунок 2.4 - Исходный и выровненный ряды

Выравнивание уровней ряда проводится методом скользящей средней.

Для расчёта сезонной компоненты S используем оценки S_i. В аддитивной модели сумма значений сезонной компоненты по всем кварталам равна 0.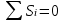



Результат расчётов представим в табл. 2.4

Таблица 2.4 - Расчёт значений сезонной компоненты в аддитивной модели

показатель	год	кварталы
оценка сезонной компоненты для каждого квартала		1	2	3	4
	1	-	-	541,0	93,9
	2	-402,1875	-227,675	543,9	79,925
	3	-391,775	-217,888	542,075	38,45
	4	-379,1625	-227,838	-	-
итоги за i-й квартал		-1173,2	-673,38	1626,94	212,38
средняя оценка сезонной компоненты да и-го квартала,	х	-391,07	-224,46	542,31	70,79
скоректирован сезонная компонента,	х	-390,46	-223,85	542,92	71,4

Корректирующий коэффициент k для данной модели рассчитывается по формуле :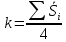

,

где k — корректирующий коэффициент,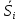

— средняя оценка сезонной компоненты для i-ого квартала.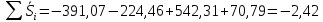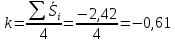





Рассчитаем скорректированные оценки S_i следующим образом.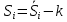



Расчеты скорректированной оценки приведены в табл. 2.4.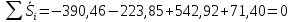



Их сумма равна 0, что соответствует условиям расчета сезонной компоненты для аддитивной модели.

Произведем выравнивание значений сезонной компоненты (табл. 2.5)

Таблица 2.5 - Расчет выровненных значений T и ошибок E в аддитивной модели

t	yt	Si	(T+E)	T	T+S	E=yt-(T+S)	E²
1	388,7	-390,5	779,2	786,1	395,7	-6,9	48,2
2	571,7	-223,9	795,6	792,1	568,2	3,5	12
3	1 349,10	542,9	806,2	798,1	1341	8,1	65,9
4	908,5	71,4	837,1	804	875,4	33,1	1 094,10
5	417,6	-390,5	808	810	419,6	-2	4
6	594,4	-223,9	818,3	816	592,1	2,3	5,1
7	1 368,20	542,9	825,3	822	1364,9	3,3	10,9
8	907,7	71,4	836,3	828	899,3	8,3	69,5
9	436,2	-390,5	826,7	833,9	443,5	-7,3	52,8
10	603,6	-223,9	827,4	839,9	616	-12,5	155,2
11	1 360,60	542,9	817,6	845,9	1388,8	-28,2	797,6
12	863,4	71,4	792	851,9	923,2	-59,8	3 577,80
13	456,8	-390,5	847,2	857,8	467,4	-10,6	112,7
14	634,4	-223,9	858,2	863,8	639,9	-5,6	30,9
15	1 417,90	542,9	875	869,8	1412,7	5,2	27,3
16	1 016,30	71,4	944,9	875,8	947,1	69,1	4 776,60

Для определения компоненты Т данной модели рассчитаем параметры линейного тренда T=a + bt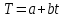



где 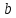— коэффициент регрессии,

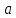— константа.

Находим параметры трендовой компоненты с использованием статистической функции Excel ЛИНЕЙН: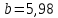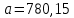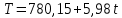






Оцениваем качество построения модели путем расчета квази R²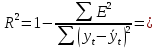

0,9996

Данное значение квази R² свидетельствует, что аддитивная модель объясняет 99,96% общей вариации уровней исследуемого временного ряда за анализируемые 16 кварталов.

График аддитивной модели представлен на рис. 2.5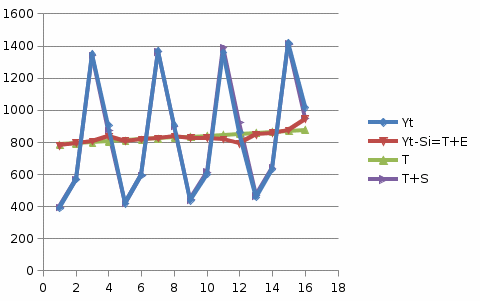



Рисунок 2.5 - Соответствие результатов моделирования исходным данным для аддитивной модели.

Видно, что рассчитанные значения T*S почти не отличаются от фактических значений. Это подтверждает, что в мультипликативной модели доля объясненной вариации уровней очень высокая.

Таким образом, можно сделать вывод, что мультипликативная модель является лучшей, т.к. объясняет больший процент вариации уровней временного ряда.

Производим оценку сезонной компоненты в мультипликативной модели (табл. 2.6)

Таблица 2.6 - Оценки сезонной компоненты для мультипликативной модели.

t	yt	4-хзвенные скользящие средние	центрированные скользящие средние	Оценки сезонной компоненты
1	2	3	4	5
1	388,7	-	-	-
2	571,7	804,5	-	-
3	1349,1	811,7	808,1	1,7
4	908,5	817,4	814,6	1,1
5	417,6	822,2	819,8	0,5
6	594,4	822	822,1	0,7
7	1368,2	826,6	824,3	1,7
8	907,7	828,9	827,8	1,1
9	436,2	827	828	0,5
10	603,6	815,9	821,5	0,7
11	1360,6	821,1	818,5	1,7
12	863,4	828,8	824,9	1
13	456,8	843,1	836	0,5
14	634,4	881,3	862,2	0,7
15	1417,9	-	-	-
16	1016,3	-	-	-

Для расчёта сезонной компоненты S используем оценки S_i. В мультипликативной модели сумма значений сезонной компоненты по всем кварталам равна 4.