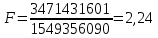Таблица 1.9 – Регрессионный анализ
Регрессионная статистика
|
|
|
|
|
|
|
|
Множественный R
|
0,38
|
|
|
|
|
|
|
|
R-квадрат
|
0,15
|
|
|
|
|
|
|
|
Нормированный R-квадрат
|
0,03
|
|
|
|
|
|
|
|
Стандартная ошибка
|
10163,19
|
|
|
|
|
|
|
|
Наблюдения
|
18,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
Регрессия
|
2
|
267927746,4
|
133963873,2
|
1,2969634
|
0,302317716
|
|
|
|
Остаток
|
15
|
1549356090
|
103290406
|
|
|
|
|
|
Итого
|
17
|
1817283836
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
44634,87
|
8467,68
|
5,27
|
0,00
|
26586,45
|
62683,30
|
26586,45
|
62683,30
|
Переменная X 1
|
-16,60
|
17,01
|
-0,98
|
0,34
|
-52,85
|
19,66
|
-52,85
|
19,66
|
Переменная X 2
|
1,00
|
0,64
|
1,56
|
0,14
|
-0,36
|
2,36
|
-0,36
|
2,36
|
Таблица 1.10 – Регрессионный анализ
Регрессионная статистика
|
|
|
|
|
|
|
|
Множественный R
|
0,94
|
|
|
|
|
|
|
|
|
R-квадрат
|
0,88
|
|
|
|
|
|
|
|
|
Нормированный R-квадрат
|
0,86
|
|
|
|
|
|
|
|
|
Стандартная ошибка
|
15212,78
|
|
|
|
|
|
|
|
|
Наблюдения
|
18,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
Регрессия
|
2
|
24310053355
|
12155026678
|
52,521674
|
1,68131E-07
|
|
|
|
Остаток
|
15
|
3471431601
|
231428773,4
|
|
|
|
|
|
Итого
|
17
|
27781484956
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
42713,59
|
7227,61
|
5,91
|
0,00
|
27308,30
|
58118,88
|
27308,30
|
58118,88
|
Переменная X 1
|
-3,45
|
4,15
|
-0,83
|
0,42
|
-12,29
|
5,40
|
-12,29
|
5,40
|
Переменная X 2
|
0,46
|
0,12
|
3,86
|
0,00
|
0,21
|
0,71
|
0,21
|
0,71
|
Расчет значения F следующим образом:
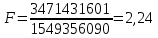
Расчет знамения Fкритич с помощью функции Excel «F.ОБР.ПХ»
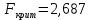
|
 Скачать 152.32 Kb.
Скачать 152.32 Kb.