Химия экзаменационные вопросы. Закон Авогадро. В равных vах всех газов при одинаковых давлении и температуре содержится одинаковое число молекул
 Скачать 186.14 Kb.
|
|
1. Основные газовые законы. Определение молекулярных масс газообразных веществ. К осн. газовому з. относится уравнение состояния газа (уравнение Менделеева-Клапейрона): 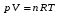 [R – универс. газ. const; n- кол-во в-ва(m/M)]. Газ, который подчиняется этому закону, называется идеальным. Закон Авогадро. В равных V-ах всех газов при одинаковых давлении и температуре содержится одинаковое число молекул. Следствие1: одинаковое число молекул различных газов при одинаковых усл-х занимают одинаковый объем В одном моле содержится  При норм.усл. моль газа занимает 22,4 л.Универсальный газовый з. Для опр. отн. молекулярной массы в-ва обычно находят численно равную ей мольную массу в-ва. Единица молекулярной массы - 1/12 часть массы молекулы углерода, условно принятой равной 12. Масса газообразных веществ опр.поз.Авогадро и уравнению Менделеева-Клапейрона. Основные газовые законы. Определение молекулярных масс газообразных веществ. Основные газовые законы Закон Бойля — Мариотта : при T= const давление газа обратно пропорционально объему газа: Р2/Р1 = V1/V2 или PV = const. Закон Гей - Люссака: при Р=const объем газа изменяется прямо пропорционально абсолютной температуре : V1/T1 = V2/T2 или V/T = const. При V=const давление газа изменяется прямо пропорционально абсолютной температуре: Р1/Т1=P2/Т2. Объединяя эти законы, получим универсальный газовый закон: PV/T = const. ОПРЕДЕЛЕНИЕ МОЛЕКУЛЯРНЫХ МАСС ГАЗООБРАЗНЫХ ВЕЩЕСТВ Если температура и давление отличаются от нормальных; то молекулярную массу газообразных веществ удобно вычислять с помощью уравнения Менделеева-Клапейрона, представляющего собой математическое выражение зависимости между объемом газа, его весом, молекулярной массой, давлением и температурой: pV=(m/M)RT 2. Основные стехиометрические законы 1. Закон постоянства состава Всякое химически чистое соединение независимо от способа его получения имеет вполне определенный состав. На основании этого закона состав веществ выражается химической формулой с помощью химических знаков и индексов. Закон постоянства состава справедлив для веществ молекулярного строения. Наряду с веществами, имеющими постоянный состав, существуют вещества переменного состава. К ним относятся соединения, в которых чередование нераздельных структурных единиц (атомов, ионов) осуществляется с нарушением периодичности. В связи с наличием соединений переменного состава современная формулировка закона постоянства состава содержит уточнения: Состав соединений молекулярного строения, то есть состоящих из молекул, является постоянным независимо от способа получения. Состав же соединений с немолекулярной структурой (с атомной, ионной и металлической решеткой) не является постоянным и зависит от условий получения. Пример: 2H2+O2=2H2O и 4NH3+3O2=6H2O+2N. 2. 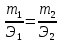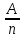Закон эквивалентов:  (m- масса; Э-эквивалент).Э =  (A-масса 1 моля в-ва, n-его валентность).Хим.эквивалент - такое весовое кол-во в-ва, которое реагирует с 1.008 весовых частей H2 или 8 в.ч. О2. 3. Закон простых кратных отношений: Если два элемента образуют между собой несколько молекулярных соединений, то масса одного элемента, приходящаяся на одну и ту же массу другого, относятся между собой как небольшие целые числа. К. о. з. открыт в 1803 Дж. Дальтоном и истолкован им с позиций атомизма. Пример: H2O/H2O2 , CO/CO2, N2O/NO/N2O3/NO2/N2O4/N2O5. 4. Закон сохранения массы: Масса веществ, вступивших в химическую реакцию, равна массе веществ, образующихся в результате реакции. Закон сохранения массы веществ является основным законом химии, все расчеты по химическим реакциям производятся на его основе. Закон сохранения массы был теоретически открыт в 1748 году и экспериментально подтверждён в 1756 году русским ученым М.В. Ломоносовым. Французский учёный Антуан Лавуазье в 1789 году окончательно убедил учёный мир в универсальности этого закона. 5. Закон Авогадро: в равных объемах всех газов при одинаковых давлении и температуре содержится одинаковое число молекул. В одном моле содержится 3. Закон химических эквивалентов. Молярные массы эквивалентов сложных веществ. * Закон эквивалентов - Все вещества реагируют и образуются в эквивалентных соотношениях. - Вещества взаимодействуют друг с другом в количествах, пропорциональных их эквивалентам. - Массы (объёмы) реагирующих друг с другом веществ пропорциональны их эквивалентным массам (объемам). Формула, выражающая Закон эквивалентов: m1Э2=m2Э1 Закон эквивалентов для окислительно-восстановительной реакции: 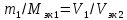 Эквивалентом элемента называют такое его количество, которое соединяется с 1 молем атомов водорода или замещает то же количество атомов водорода в химических реакциях. Эквивалент – реальная частица (атом, молекула, ион) или условная частица (доля атома, молекулы, иона), равноценная одному иону водорода в кислотно-основных реакциях или одному электрону в окислительно-восстановительных реакциях (Обозначается Э). Масса 1 эквивалента называется его эквивалентной массой. Эквивалент можно вычислить по составу соединения данного элемента с любым другим, эквивалент которого известен. Оксиды: Мэк = М(оксида) / (n(Me)*(c.o. Me)) Основания: Мэк = М(основания) / кол-во ОН-групп Кислоты: Мэк = М(кислоты) / кол-во Н Соли: Мэк = М(соли) / (n(Me)*(c.o. Me)) Металл-восстановитель: 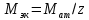 4. Волновые свойства электрона. Квантовые числа … - состояния электрона. Электронные орбитали. Проскок электрона. В 20-х годах XX столетия было установлено, что любая частица имеет корпускулярно-волновую природу. Согласно теории Л. де Бройля (1924 г.), каждой частице с импульсом 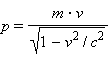 соответствует волновой процесс с длиной волны λ, т.е. λ = h / p. Чем меньше масса частицы, тем больше длина волны. Для элементарных частиц В. Гейзенберг сформулировал принцип неопределенности, согласно которому невозможно одновременно определить положение частицы в пространстве и ее импульс. Следовательно, нельзя рассчитать траекторию движения электрона в поле ядра, можно лишь оценить вероятность его нахождения в атоме с помощью волновой функции ψ, которая заменяет классическое понятие траектории. Волновая функция ψ характеризует амплитуду волны в зависимости от координат электрона, а ее квадрат ψ2 определяет пространственное распределение электрона в атоме. В наиболее простом варианте волновая функция зависит от трех пространственных координат и дает возможность определить вероятность нахождения электрона в атомном пространстве или его орбиталь. Таким образом, атомная орбиталь (АО) – область атомного пространства, в котором вероятность нахождения электрона наибольшая.Волновые функции получаются при решении основополагающего соотношения волновой механики – уравнения Шредингера. Точное решение существует для атома водорода или водородоподобных ионов, для многоэлектронных систем используются различные приближения. Поверхность, ограничивающая 90–95 % вероятности нахождения электрона или электронной плотности, называют граничной. Атомная орбиталь и плотность электронного облака имеют одинаковую граничную поверхность (форму) и одинаковую пространственную ориентацию. Атомные орбитали электрона, их энергия и направление в пространстве зависят от четырех параметров – квантовых чисел. 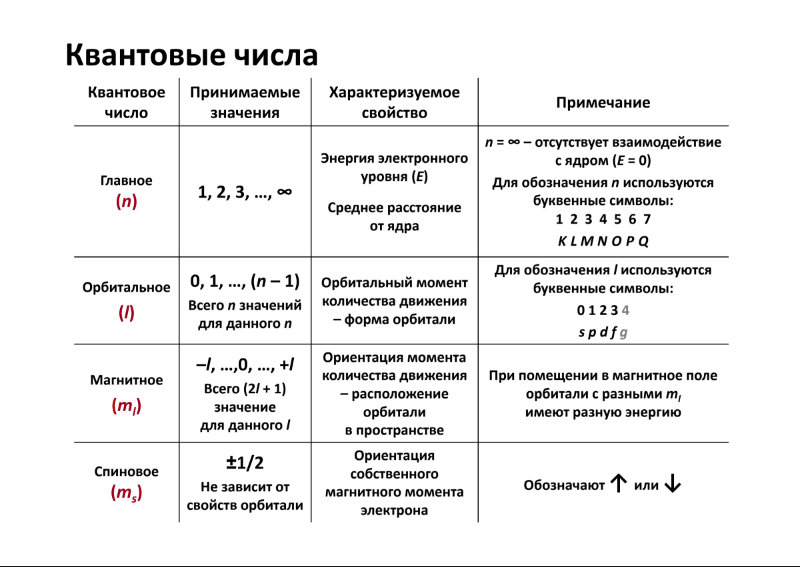 Французский физик Л. де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами. Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота ν и длина волны λ. Согласно гипотезе де Бройля (1924), электрон (как и все другие материальные микрообъекты) обладает не только корпускулярными, но и волновыми свойствами. В соответствии с этим электроны, подобно свету, могут испытывать интерференцию и дифракцию. Дифракция - явления, наблюдаемые при прохождении волн мимо края препятствия, связанные с отклонением волн от прямолинейного распространения при взаимодействии с препятствием интерференция - сложение в пространстве двух (или нескольких) волн, при котором в разных точках получается усиление или ослабление амплитуды результирующей волны 1. В многоэлектронном атоме подуровни имеют различную энергию. Для одноэлектронного приближения их распределение по энергиям показано далее... 2. Зависимость энергии орбитали от заряда ядра носит сложный немонотонный характер: • с ростом Z энергии всех орбиталей понижаются; • в пределах одного периода разница энергий подуровней (ΔEs‐p) возрастает; • при заполнении электронами d и f орбиталей их расположение по сравнению с одноэлектронным приближением существенно изменяется. Принцип наименьшей энергии В многоэлектронном атоме стабильной является такая конфигурация, для которой достигается минимум полной энергии. В первую очередь заполняются орбитали с наименьшей энергией, т.е. выполняется последовательность: 1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 6d < 5f Энергия орбиталей увеличивается в порядке возрастания суммы квантовых чисел (n +l), а при одинаковой сумме этих чисел – в порядке возрастания главного квантового числа. Электронная орбиталь - это область наиболее вероятного местонахождения электрона в пространстве. Проскок электрона — отступления от общей для большинства элементов последовательности заполнения электронных оболочек, связанные с тем, что эти “нарушения правил” обеспечивают атомам некоторых элементов меньшую энергию по сравнению с заполнением электронных оболочек “по правилам”. Объясняется это тем, что энергетически более выгодно, когда в атоме имеется наполовину или полностью заполненный подуровень (р3; р6; d5; d10; f7; f14). Поэтому в атомах элементов, у которых строение электронной оболочки близко к вышеуказанному, может наблюдаться преждевременное заполнение d- подуровня за счёт проскока (или провала) электрона с внешнего s- подуровня на нижележащий (предвнешний) d- подуровень (закономерные проскоки)
5. Принцип Паули. Емкость энергетических уровней и подуровней атомов элемента. Правило Хунда. Принцип запрета Паули: В атоме не существует двух электронов, состояние которых описывается одинаковым набором квантовых чисел (n, l, ml, ms). Следовательно, на одной орбитали (она характеризуется тремя квантовыми числами (n, l, ml)) может находиться не более двух электронов с разными значениями спинового квантового числа (↑ и ↓) Правило Хунда: суммарный спин данного подуровня должен быть максимальным, т.е. электроны стремятся занять максимальное число свободных квантовых состояний Электронная ёмкость энергетического подуровня определяется числом атомных орбиталей в подуровне и, исходя из ёмкости каждой АО, численно равна 2(2l+1), а именно: Энергетический подуровень s p d f Число АО в подуровне (2l+1) 1 3 5 7 Электронная ёмкость подуровня 2(2l+1) 2 6 10 14 Электронная ёмкость энергетического уровня определяется ёмкостью составляющих его энергетических подуровней и численно равна 2n2, где n – значение главного квантовогочисла для электронов рассматриваемого энергетического уровня 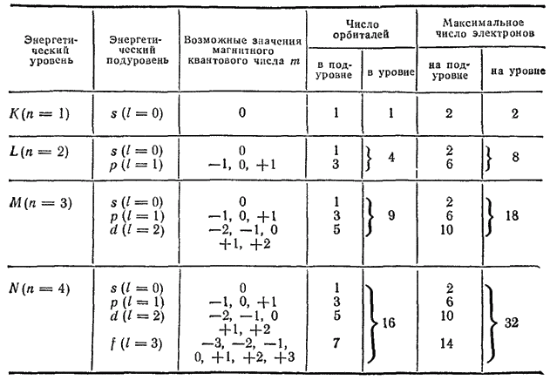 | ||||||||||||||||||||